Файл: Реферат применение формулы Байеса в профессии и в экономике студент группы 38. 03. 02.rtf
Добавлен: 30.11.2023
Просмотров: 138
Скачиваний: 3
СОДЕРЖАНИЕ
Основные понятия и определения
Введение в байесовские сети доверия.
Моделирование в условиях неопределенности
Экспертные системы и формальная логика
Особенности вывода суждений в условиях неопределенности
Использование Байесовых сетей.
Вероятности прогнозируемых значений отдельных переменных
Пример построения простейшей байесовской сети доверия.
Байесовские сети доверия как одно из направлений современных экспертных систем.
Представление знаний с использованием байесовской сети доверия и условная независимость событий.
Замечание о субъективных вероятностях и ожидания.
Синтез сети на основе априорной информации.
Пример использования Байесовых сетей
Космические и военные применения
Компьютеры и системное программное обеспечение
AUAI — Ассоциация анализа неопределенности в искусственном интеллекте
где p(ek|ci, dj) – вероятность пребывания в состоянии ek в зависимости от состояний ci, dj. Так как события, представленные вершинами «c» и «d» независимы, то
p(ek |ci , dj) = p(ci) *p(dj).

Рис.2. Двухуровневая БСД.
Рассмотрим пример более сложной сети (рис.2). Данный рисунок иллюстрирует условную независимость событий. Для оценки вершин «c» и «d» используются те же выражения, что и для вычисления p(ek), тогда:
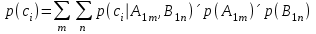 ,
,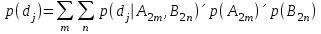 .
.Из этих выражений видно, что вершина «e» условно не зависит от вершин A1, A2, B1, B2, так как нет стрелок непосредственно соединяющих эти вершины.
Рассмотрев эти примеры попробуем теперь более точно определить основные понятия, используемые в БСД. Байесовские сети доверия — это направленный ациклический граф, обладающий следующими свойствами:
1.каждая вершина представляет собой событие, описываемое случайной величиной, которая может иметь несколько состояний;
2.все вершины, связанные с “родительскими” определяются таблицей условных вероятностей (ТУВ) или функцией условных вероятностей (ФУВ);
3.для вершин без “родителей” вероятности её состояний являются безусловными ( маргинальными).
Другими словами, в байесовских сетях доверия вершины представляют собой случайные переменные, а дуги – вероятностные зависимости, которые определяются через таблицы условных вероятностей. Таблица условных вероятностей каждой вершины содержит вероятности состояний этой вершины при условии состояний её “родителей”.
Моделирование в условиях неопределенности
Экспертные системы и формальная логика
Попробуем проследить за способом работы эксперта в некоторой определенной области. Примерами экспертов являются врач, проводящий обследование, финансист, изучающий условия предоставления ссуды, либо пилот, управляющий самолетом.
Действия эксперта могут условно быть представлены в виде повторяющейся последовательности из трех этапов:
1.получение информации о состоянии окружающего мира;
2.принятие решения относительно выбора некоторых действий, по поводу которых у эксперта имеются определенные ожидания последствий;
3.приобретение опыта путем сопоставления результатов действий и ожиданий и возврат к первому этапу.
Приобретенный новый опыт и информация о мире позволяют эксперту сообразно действовать в будущем. Попытки компьютерного моделирования действий эксперта привели в конце 60-х годов к появлению экспертных систем (ЭС) , которые чаще всего основывались на продукционных правилах типа «ЕСЛИ условие, ТО факт или действие». Будущее подобных систем связывалось при этом с заменой экспертов их моделями. Однако после первых успехов обнажились проблемы, и первой среди них — серьезные затруднения при попытках работы с нечеткой, недоопределенной информацией.
Следующие поколения ЭС претерпели кардинальные изменения:
-
вместо моделирования эксперта моделируется предметная область; -
вместо попыток учета неопределенности в правилах — использование классической теории вероятностей и теории принятия решений; -
вместо попыток замены эксперта — оказание ему помощи.
В конце 80-х годов были предложены обобщения ЭС в виде байесовых сетей, и была показана практическая возможность вычислений вероятностных выводов даже для сетей больших размеров. Вернемся к трехэтапному описанию профессиональных действий эксперта. Сейчас нас будет интересовать вопрос, как наблюдения эксперта, т. е. получение им информации о внешнем мире, изменяют его ожидания по поводу ненаблюдаемых событий?
Особенности вывода суждений в условиях неопределенности
Суть приобретаемого знания в условиях неопределенности состоит в понимании, влияет ли полученная информация на наши ожидания относительно других событий. Основная причина трудностей при использовании систем, основанных на правилах, состоит в учете «сторонних», «косвенных» последствий наблюдаемых событий. Проиллюстрируем это на уже успевшем стать классическим примере.
Шерлок Холмс вышел из дома утром и заметил, что трава вокруг влажная. Он рассудил: «Я думаю, что ночью был дождь. Следовательно, трава возле дома моего соседа, доктора Ватсона, вероятно, также влажная». Таким образом, информация о состоянии травы у дома Холмса повлияла на его ожидания относительно влажности травы у дома Ватсона. Но предположим, что Холмс
проверил состояние сборника дождевой воды и обнаружил, что тот - сухой. В результате Холмс вынужден изменить ход своих рассуждений, и состояние травы возле его дома перестает влиять на ожидания по поводу травы у соседа.
Теперь рассмотрим две возможные причины, почему трава у дома Холмса оказалась влажной. Помимо дождя, Холмс мог просто забыть выключить поливальную установку накануне.
Допустим, на следующее утро Холмс снова обнаруживает, что трава влажная. Это повышает его субъективные вероятности и для прошедшего дождя, и по поводу забытой дождевальной установки. Затем Холмс обнаруживает, что трава у дома Ватсона также влажная и заключает, что ночью был дождь.
Следующий шаг рассуждений практически невозможно воспроизвести в системах, основанных на правилах, однако он абсолютно естественен для человека: влажность травы у дома Ватсона объясняется дождем, и следовательно нет оснований продолжать ожидать, что была забыта включенной поливальная машина. Следовательно, возросшая, было, субъективная вероятность относительно забытой поливальной машины уменьшается до (практически) исходного значения, имевшего место до выхода Холмса из дома. Такой способ рассуждения можно назвать «попутное объяснение», «контекстное объяснение» или «редукция причины» (explaining away).
Важная особенность «попутного объяснения» состоит в изменении отношений зависимости между событиями по мере поступления информации. До выхода из дома Холмса факты дождя и работы поливальной установки были независимы. После получения информации о траве у дома они стали зависимыми. Далее, когда появилась информации о влажности травы у дома Ватсона, состояние зависимости вновь изменилось.
Эту ситуацию удобно описать при помощи графа, узлы которого представляют события (или переменные), а пара узлов (A, B) связывается направленным ребром, если информация об A может служить причиной для B. В этом случае узел A будет родителем для B, который, в свою очередь, называется узлом-потомком по отношению к A.
История с травой у Холмса и Ватсона представлена на рис. 1.
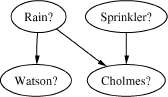
Рисунок 1 Граф рассуждений Шерлока Холмса
Граф на рис. 1 может быть отнесен к семейству байесовых сетей. В данном примере переменные в узлах могут принимать только булевы значения 1 или 0 (да/нет). Из графа на рис. 1 можно сделать несколько полезных выводов о зависимости и независимости переменных. В традиционной постановке байесовы сети не предназначены для оперирования с непрерывным набором состояний (например, с действительным числом на заданном отрезке). Для представления действительных чисел в некоторых приложениях можно провести разбиение отрезка на сегменты и рассматривать дискретный набор их центров.
Например, если известно, что ночью не было дождя, то информация о состоянии травы у дома Ватсона не оказывает влияния на ожидания по поводу состояния травы у дома Холмса.
В середине 80-х годов были подробно проанализированы способы, которыми влияние информации распространяется между переменными в байесовой сети. Будем считать, что две переменные разделены, если новые сведения о значении одной из них не оказывают влияния на ожидания по поводу другой. Если состояние переменной известно, мы будем называть такую переменную конкретизированной.
В байесовой сети возможны три типа отношений между переменными:
1.последовательные соединения (рис. 2a);
2.дивергентные соединения (рис. 2b),;
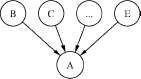
3.конвергентные соединения (рис. 2c).
Ситуация на рис. 2c требует, по-видимому, дополнительных пояснений—как возникает
зависимость между предками конвергентного узла, когда становится известным значение потомка.
Для простоты рассмотрим пример, когда узел A имеет всего двух предков –B и C. Пусть эти две
переменные отвечают за выпадение орла и решки при независимом бросании двух разных монет, а
переменная A — логический индикатор, который «загорается», когда обе монеты оказались в
одинаковом состоянии (например, обе - решки). Теперь легко понять, что если значение
индикаторной переменной стало известным, то значения B и C стали зависимыми — знание одного
из них полностью определяет оставшееся.
Общее свойство (условной) независимости переменных — узлов в байесовой сети получило
название d-разделения (d-separation).
Определение d-разделимости
Две переменные A и B в байесовой сети являются d-разделенными, если на каждом пути,
соединяющем эти две вершины на графе, найдется промежуточная переменная V, такая что:
-
соединение с V последовательное или дивергентное и значение V известно, либо -
соединение конвергентное и нет свидетельств ни о значении V, ни о каждом из ее потомков.
Так, в сети задачи Шерлока Холмса (рис. 1) переменные «Полив?» и «Трава у дома Ватсона?»
являются d-разделенными. Граф содержит на пути между этими переменными конвергентное
соединение с переменной «Трава у дома Холмса?».
(a)
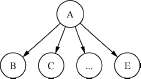
(b)
(c)Рисунок 2 Три типа отношений между переменным
и(a) Последовательное соединение. Влияние информации может распространяться от A к C и обратно, пока значение B не конкретизировано. (b) Дивергентное соединение. Влияние может распространяться между потомками узла A, пока его значение не конкретизировано. (c) Конвергентное соединение. Если об A ничего не известно, кроме того, что может быть выведено из информации о его предках B,C,... ,E, то эти переменные предки являются разделенными. При уточнении A открывается канал взаимного влияния между его предками.
Свойство d-разделимости соответствует особенностям логики эксперта-человека, поэтому крайне желательно, чтобы в рассуждениях машин относительно двух d-разделенных переменных новая информация об одной из них не изменяла степень детерминированности второй переменной. Формально, для переменных A и C, независимых при условии B, имеет место соотношение P(A | B) = P(A | B, C).
Отметим, что интуитивное восприятие условной зависимости и независимости иногда, даже в простых случаях, оказывается затрудненным, так как сложно из всех исходов событий мысленно выделить только те события, в которых значение обусловливающей переменной определено, и далее в рассуждения оперировать только ими.
Вот простой пример, поясняющий эту трудность: в некотором сообществе мужчины среднего возраста и молодые женщины оказались материально более обеспеченными, чем остальные люди. Тогда при условии фиксированного повышенного уровня обеспеченности пол и возраст человека оказываются условно зависимыми друг от друга!