Файл: Реферат применение формулы Байеса в профессии и в экономике студент группы 38. 03. 02.rtf
Добавлен: 30.11.2023
Просмотров: 146
Скачиваний: 3
СОДЕРЖАНИЕ
Основные понятия и определения
Введение в байесовские сети доверия.
Моделирование в условиях неопределенности
Экспертные системы и формальная логика
Особенности вывода суждений в условиях неопределенности
Использование Байесовых сетей.
Вероятности прогнозируемых значений отдельных переменных
Пример построения простейшей байесовской сети доверия.
Байесовские сети доверия как одно из направлений современных экспертных систем.
Представление знаний с использованием байесовской сети доверия и условная независимость событий.
Замечание о субъективных вероятностях и ожидания.
Синтез сети на основе априорной информации.
Пример использования Байесовых сетей
Космические и военные применения
Компьютеры и системное программное обеспечение
AUAI — Ассоциация анализа неопределенности в искусственном интеллекте
Компьютеры и системное программное обеспечение
В фирме Microsoft методики байесовых сетей применены для управления интерфейсными агентами-помощниками в системе Office (знакомая многим пользователям «скрепка»), в диагностике проблем работы принтеров и других справочных и wizard-подсистемах.
Обработка изображений и видео
Важные современные направления применений байесовых сетей связаны с восстановлением трехмерных сцен из двумерной динамической информации, а также синтеза статических изображений высокой четкости из видеосигнала.
Финансы и экономика
В серии работ школы бизнеса Университета штата Канзас описаны байесовы методики оценки риска и прогноза доходности портфелей финансовых инструментов. Основными достоинствами байесовых сетей в финансовых задачах является возможность совместного учета количественных и качественных рыночных показателей, динамическое поступление новой информации, а также явные зависимости между существенными факторами, влияющими на финансовые показатели.
Результаты моделирования представляются в форме гистограмм распределений вероятностей, что позволяет провести детальный анализ соотношений «риск-доходность». Весьма эффективными являются также широкие возможности по игровому моделированию.
Описание прикладных программ
Байесовы сети — интенсивно развивающаяся научная область, многие результаты которой уже успели найти коммерческое применение. Приводится список популярных программ, спектр которых, отражает общую картину, возникшую в последние 10-15 лет.
AUAI — Ассоциация анализа неопределенности в искусственном интеллекте
(URL: http://www.auai.org/)
Ассоциация анализа неопределенности в искусственном интеллекте (Association for Uncertainty in Artificial Intelligence — AUAI) — некоммерческая организация, главной целью которой является проведение ежегодной Конференции по неопределенности в искусственном интеллекте (UAI).
Конференция UAI-2002 прошла в начале августа 2002 года в Университете Альберты (Эдмонтон, Канада). Конференции UAI проходят ежегодно, начиная с 1985 года, обычно в совместно с другими конференциями по смежным проблемам. Труды конференций издаются в виде книг, однако многие статьи доступны в сети.
NETICA
(URL: http://www.norsys.com/index.html)
Norsys Software Corp. — частная компания, Расположенная в Ванкувере (Канада). Norsys специализируется в разработке программного обеспечения для байесовых сетей. Программа Netica —основное достижение компании, разрабатывается с 1992 года и стала коммерчески доступной в 1995 году. В настоящее время Netica является одним из наиболее широко используемых инструментов для разработки байесовых сетей.
Версия программы с ограниченной функциональностью свободно доступна на сайте фирмы Norsys.
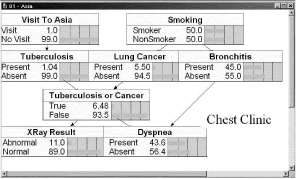
Рисунок 1 Пример байесовой сети в приложении Netica
Netica — мощная, удобная в работе программа для работы с графовыми вероятностными моделями. Она имеет интуитивный и приятный интерфейс пользователя для ввода топологии сети. Соотношения между переменными могут быть заданы, как индивидуальные вероятности, в форме уравнений, или путем автоматического обучения из файлов данных (которые могут содержать пропуски).
Созданные сети могут быть использованы независимо, и как фрагменты более крупных моделей, формируя тем самым библиотеку модулей. При создании сетевых моделей доступен широкий спектр функций и инструментов.
Многие операции могут быть сделаны несколькими щелчками мыши, что делает систему Netica весьма удобной для поисковых исследований, и для обучения и для простого просмотра, и для обучения модели байесовой сети. Система Netica постоянно развивается и совершенствуется.
Knowledge Industries
(URL: http://www.kic.com/)
Knowledge Industries —ведущий поставщик программных инструментальных средств для разработки и внедрения комплексных диагностических систем. При проектировании сложных и дорогостоящих вариантов систем диагностик в компании используется байесовы сети собственной разработки.
Data Digest Corporation
(URL: http://www.data-digest.com/home.html)
Data Digest Corporation является одним из лидеров в применении методов байесовых сетей к анализу данных.
BayesWare, Ltd
(URL: http://www.bayesware.com/corporate/profile.html)
Компания BayesWare основана в 1999 году. Она производит и поддерживает программное обеспечение, поставляет изготовленные на заказ решения, предоставляет программы обучения, и предлагает услуги консультирования корпоративным заказчикам и общественным учреждениям. Одна из успешных разработок компании, Bayesware Discoverer, основана на моделях байесовых сетей.
HUGIN Expert
(URL: http://www.hugin.com/)
Компания Hugin Expert была основана в 1989 году в Ольборге, (Дания). Их основной продукт Hugin начал создаваться во время работ по проекту ESPRIT, в котором системы, основанные на знаниях, использовались для проблемы диагностирования нервно-мышечных заболеваний. Затем началась коммерциализация результатов проекта и основного инструмента — программы Hugin. К настоящему моменту Hugin адаптирована во многих исследовательских центрах компании в 25 различных странах, она используется в ряде различных областей, связанных с анализом решений, поддержкой принятия решений, предсказанием, диагностикой, управлением рисками и оценками безопасности технологий.
Hugin является программой реализацией системы принятия решений на основе байесовских сетей доверия. Имеет две версии Pro и Explorer. Функционирует в среде OS Windows’95, Windows NT, а также имеет версию UNIX. Эта система имеет развитый интерфейс и позволяет достаточно просто создавать базы знаний и фактов. Использует два основных режима работы:
режим редактирования и построения причинно-следственной сети, а также заполнения таблиц условных вероятностей, являющихся количественным описанием БЗ.
режим расчёта вероятностных оценок для принятия решения по всем событиям, входящим в причинно-следственную сеть. Расчёты могут осуществляться как на основе классической теории Байеса, так и на основе методов теории возможностей.
“Hugin” имеет возможность связи с основными наиболее распространёнными программными средствами фирмы Microsoft. Данная ЭС имеет все основные функции
любой информационной системы, включая такие как: хранение данных, вывод на принтер всех элементов ЭС, диагностика ошибок в работе.
Выводы
Байесовы вероятностные методы обучения машин являются существенным шагом вперед, в сравнении с популярными моделями «черных ящиков». Они дают понятное объяснение своих выводов, допускают логическую интерпретацию и модификацию структуры отношений между переменными задачи, а также позволяют в явной форме учесть априорный опыт экспертов в соответствующей предметной области.
Благодаря удачному представлению в виде графов, байесовы сети весьма удобны в пользовательских приложениях.
Байесовы сети базируются на фундаментальных положениях и результатах теории вероятностей, разрабатываемых в течение нескольких сотен лет, что и лежит в основе их успеха в практической плоскости.
Байесова методология, в действительности, шире, чем семейство способов оперирования с условными вероятностями в ориентированных графах. Она включает в себя также модели с симметричными связями (случайные поля и решетки), модели динамических процессов (марковские цепи), а также широкий класс моделей со скрытыми переменными, позволяющих решать вероятностные задачи классификации, распознавания образов и прогнозирования.
В ближайшем будущем предполагается значительно расширить применение Байесовых сетей доверия. Например, на одном из сайтов поисковиков конструируются байесовские сети для моделирования успешных запросов, поступающих от пользователей. Эти сети могут пополнять регистрационный файл поискового сервера назначаемыми категориями предполагаемых целей информации для обеспечения возможности предсказания модификаций запросов.
Заключение
Формула полной вероятности широко использовалась математиками при конкретных расчётах ещё в начале XVIII века, но впервые была сформулирована как одно из основных утверждений теории вероятностей Пьером-Симоном Лапласом лишь в конце того века. Она применяется, в частности, при нахождении среднего выходного уровня дефектности в задачах статистического обеспечения качества продукции.Формула Байеса позволяет «переставить причину и следствие»: по известному факту события вычислить вероятность того, что оно было вызвано данной причиной.События, отражающие действие «причин», в данном случае обычно называют гипотезами, так как они — предполагаемые события, повлекшие данное. Безусловную вероятность справедливости гипотезы называют априорной (насколько вероятна причина вообще), а условную — с учетом факта произошедшего события —
апостериорной (насколько вероятна причина оказалась с учетом данных о событии).
Можно также уточнять вероятность гипотезы, учитывая другие имеющиеся данные (другие произошедшие события). Для учета каждого следующего события нужно в качестве априорной вероятности гипотезы подставлять ее апостериорную вероятность с предыдущего шага.
Литература
-
Вентцель Е.С. Теория вероятностей. - М, «Высшая школа» 2002 -
Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. - М, «Высшая школа» 2004 -
Письменный Д.Т. Конспект лекций по теории вероятностей и математической статистике. – М, «Айрис-пресс» 2004 г. -
Сайт: Численные методы и теория вероятностей. http://www.uchites.ru/ -
Гмурман В. Е. Теория вероятностей и математическая статистика, — М.: Высшее образование.2005. -
Таха Х.А., Введение в исследование операций, Вильямс, Киев, 2005. -
Терехов С.А., Лекции по нейроинформатике, МИФИ, М., 2003. -
Хабаров С., Экспертные системы, M., 2003. -
Чернова Н.И., Математические методы и исследование операций в эк., М., 2000.