Файл: Криволинейный интеграл по плоской кривой (криволинейный интеграл 1 рода).doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 02.12.2023
Просмотров: 95
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
-
Криволинейный интеграл по плоской кривой (криволинейный интеграл 1 рода)
Пусть Г- кривая, лежащая на плоскости хОу. Выясним геометрический смысл криволинейного интеграла
Построим цилиндрическую поверхность с направляющей линией Г и образующими, параллельными оси OZ. В каждой точке Р Г длину образующей сделаем равной значению функции f(P) (рисунок 30).
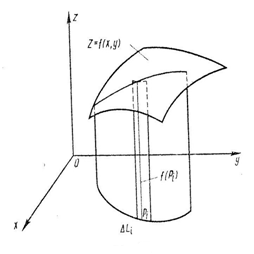
Рисунок 30
Цилиндрическая поверхность пересечена сверху поверхностью z=f(x, у). Найдем площадь S построенной части цилиндрической поверхности. Если разбить линию Г на части
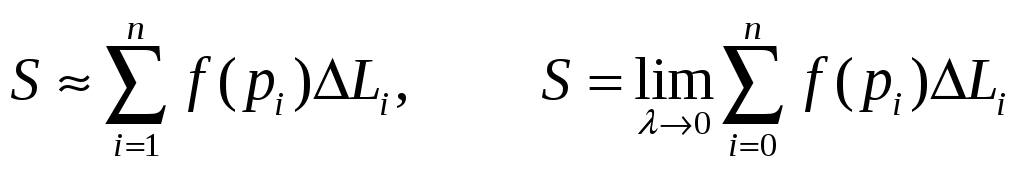
где -наибольший из диаметров частей
Таким образом криволинейный интеграл
1.1 Вычисление криволинейных интегралов
Вычисление криволинейно интеграла сводится к
вычислению обычного определенного интеграла, если воспользоваться выведенными в дифференциальном исчислении формулами для дифференциала длины дуги dL. Рассмотрим сперва плоскую кривую Г, по которой требуется вычислить интеграл
В криволинейном интеграле та функция, которую мы интегрируем, не имеет ничего общего с уравнениями кривой, по которой ведется интегрирование.
Вспомним формулу:
и подставим выражение для dL в наш интеграл. Одновременно, воспользуемся уравнением у =
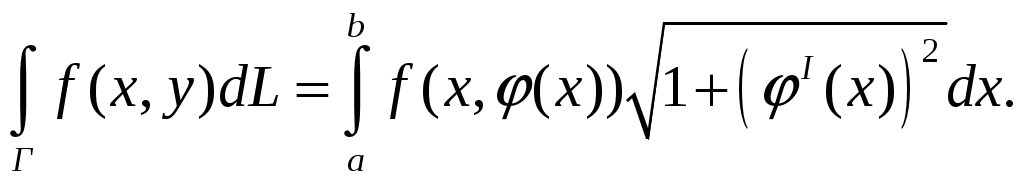 (35)
(35)Справа, в формуле (35), стоит самый обычный определенный интеграл. Если бы кривая Г была задана уравнением: x=(у) , где с ≤ у≤ d, то получили бы,
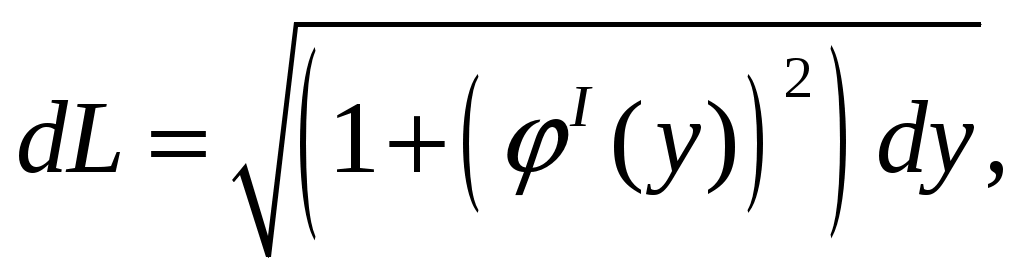 (36)
(36)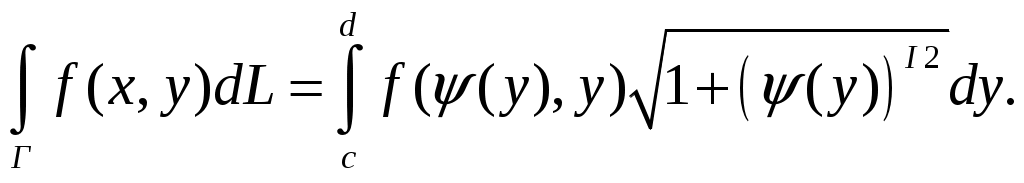 (37)
(37)Если кривая Г задана параметрическими уравнениями х=х(t), у=у(t),
получаем равенство
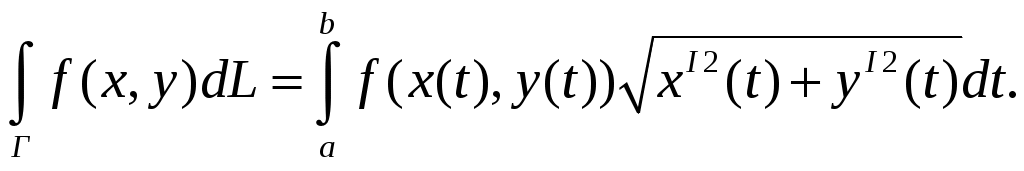 (39)
(39)В правой части стоит обычный определенный интеграл от некоторой функции переменной t.
Точно так же, когда кривая Г пространственная и задана уравнениями
выражение для dL имеет вид
и поэтому
(41)
Наконец, в случае, когда плоская линия Г задана полярным уравнением r=r(
Получим
С
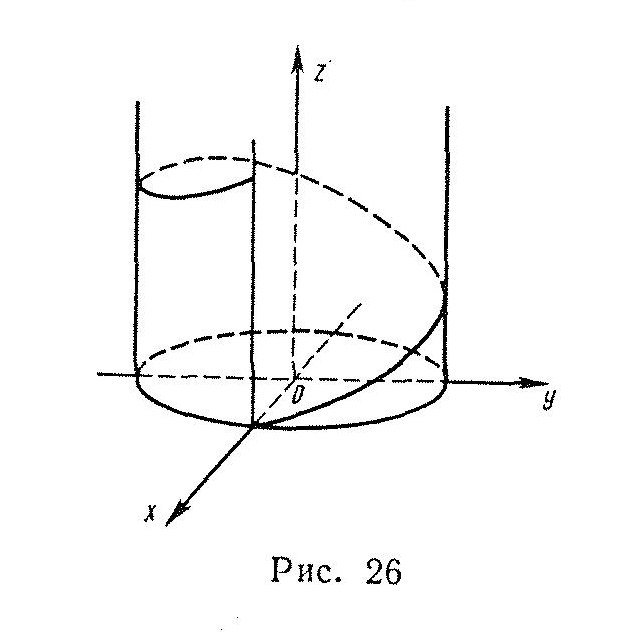
Рисунок 31
ведение криволинейного интеграла к обычному определенному интегралу по идее очень близко к замене переменной в определенном интеграле. Однако, следует иметь в виду одно отличие. После замены переменной в определенном интеграле, может случиться, что нижний предел интегрирования оказывается больше верхнего. При вычислении же криволинейного интеграла всегда нижний предел должен быть меньше верхнего. Это вызывается тем, что элемент dL, длины дуги всегда должен быть больше нуля. Таким образом, при переходе от криволинейного интеграла к обыкновенному определенному интегралу переменная, выбранная в качестве основной, должна пробегать промежуток своего изменения в сторону возрастания.
Примеры 1. Найти длину дуги Г параболы у=х2 на участке от х= 0 до х=а.
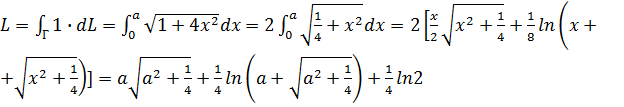 .
.2. Найти массу М одной четверти окружности радиуса a, расположенной в первом квадрате, если плотность
Имеем:
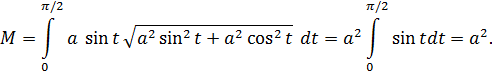
3. Найти длину первого витка винтовой линии (рисунок 31) х=acos t, y = a sin t, z = bt.
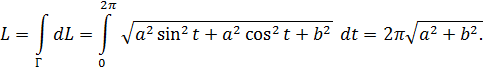
При развертывании цилиндра на плоскость первый виток винтовой линии изобразится диагональю прямоугольника со сторонами 2
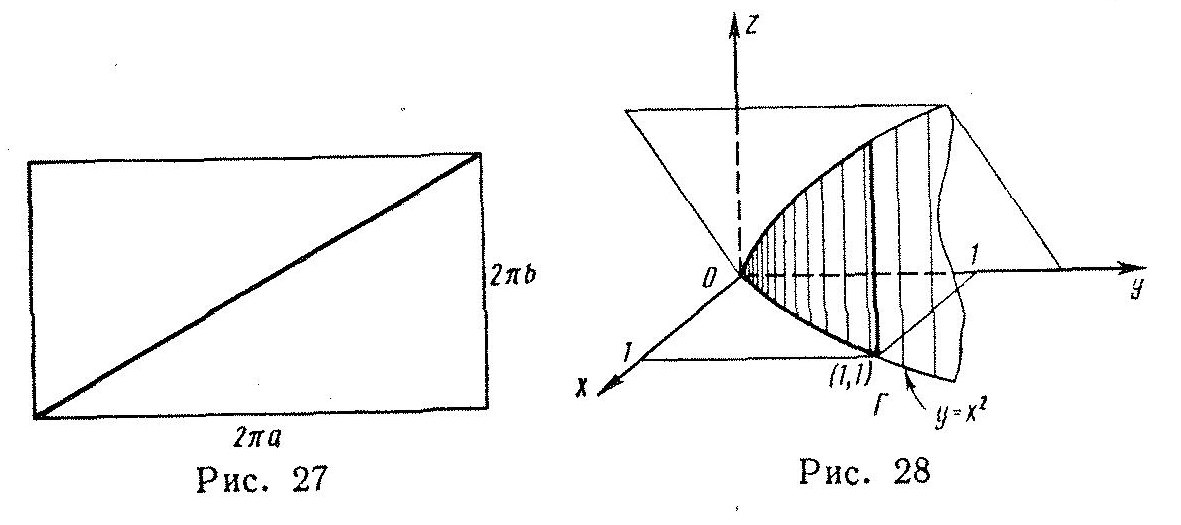
Рисунок 32
Рисунок 33
4. Найти площадь части боковой поверхности цилиндра у= х2, лежащей в первом октанте и вырезанной плоскостями z=х и х=1.
Воспользуемся геометрическим смыслом интеграла
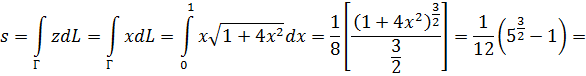
5. Найти длину первого витка спирали Архимеда r = a
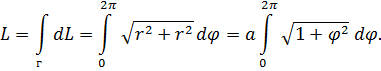
2. Криволинейные интегралы второго рода (криволинейные интегралы по координатам)
П
Рисунок 34
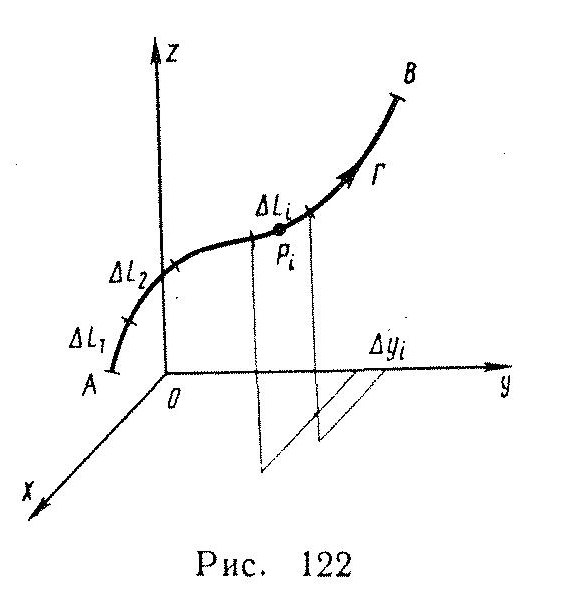 усть в пространстве (или на плоскости) задана кривая линия Г (рисунок 34). Установим на ней определенное направление движения (на чертеже это направление показано стрелкой), которое происходит от А к В. Кривую с установленным на ней направлением движения назовем ориентированной кривой. Если задать по Г движение в противоположную сторону, то получится уже другая ориентированная кривая. Таким образом, ориентированная кривая состоит из кривой и направления движения по этой кривой.
усть в пространстве (или на плоскости) задана кривая линия Г (рисунок 34). Установим на ней определенное направление движения (на чертеже это направление показано стрелкой), которое происходит от А к В. Кривую с установленным на ней направлением движения назовем ориентированной кривой. Если задать по Г движение в противоположную сторону, то получится уже другая ориентированная кривая. Таким образом, ориентированная кривая состоит из кривой и направления движения по этой кривой. Пусть на кривой Г задана функция точки Р в виде f(Р) = f(х, у, z). Разобьем Г на части
L1,
Приступим к составлению интегральной суммы для нового типа интеграла, еще не встречавшеrося у нас. Возьмем на каждой части
(проекции
Если существует предел (не зависящий от способа составления интегральных сумм)