Файл: Криволинейный интеграл по плоской кривой (криволинейный интеграл 1 рода).doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 02.12.2023
Просмотров: 89
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
(46)
то этот предел называется криволинейным интегралом пo координате у от функции f(P) =f(х, у, z) по ориентированной кривой Г и обозначается так:
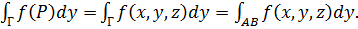 (47)
(47)
Чтобы не спутать этот интеграл с введенным ранее криволинейным интегралом
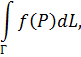
новый интеграл называют криволинейным интегралом второго рода (криволинейным интегралом по координате) в отличие от криволинейного интеграла первого рода (криволинейного интеграла по длине дуги). Точно так же, как был определен интеграл по координате у, определяются и интегралы по координатам х и z:
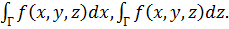 (48)
(48)
Если кривая Г- замкнутая то, чтобы подчеркнуть это обстоятельство, иногда обозначают интеграл по ней так:
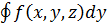 .
.
Первые три основных свойства определенных интегралов сохраняются и здесь:
если кривая разбита на две части Г1 и Г2 и движение по этим частям установлено в том же направлении, как и на всей кривой
4) Предоставляем читателю сообразить, что дает здесь аналог четвертого основного свойства. (для криволинейного интеграла по длине четвертое свойство означало,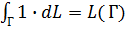 длине - г.)
длине - г.)
5) Если направление движения по кривой Г изменить на противоположное (двигаться от В к A), то знаки всех проекций уi в интегральной сумме (44) сменяются на противоположные и поэтому
уi в интегральной сумме (44) сменяются на противоположные и поэтому
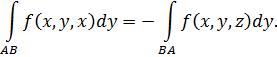
Из ранее рассматривавшийся интегралов аналогичным свойством обладает лишь обычный определенный интеграл
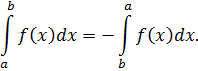
Что же касается криволинейного интеграла по длине, то подчеркнем еще раз - он от направления движения по кривой не зависел (длины
 Li в интегральной сумме (45) всегда положительны)
Li в интегральной сумме (45) всегда положительны)
6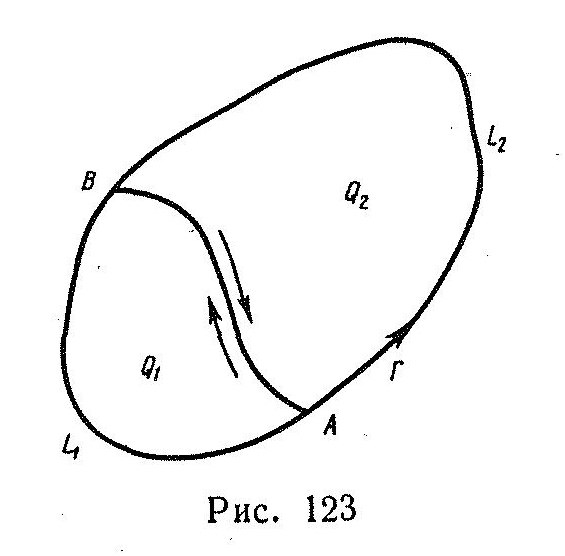
Рисунок 35
) Пусть линия Г замкнута и ограничивает некоторую поверхность Q. Интегрируемая функция f(P) = f(x,у, z) предполагается заданной не только на кривой Г, но и на всей поверхности Q. На кривой Г установим направление обхода, например, такое, чтобы поверхность Q оставалась при движении вдоль Г с левой руки (рисунок 35). Разобьем линией АВ поверхность Q на части Q1 и Q2 с границами L1 и L2, причем движение вдоль L1 и L2 установим так, чтобы Q1 и Q2 соответственно оставались с левой руки. Тогда криволинейный интеграл по замкнутой кривой Г, ограничивающей поверхность Q, равен сумме интегралов по замкнутым кривым L1 и L2, ограничивающим части Q1 и Q2, на которые разбита поверхность:
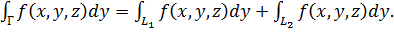 (49)
(49)
Для краткости будем писать только знак интеграла, опуская подынтегральное выражение. Если Г1 - та часть Г, входит в состав границы Q1, a Г2 - та часть Г, что вошла в состав границы Q2, то
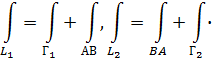
Складывая интегралы по L1 и L2 и применяя свойство, найдем:
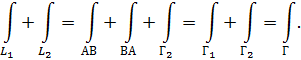
Свойство сохраняется и тогда, когда поверхность делится не на две, а на любое число частей. Это свойство дополняет свойство (3).
Наиболее частым является следующее положение. На кривой Г задаются сразу три функции: Х(х, у, z), Y(х, у, z), Z(х,y, z) (обозначаем их буквами X, Y, Z потому, что эти функции часто полезно понимать в качестве проекций переменного вектора (х, у,z). Выражение
(х, у,z). Выражение
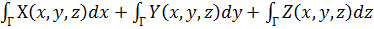 ,
,
можно записать короче, с одним знаком интеграла:
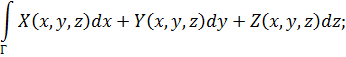
оно называется составным криволинейным интегралом.
П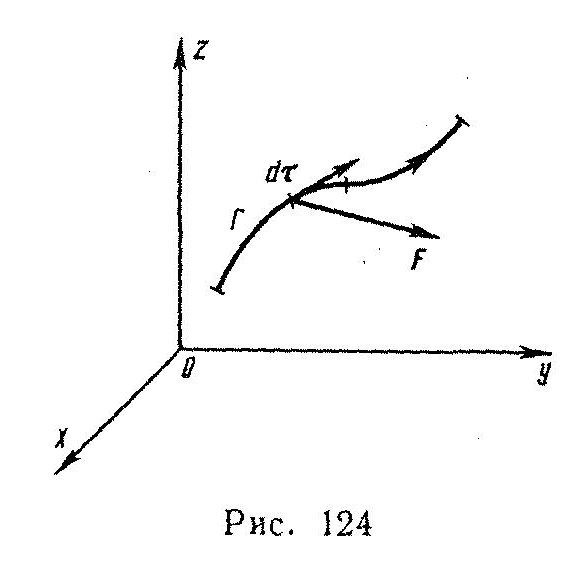
Рисунок 36
усть переменная сила F с проекциями X, Y, Z, являющимися функциями точки (x,y,z ) ее приложения, передвигает материальную точку вдоль кривой Г. Найдем работу этой силы. Выделим бесконечно малый элемент dL кривой Г и заменим его отрезком d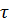 , идущим по касательной (в сторону движения по Г) и имеющим длину dL (рисунок 36). Как известно из дифференциального исчисления проекциями d
, идущим по касательной (в сторону движения по Г) и имеющим длину dL (рисунок 36). Как известно из дифференциального исчисления проекциями d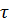 будут дифференциалы dх, dy и dz соответствующих координат. Работа dA силы F (X,Y,Z) на бесконечно малом перемещении d
будут дифференциалы dх, dy и dz соответствующих координат. Работа dA силы F (X,Y,Z) на бесконечно малом перемещении d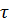 (dх, dy, dz) равна скалярному произведению:
(dх, dy, dz) равна скалярному произведению:
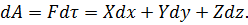
Суммируя все такие элементарные работы, получим полную работу
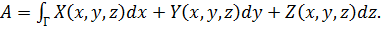 (50)
(50)
Таким образом, составной криволинейный интеграл дает работу силы с проекциями Х, Y, Z вдоль пути Г. Выражение работы в виде составного криволинейного интеграла часто более удобно, чем полученная ранее формула (25) содержащая криволинейный интеграл по длине дуги.
Вычисление криволинейного интеграла по координате сводится к вычислению обычного определенного интеграла.
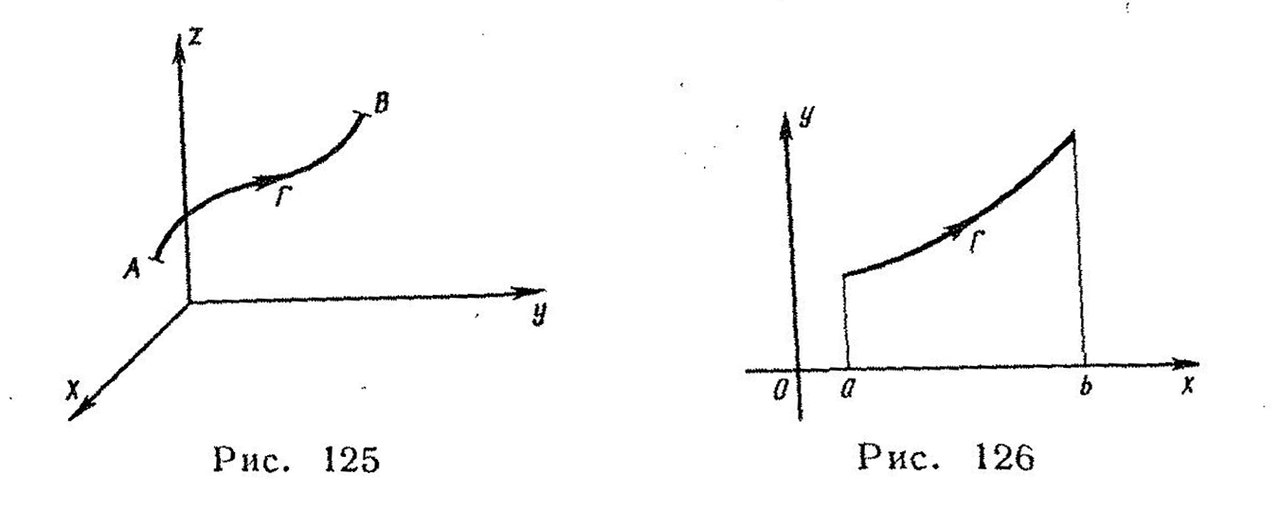
Рисунок 37
Рисунок 38
Пусть кривая Г (рисунок 37) задана параметрическими уравнениями
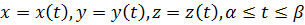 .
.
Если установленное по кривой Г движение от А к В соответствует изменению t от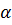 до
до 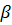 , то
, то
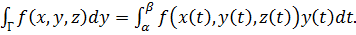 (51)
(51)
Если же движение от А к В соответствует изменению t от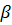
до а, то
а, то
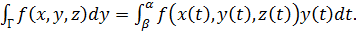 (52)
(52)
Если кривая Г плоская, у=у(х), a a ≤ х ≤b с направлением движения, показанным на рисунке 38, то
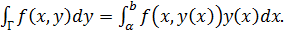 (53)
(53)
Если плоская кривая Г (рисунок 39) задана уравнением х = х(у)
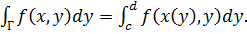 (54)
(54)
Совершенно аналогично вычисляются интегралы и по другим координатам, а также составные.
Если кривая Г распадается на части, заданные различными уравнениями, то надо отдельно вычислить интегралы по этим частям и полученные результаты сложить.
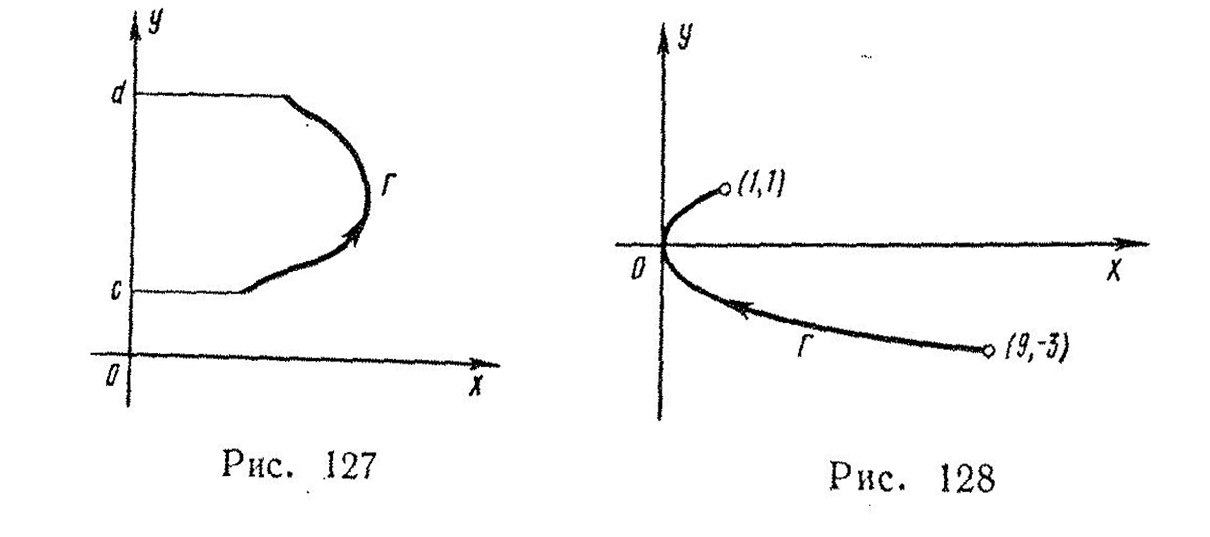
Рисунок 39
Рисунок 40
Таким образом, чтобы вычислить криволинейный интеграл, надо все координаты х, у, z и их дифференциалы dx, dy, dz выразить через переменное, принятое за основное в задании кривой и его дифференциал (в выражении (51) основное переменное t, в (53) - х, в (54) - у). Получившийся обыкновенный определенный интеграл берется в направлении изменения основного переменного, соответствующем обходу контура интегрирования.
Примеры 1. Сила F, зависящая от точки (х, у, z) приложения, имеет проекции X = - y, Y = x, Z = z2. Найти работу силы вдоль первого витка винтовой линии Г.
Имеем: x = acost, y = asint, z = bt, 0 ≤ t ≤ 2 ;
;
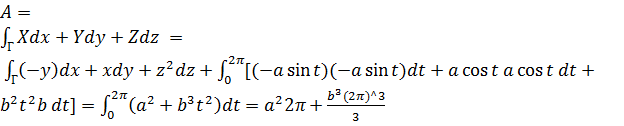 .
.
2. Вычислить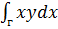 по параболе х = y2 от точки (9,-3) до точки (1,1) (рисунок 40)
по параболе х = y2 от точки (9,-3) до точки (1,1) (рисунок 40)
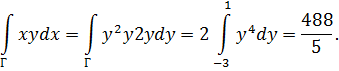
Пусть на кривой Г установлено направление движения. Взяв точку Р на этой кривой, проведем в ней касательную к Г и установим на касательной направление, соответствующее направлению движения по кривой. Отложим по касательной в установленном направлении дифференциал длины дуги dL получим вектор d
(рис. 129), проекциями которого служит дифференциалы dx, dy, dz координат х, у, и z соответственно. Обозначим углы, составляемые касательным вектором d с осями координат х, у и z через
с осями координат х, у и z через  (P),
(P),  (P),
(P), 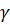 (P) соответственно. Эти углы есть функции от точки Р. Известная формула, дающая проекцию вектора на ось, приводит теперь к соотношениям
(P) соответственно. Эти углы есть функции от точки Р. Известная формула, дающая проекцию вектора на ось, приводит теперь к соотношениям
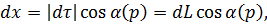

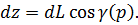 (55)
(55)
Поэтому, например, составной криволинейный интеграл
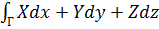 ,
,
может быть заменен интегралом по длине дуги:
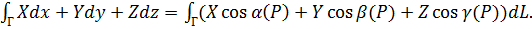 (56)
(56)
Пусть D - плоская область, ограниченная линией Г. В замкнутой области - D (т.е. в области D с включенной границей Г) заданы функции X(x,y) и Y(х, у). Предположим, что эти функции имеют в D частные производные, причем как сами функции так и их частные производные непрерывны в D. На Г зададим направление движения так, чтобы при этом движении область D оставалась с левой руки (обход Г против часовой стрелки). Имеет место следующая формула
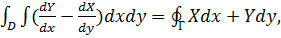
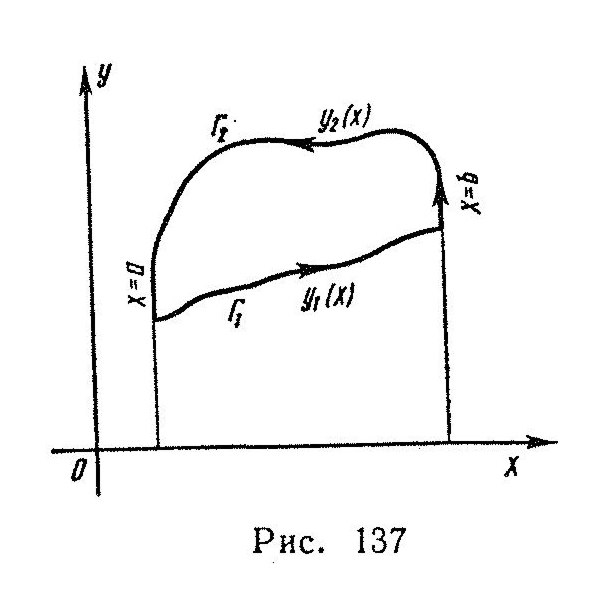 (57)
(57)
которая называется формулой Грина.
Ф
Рисунок 42
ормула Грина и другие формулы, похожие на нее, которые мы рассмотрим в дальнейшем, имеют весьма большое значение. Они позволяют заменять анализ одного явления, происходящего в области (двойной интеграл) анализом другого явления, происходящего только на границе области (криволинейный интеграл). Выведем формулу (57). Эта формула получается сложением двух формул
то этот предел называется криволинейным интегралом пo координате у от функции f(P) =f(х, у, z) по ориентированной кривой Г и обозначается так:
Чтобы не спутать этот интеграл с введенным ранее криволинейным интегралом
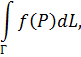
новый интеграл называют криволинейным интегралом второго рода (криволинейным интегралом по координате) в отличие от криволинейного интеграла первого рода (криволинейного интеграла по длине дуги). Точно так же, как был определен интеграл по координате у, определяются и интегралы по координатам х и z:
Если кривая Г- замкнутая то, чтобы подчеркнуть это обстоятельство, иногда обозначают интеграл по ней так:
Первые три основных свойства определенных интегралов сохраняются и здесь:
если кривая разбита на две части Г1 и Г2 и движение по этим частям установлено в том же направлении, как и на всей кривой
4) Предоставляем читателю сообразить, что дает здесь аналог четвертого основного свойства. (для криволинейного интеграла по длине четвертое свойство означало,
5) Если направление движения по кривой Г изменить на противоположное (двигаться от В к A), то знаки всех проекций
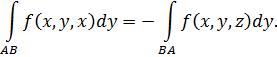
Из ранее рассматривавшийся интегралов аналогичным свойством обладает лишь обычный определенный интеграл
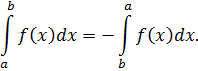
Что же касается криволинейного интеграла по длине, то подчеркнем еще раз - он от направления движения по кривой не зависел (длины
6

Рисунок 35
) Пусть линия Г замкнута и ограничивает некоторую поверхность Q. Интегрируемая функция f(P) = f(x,у, z) предполагается заданной не только на кривой Г, но и на всей поверхности Q. На кривой Г установим направление обхода, например, такое, чтобы поверхность Q оставалась при движении вдоль Г с левой руки (рисунок 35). Разобьем линией АВ поверхность Q на части Q1 и Q2 с границами L1 и L2, причем движение вдоль L1 и L2 установим так, чтобы Q1 и Q2 соответственно оставались с левой руки. Тогда криволинейный интеграл по замкнутой кривой Г, ограничивающей поверхность Q, равен сумме интегралов по замкнутым кривым L1 и L2, ограничивающим части Q1 и Q2, на которые разбита поверхность:
Для краткости будем писать только знак интеграла, опуская подынтегральное выражение. Если Г1 - та часть Г, входит в состав границы Q1, a Г2 - та часть Г, что вошла в состав границы Q2, то
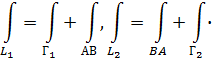
Складывая интегралы по L1 и L2 и применяя свойство, найдем:
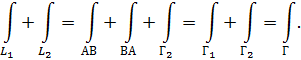
Свойство сохраняется и тогда, когда поверхность делится не на две, а на любое число частей. Это свойство дополняет свойство (3).
3. Составной криволинейный интеграл
Наиболее частым является следующее положение. На кривой Г задаются сразу три функции: Х(х, у, z), Y(х, у, z), Z(х,y, z) (обозначаем их буквами X, Y, Z потому, что эти функции часто полезно понимать в качестве проекций переменного вектора
можно записать короче, с одним знаком интеграла:
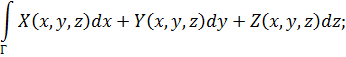
оно называется составным криволинейным интегралом.
П

Рисунок 36
усть переменная сила F с проекциями X, Y, Z, являющимися функциями точки (x,y,z ) ее приложения, передвигает материальную точку вдоль кривой Г. Найдем работу этой силы. Выделим бесконечно малый элемент dL кривой Г и заменим его отрезком d
Суммируя все такие элементарные работы, получим полную работу
Таким образом, составной криволинейный интеграл дает работу силы с проекциями Х, Y, Z вдоль пути Г. Выражение работы в виде составного криволинейного интеграла часто более удобно, чем полученная ранее формула (25) содержащая криволинейный интеграл по длине дуги.
3.1 Вычисление криволинейных интегралов по координатам
Вычисление криволинейного интеграла по координате сводится к вычислению обычного определенного интеграла.

Рисунок 37
Рисунок 38
Пусть кривая Г (рисунок 37) задана параметрическими уравнениями
Если установленное по кривой Г движение от А к В соответствует изменению t от
Если же движение от А к В соответствует изменению t от
до
Если кривая Г плоская, у=у(х), a a ≤ х ≤b с направлением движения, показанным на рисунке 38, то
Если плоская кривая Г (рисунок 39) задана уравнением х = х(у)
Совершенно аналогично вычисляются интегралы и по другим координатам, а также составные.
Если кривая Г распадается на части, заданные различными уравнениями, то надо отдельно вычислить интегралы по этим частям и полученные результаты сложить.

Рисунок 39
Рисунок 40
Таким образом, чтобы вычислить криволинейный интеграл, надо все координаты х, у, z и их дифференциалы dx, dy, dz выразить через переменное, принятое за основное в задании кривой и его дифференциал (в выражении (51) основное переменное t, в (53) - х, в (54) - у). Получившийся обыкновенный определенный интеграл берется в направлении изменения основного переменного, соответствующем обходу контура интегрирования.
Примеры 1. Сила F, зависящая от точки (х, у, z) приложения, имеет проекции X = - y, Y = x, Z = z2. Найти работу силы вдоль первого витка винтовой линии Г.
Имеем: x = acost, y = asint, z = bt, 0 ≤ t ≤ 2
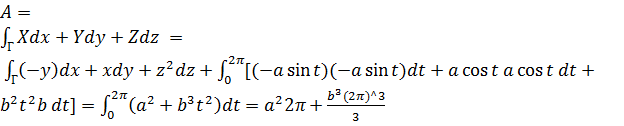 .
.2. Вычислить
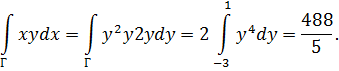
4. Связь криволинейных интегралов первого и второго рода
Пусть на кривой Г установлено направление движения. Взяв точку Р на этой кривой, проведем в ней касательную к Г и установим на касательной направление, соответствующее направлению движения по кривой. Отложим по касательной в установленном направлении дифференциал длины дуги dL получим вектор d
(рис. 129), проекциями которого служит дифференциалы dx, dy, dz координат х, у, и z соответственно. Обозначим углы, составляемые касательным вектором d
Поэтому, например, составной криволинейный интеграл
может быть заменен интегралом по длине дуги:
5. Формула Грина
Пусть D - плоская область, ограниченная линией Г. В замкнутой области - D (т.е. в области D с включенной границей Г) заданы функции X(x,y) и Y(х, у). Предположим, что эти функции имеют в D частные производные, причем как сами функции так и их частные производные непрерывны в D. На Г зададим направление движения так, чтобы при этом движении область D оставалась с левой руки (обход Г против часовой стрелки). Имеет место следующая формула
 (57)
(57)которая называется формулой Грина.
Ф
Рисунок 42
ормула Грина и другие формулы, похожие на нее, которые мы рассмотрим в дальнейшем, имеют весьма большое значение. Они позволяют заменять анализ одного явления, происходящего в области (двойной интеграл) анализом другого явления, происходящего только на границе области (криволинейный интеграл). Выведем формулу (57). Эта формула получается сложением двух формул