Файл: Криволинейный интеграл по плоской кривой (криволинейный интеграл 1 рода).doc

(58)

Для простоты предположим, что граница Г состоит из линий Г₁ и Г₂, заданных уравнениями у = у₁ (х), у = y₂(х), и прямых х = а и х = b (рисунок 42). Вычисляем двойной интеграл:

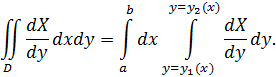
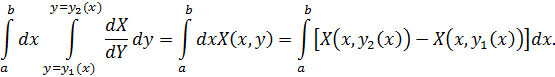
Вычисляем криволинейный интеграл:

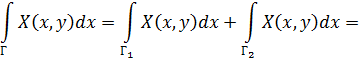
(интегралы по вертикальным прямым х = a и х = b исчезли, так как там dх=0)

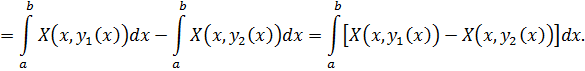
Сравнивая выражения для двойного и криволинейного интегралов, видим, что различие лишь в знаке. Это и приводит к формуле (58).

6. Формула Стокса

Формула Грина является частным случаем более общей формулы Стокса. Пусть в пространстве задана поверхность Q, ограниченная замкнутой кривой Г. Поверхность предполагаем ориентированной, а на контуре Г установим такое направление обхода, чтобы наблюдатель, идущий по Г, направление от ног к голове которого совпадает с направлением n нормали к Q, видел поверхность Q с левой руки (рисунок 43). Пусть на поверхности Q заданы три функции Х(х, у, z), Y(х,у, z), Z(x, y, z), непрерывные вместе с их частными производными. Формула Стокса утверждает, что

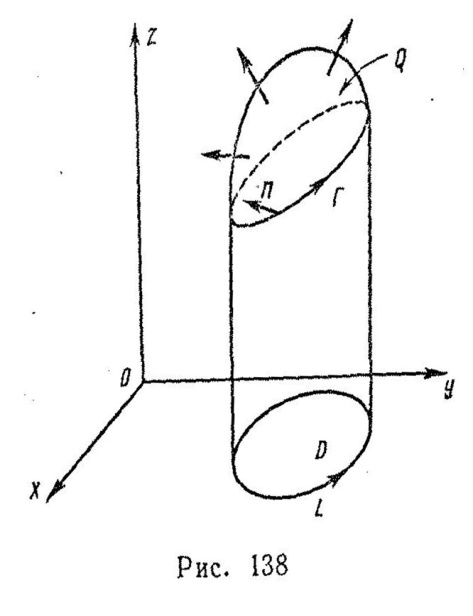
Рисунок 43
тобы запомнить левую часть этой формулы, можно поступить следующим образом. Изобразим переменные х, у и z в виде круговой диаграммы (рисунок 44). Начинаем с х и, продвинувшись до у берем

ф

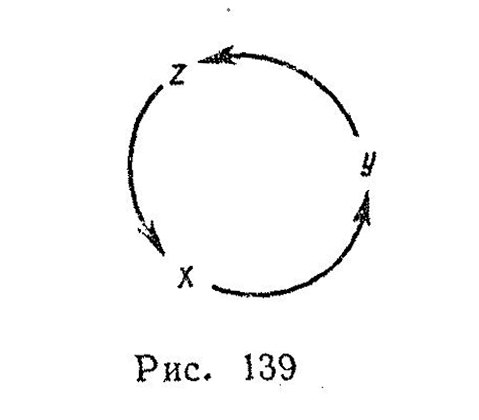ункцию Y, дифференцируем ее по х и вычитаем производную Х по у (занятые в этом члене

Рисунок 44

дифференциалы dхdy от тех же переменных). Теперь начинаем от у (вместо х). Продвинувшись до z , берем функцию Z и дифференцируем ее по у. Раз первый член , то второй будет