Добавлен: 03.12.2023
Просмотров: 100
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Получения числовых характеристик с использованием функции ЛИНЕЙН И ЛГРФПРИБЛ
Результаты расчётов представлены на рис.
| ЛИНЕЙН | |
| 0,0027 | -7,2135 |
| 0,0003 | 0,8217 |
| 0,8257 | 0,0918 |
| 94,7419 | 20 |
| 0,7982 | 0,1685 |
Рисунок 46 - Фрагмент рабочего листа MS Excel использования функции ЛИНЕЙН
для линейной аппроксимации
| ЛИНЕЙН | | |
| 0,0000 | -0,059 | 84,216 |
| 0,0000 | 0,029 | 43,211 |
| 0,8589 | 0,085 | #Н/Д |
| 57,849 | 19 | #Н/Д |
| 0,830 | 0,136 | #Н/Д |
Рисунок 47 - Фрагмент рабочего листа MS Excel использования функции ЛИНЕЙН
Для квадратичной аппроксимации
| ЛГРФПРИБЛ | |
| 1,00390 | 0,00001 |
| 0,00040 | 1,19401 |
| 0,8266 | 0,133386554 |
| 95,37291 | 20 |
| 1,69687 | 0,35584 |
Рисунок 48 -. Фрагмент рабочего стола MS Excel использование функции ЛГРФПРИБЛ
для экспоненциальной аппроксимации
Сравнивая результаты, полученные с помощью функции ЛИНЕЙН и ЛГРФПРИБЛ, с результатами полученными вручную с использованием основных расчётов формул, можно видеть , что они полностью совпадают. Это указывает на то, что вычисления верны.
Лучше всего результаты испытаний, аппроксимирует квадратичная функция: y = 1E-05x2 - 0,059x + 84,216 т.к коэффициент детерминировнности квадратичной аппроксимации выше и равен R2 = 0,859. Значения числовых характеристик вычислялись разными способами и все результаты совпали, что свидетельствует об их правильности.
-
Аппроксимация с помощью MathCAD
Вводим исходные данные(рис.49)
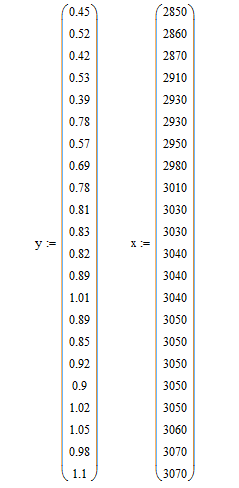
Рисунок 49 - Фрагмент листа MathCAD с исходными данными
Линейная регрессия
Линейная регрессия в системе MathCAD выполняется по векторам аргумента Х и отсчетов Y функциями: intercept(X,Y) – вычисляет параметр a1 , смещение линии регрессии по вертикали; slope(X,Y) – вычисляет параметр a2 , угловой коэффициент линии регрессии. Полученные значения коэффициентов используем в уравнении регрессии
Функция corr(Y,y(x)) - вычисляет коэффициент корреляции Пирсона. Чем он ближе к 1, тем точнее обрабатываемые данные соответствуют линейной зависимости.
Вычислив параметры линейной регрессии, строим графики исходной функции y и функции линейной регрессии f(x)
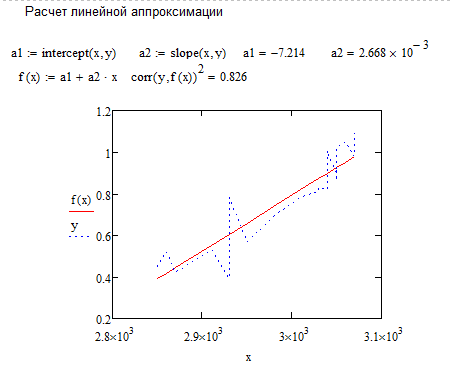
Рисунок 50 - Фрагмент листа MathCAD с найденными коэффициентами для системы уравнений и графиком зависимости линии тренда для линейной аппроксимации
Полиномиальная регрессия
Одномерная полиномиальная регрессия с произвольной степенью n полинома и с произвольными координатами отсчетов в MathCAD выполняется функцией regress(X,Y,n), которая вычисляет вектор S, в составе которого находятся коэффициенты ai полинома n-й степени. Значения коэффициентов ai могут быть извлечены из вектора S функцией submatrix(S, 3, length(S)-1, 0, 0). Полученные значения коэффициентов используем в уравнении регрессии/ Вычислив параметры квадратичной регрессии, строим графики исходной функции y и функции квадратичной регрессии f(x)
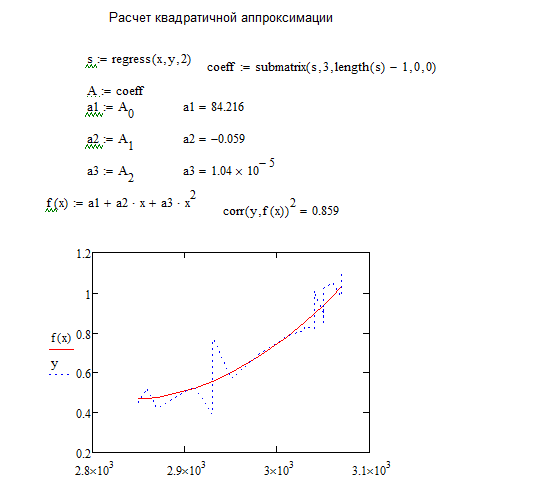
Рисунок 51 - Фрагмент листа MathCAD с найденными коэффициентами для системы уравнений и графиком зависимости линии тренда для квадратичной аппроксимации
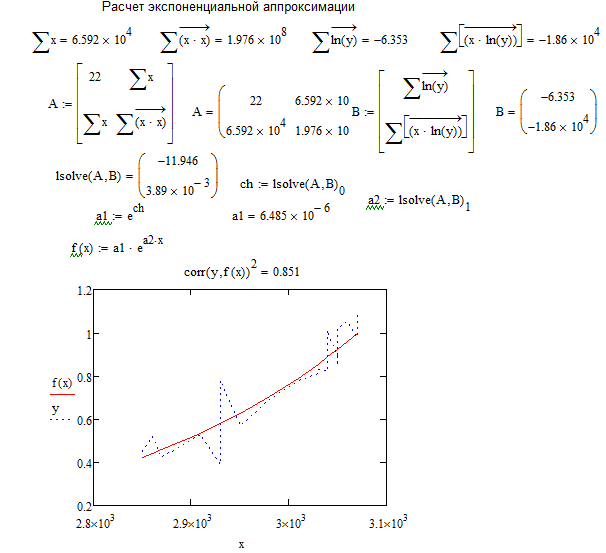
Рисунок 52 - Фрагмент листа MathCAD с найденными коэффициентами для системы уравнений и графиком зависимости линии тренда для экспоненциальной аппроксимации
Проведенные расчеты показывают, что результаты, полученные с помощью среды MathCAD, полностью совпадают со значениями, рассчитанными в MS Excel.
-
Аппроксимация с помощью VBA
Код программы:
Public Sub MHK()
Dim x(1 To 22) As Single, y(1 To 22) As Single, yt(1 To 22), yt1(1 To 22), yt2(1 To 22) As Single
Dim Sx1, Sx2, Sx3, Sx4 As Single
Dim Sy, Sxy, Sx2y As Single
Dim x1, x2, x3, x4 As Single
Dim y1, y2, sxr, yxr, lny1, slny, sxlny, sxsrysr As Single
Dim n As Integer
Dim i As Integer
Dim a1 As Single, a2 As Single
Dim coef_cor As Single
Dim coef_det As Single
Dim coef_det2 As Single
Dim coef_det3 As Single
n = 22
' ââîäèì èñõîäíûå äàííûå â âåêòîðà x è y
For i = 1 To n
x(i) = Range("B" & 2 + i)
y(i) = Range("a" & 2 + i)
xsr = xsr + x(i)
ysr = xsr + y(i)
Next i
xsr = xsr / 22
ysr = ysr / 22
' îïðåäåëÿåì êîýô ÑËÀÓ
Sx1 = 0
Sx2 = 0
Sx3 = 0
Sx4 = 0
Sy1 = 0
Sxy = 0
Sx2y = 0
For i = 1 To n
x1 = x(i)
y1 = y(i)
lny1 = Log(y1)
x2 = x1 * x1
x3 = x2 * x1
x4 = x3 * x1
Sx1 = Sx1 + x1
Sx2 = Sx2 + x2
Sx3 = Sx3 + x3
Sx4 = Sx4 + x4
Sy1 = Sy1 + y1
Sxy = Sxy + x1 * y1
Sx2y = Sx2y + x2 * y1
slny = slny + lny1
sxlny = sxlny + x1 * lny1
sxsrysr = sxsrysr + ((x1 - xsr) * (y1 - ysr))
Next i
'ðåøàåì ÑËÀÓ ìåòîäîì Êðàìåðà
Call kram2(22, Sx1, Sx1, Sx2, Sy1, Sxy, a1, a2)
MsgBox "Ëèíåéíàÿ àïïðîêñèìàöèÿ"
MsgBox "a1= " & a1
MsgBox "a2= " & a2
'âû÷èñëÿåì ñðåäíåå çíà÷åíèå äëÿ x è y
xsr = Sx1 / n
ysr = Sy1 / n
'âû÷èñëÿåì êîýôôèöèåíò êîððåëÿöèè
Sxy_mean = 0
Sx2_mean = 0
Sy2_mean = 0
For i = 1 To n
Sxy_mean = Sxy_mean + (x(i) - xsr) * (y(i) - ysr)
Sx2_mean = Sx2_mean + (x(i) - xsr) ^ 2
Sy2_mean = Sy2_mean + (y(i) - ysr) ^ 2
Next i
coef_cor = Sxy_mean / Sqr(Sx2_mean) / Sqr(Sy2_mean)
MsgBox "êîýôôèöèåíò êîððåëÿöèè =" & coef_cor
'âû÷èñëÿåì âåêòîð òåîðåòè÷åñêèõ çíà÷åíèé yt
For i = 1 To n
yt(i) = line(x(i), a1, a2)
Next i
Call kram3(22, Sx1, Sx2, Sx1, Sx2, Sx3, Sx2, Sx3, Sx4, Sy1, Sxy, Sx2y, a1, a2, a3)
MsgBox "Êâàäðàòè÷íàÿ àïïðîêñèìàöèÿ"
MsgBox "a1= " & a1
MsgBox "a2= " & a2
MsgBox "a3= " & a3
For i = 1 To 10
yt1(i) = kvad(x(i), a1, a2, a3)
Next i
Call kram4(22, Sx1, Sx1, Sx2, slny, sxlny, a1, a2)
MsgBox "Ýêñïîíåíöèàëüíàÿ àïïðîêñèìàöèÿ"
MsgBox "a1= " & a1
MsgBox "a2= " & a2
For i = 1 To 10
yt2(i) = expon(x(i), a1, a2)
Next i
End Sub
Public Sub kram2(a11, a12, a21, a22, b1, b2, x1, x2)
Dim d, d1, d2 As Single
d = a11 * a22 - a21 * a12
d1 = b1 * a22 - b2 * a12
d2 = a11 * b2 - a21 * b1
x1 = d1 / d
x2 = d2 / d
End Sub
Public Sub kram3(a11, a12, a13, a21, a22, a23, a31, a32, a33, b1, b2, b3, x1, x2, x3)
Dim d, d1, d2, d3 As Single
d = a11 * a22 * a33 + a12 * a23 * a31 + a13 * a21 * a32 - a13 * a22 * a31 - a12 * a21 * a33 - a11 * a23 * a32
d1 = b1 * a22 * a33 + b2 * a23 * a31 + b3 * a21 * a32 - b3 * a22 * a31 - b2 * a21 * a33 - b1 * a23 * a32
d2 = a11 * b2 * a33 + a12 * b3 * a31 + a13 * b1 * a32 - a13 * b2 * a31 - a12 * b1 * a33 - a11 * b3 * a32
d3 = a11 * a22 * b3 + a12 * a23 * b1 + a13 * a21 * b2 - a13 * a22 * b1 - a12 * a21 * b3 - a11 * a23 * b2
x1 = d1 / d
x2 = d2 / d
x3 = d3 / d
End Sub
Public Sub kram4(a11, a12, a21, a22, b1, b2, x1, x2)
Dim d, d1, d2 As Single
d = a11 * a22 - a21 * a12
d1 = b1 * a22 - b2 * a12
d2 = a11 * b2 - a21 * b1
x1 = exp(d1 / d)
x2 = d2 / d
End Sub
Public Function line(x, b, a) As Single
line = a * x + b
End Function
Public Function kvad(x, b, a1, a2) As Single
kvad = a2 * x * x + a1 * x + b
End Function
Public Function expon(x, a1, a2) As Single
expon = a1 * e ^ (a2 * x)
End Function
Public Function r2(n, ysr, y, yt) As Single
sost = 0
sfact = 0
For i = 1 To 22
sost = sost + (y(i) - yt(i)) ^ 2
sfact = sfact + (yt(i) - ysr) ^ 2
Next i
r2 = 1 - sost / (sost + sfact)
EndFunction
Результат работы программы представлен на рисунках
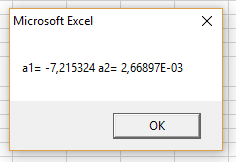
Рисунок 53 – Результат работы программы (Линейная аппроксимация)
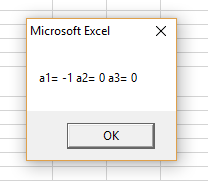
Рисунок 54 – Результат работы программы (Квадратичная аппроксимация)
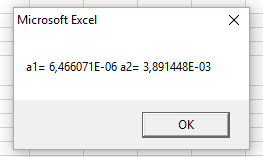
Рисунок 55 – Результат работы программы (Экспоненциальная аппроксимация)
-
Вывод.
Сравнивая результаты расчетов, полученных средствами табличного процессора MS Excel и математического пакета MathCAD, видим, что они практически совпадают. Пренебрежительно малые расхождения обусловлены тем, что MathCAD округляет значения, в то время как MS Excel вычисляет точно.
Вывод по задаче 1:
Лучше всего результаты испытаний, аппроксимирует квадратичная функция (24): y = 0,0021x
2 + 22,672x - 24886 т.к коэффициент детерминировнности квадратичной аппроксимации выше и равен R2 = 0,993. Значения числовых характеристик вычислялись разными способами и все результаты совпали, что свидетельствует об их правильности.
Вывод по задаче 2:
Лучше всего результаты испытаний, аппроксимирует квадратичная функция: y = -0,0006x2 + 0,0668x - 0,6756 т.к коэффициент детерминировнности квадратичной аппроксимации выше и равен R2 = 0,8733. Значения числовых характеристик вычислялись разными способами и все результаты совпали, что свидетельствует об их правильности.
Вывод по задаче 3:
Лучше всего результаты испытаний, аппроксимирует квадратичная функция: y = 1E-05x2 - 0,059x + 84,216 т.к коэффициент детерминировнности квадратичной аппроксимации выше и равен R2 = 0,859. Значения числовых характеристик вычислялись разными способами и все результаты совпали, что свидетельствует об их правильности.
6. Список литературы.
-
Методические указания по выполнению курсовой работы для студентов специальности 130403. /Беляев В.В., Саттарова Н. И. – СПб.: РИЦ горн. ин-т., 2010 -
Правила оформления курсовых и квалификационных работ. Методические указания. /Онушкина И.О., Талалай П. Г. – СПб.: РИЦ горн. ин-т., 2005