Файл: Информационные процессы в переработке нефти и газа.doc

Задача 2

Вариант 6

0,48	20,8
0,39	21,4
0,39	21,5
0,52	21,6
0,45	24,1
0,68	24,8
0,78	28,2
0,84	28,7
0,65	30,5
0,82	30,9
0,76	31,3
0,7	32,7
0,88	33,3
0,86	34,4
0,95	34,9
0,83	36,3
0,84	36,5
0,94	37,4
0,94	38
1,01	38,1
0,88	38,6
0,89	38,9
0,96	41,1
1,08	43,5
0,97	43,8
1,04	44

1. Таблицы, выполненные средствами Microsoft Excel.

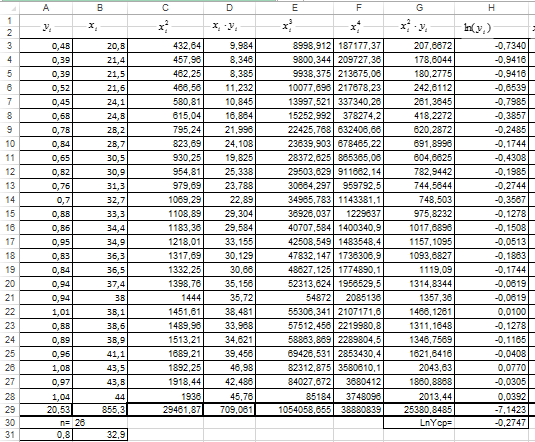
Рисунок 20 вычисления вспомогательных сумм и средних значений.



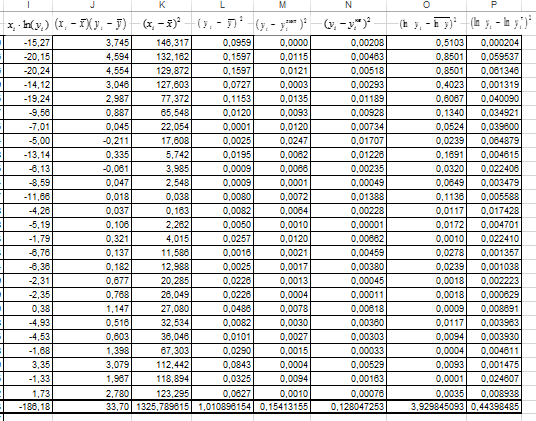
Рисунок 21 - Вычисления вспомогательных сумм (продолжения).
На рис. 22 представлены расчёты для линейной аппроксимации.

26	855,3	20,53	Линейная
855,3	29461,87	709,061	аппроксимация
				0,9206
Обратная матрица				0,84753
0,8547	-0,0248		a1=	-0,0466
-0,0248	0,00075427		a2=	0,0254

---

Рисунок 22 - Фрагмент рабочего листа MS Excel для линейной аппроксимации.

Таким образом уравнение линейной регрессии имеет вид:

y = 0,0254x - 0,0466

На рис. 23 представлены расчёты для квадратичной аппроксимации.

26	855,3	29461,87	20,53	Квадратичная
855,3	29461,87	1054058,655	709,061	аппроксимация
29461,87	1054058,66	38880839,39	25380,849
					0,87333
Обратная матрица
16,0209	-1,0228	0,0156		a1=	-0,676
-1,0228	0,0664	-0,0010		a2=	0,067
0,0156	-0,0010	0,000016		a3=	-0,001

Рисунок 23 Фрагмент рабочего листа MS Excel для квадратичной аппроксимации

Таким образом, уравнение квадратичной регрессии имеет вид:

y = -0,0006x² + 0,0668x - 0,6756

На рис. 24 представлены расчёты для экспоненциальной аппроксимации.

26	855,3	-7,14	Экспоненциальная
855,3	29461,87	-186,18	аппрокимация
				0,8016
Обратная матрица			c=	-1,48483
0,8547	-0,02481		a2=	0,0368
-0,0248	0,00075		a1=	0,2265

---

Рисунок 24 - Фрагмент листа MS Excel для экспоненциальной аппроксимации.

Таким образом, уравнение экспоненциальной регрессии имеет вид:

y = 0,2265e^0,0368x (25)

2. 1   2   3   4   5   6   7   8   9   10

---

Представление результатов в виде графиков

Построение линии тренда

Методика проведения данных работ подробно изложена в работе [2]. Результаты представлены на рис.



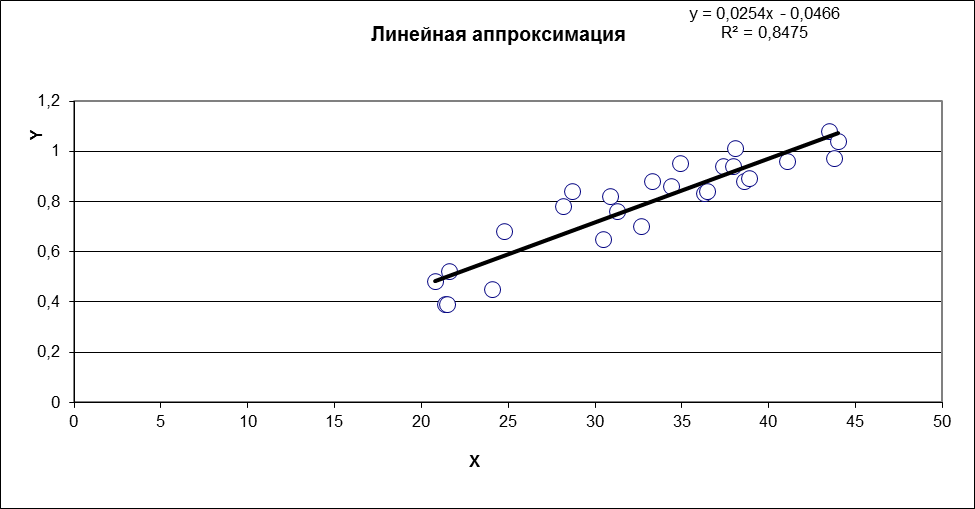
Рисунок 25 - Исходные точки и линия тренда для линейной аппроксимации.



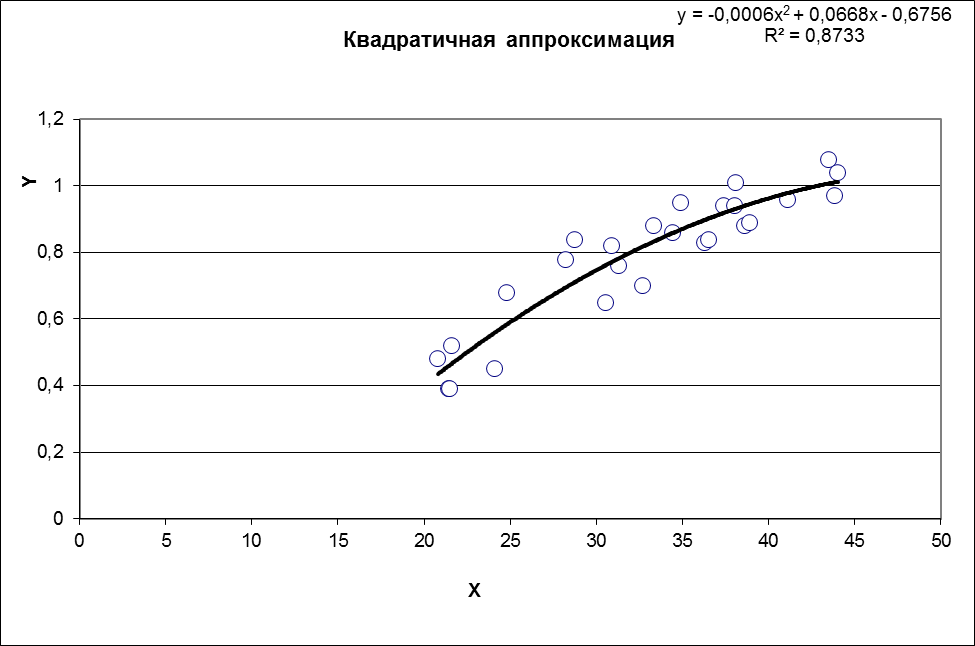
Рисунок 26 -. Исходные точки и линия тренда для квадратичной аппроксимации.



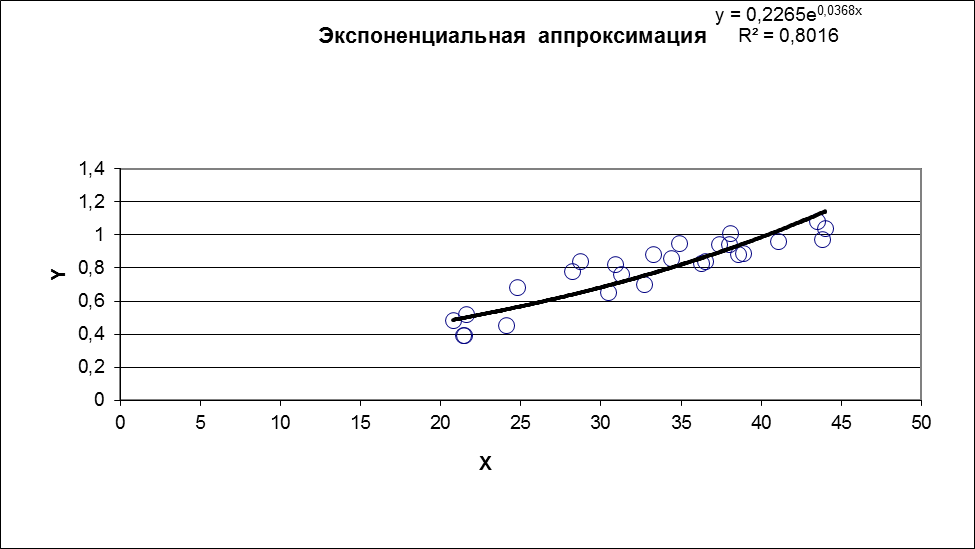
Рисунок 27 - Исходные точки и линия тренда для экспоненциальной аппроксимации.

Сравнивая данные результаты с результатами, полученными вручную ранее с использованием основных расчётных формул, видим, что они полностью совпадают. Это указывает на то, что вычисления верны.

3. Получения числовых характеристик с использованием функции ЛИНЕЙН И ЛГРФПРИБЛ

Результаты расчётов представлены на рис.

ЛИНЕЙН
0,0254	-0,0466
0,0022	0,0741
0,8475	0,0801
133,4078	24
0,8568	0,1541

Рисунок 28 - Фрагмент рабочего листа MS Excel использования функции ЛИНЕЙН

для линейной аппроксимации

ЛИНЕЙН
-0,0006	0,067	-0,676
0,0003	0,019	0,299
0,8733	0,075	#Н/Д
79,289	23	#Н/Д
0,883	0,128	#Н/Д

---

Рисунок 29 - Фрагмент рабочего листа MS Excel использования функции ЛИНЕЙН

Для квадратичной аппроксимации

ЛГРФПРИБЛ
1,03747	0,22654
0,00374	0,12574
0,8016	0,136012385
96,98172	24
1,79410	0,44398

Рисунок 30 -. Фрагмент рабочего стола MS Excel использование функции ЛГРФПРИБЛ

для экспоненциальной аппроксимации

Сравнивая результаты, полученные с помощью функции ЛИНЕЙН и ЛГРФПРИБЛ, с результатами полученными вручную с использованием основных расчётов формул, можно видеть , что они полностью совпадают. Это указывает на то, что вычисления верны.

Лучше всего результаты испытаний, аппроксимирует квадратичная функция: y = -0,0006x² + 0,0668x - 0,6756 т.к коэффициент детерминировнности квадратичной аппроксимации выше и равен R² = 0,8733. Значения числовых характеристик вычислялись разными способами и все результаты совпали, что свидетельствует об их правильности.

4. 1   2   3   4   5   6   7   8   9   10

---