Добавлен: 03.12.2023
Просмотров: 101
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
(8)
Где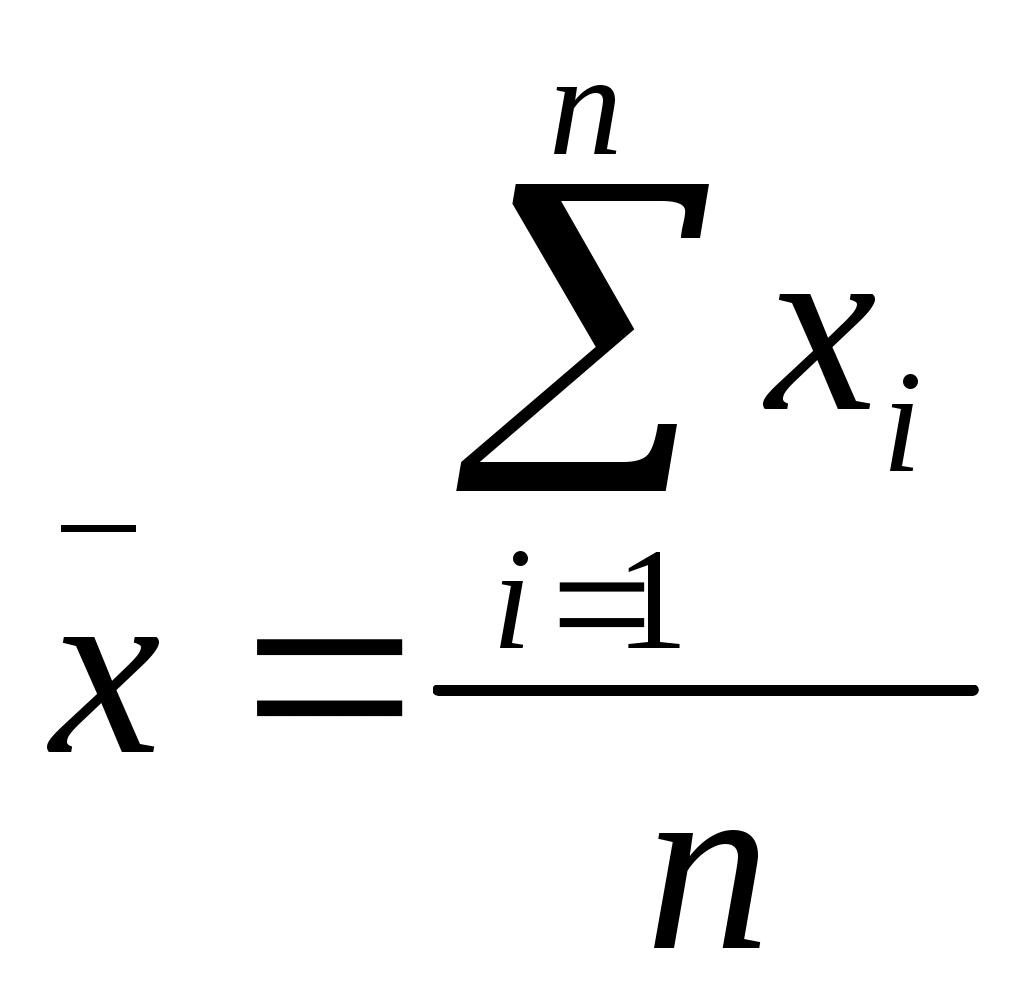 ,
, 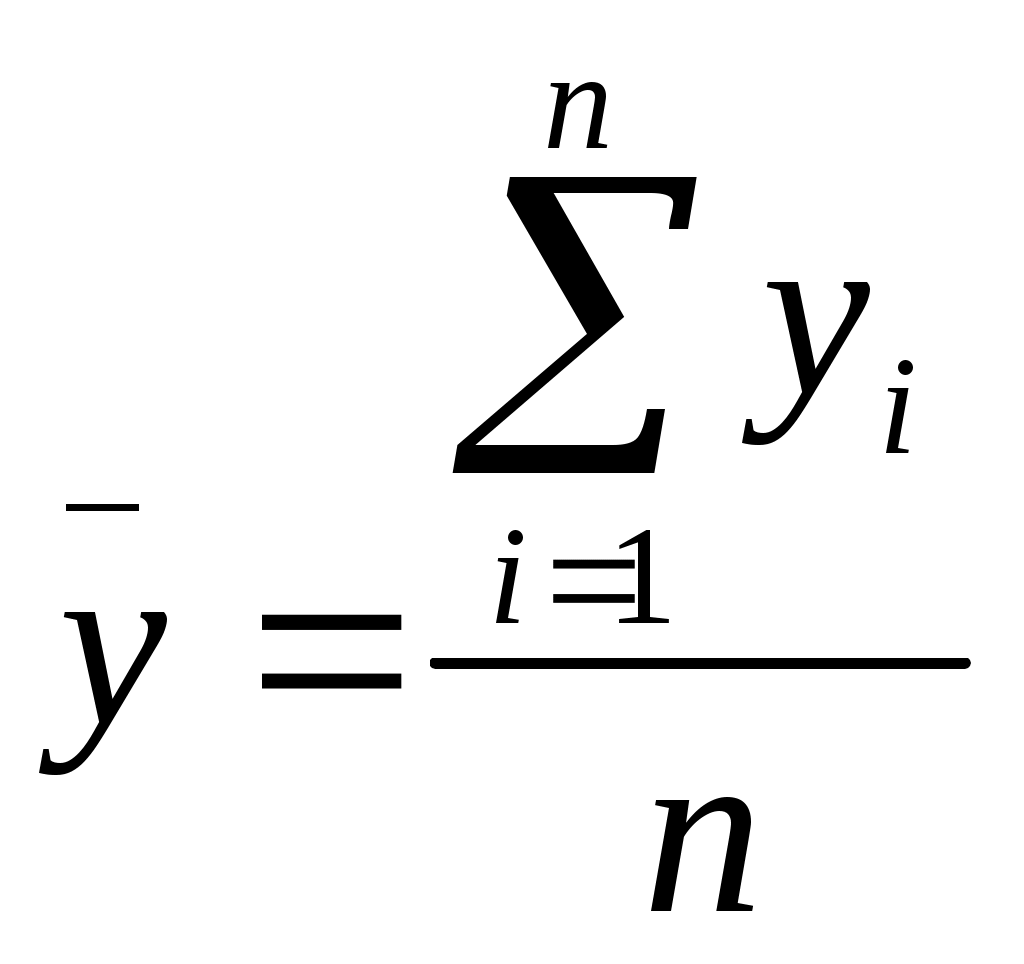 ,
, 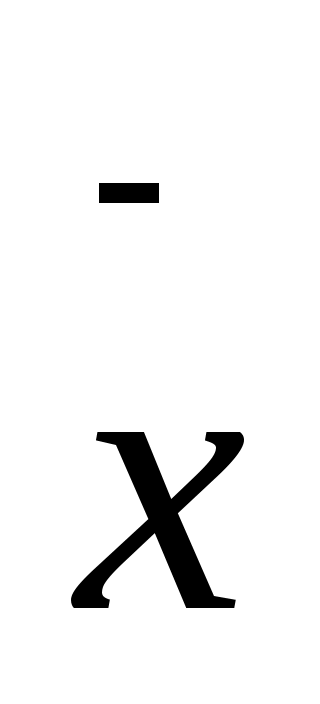 и
и 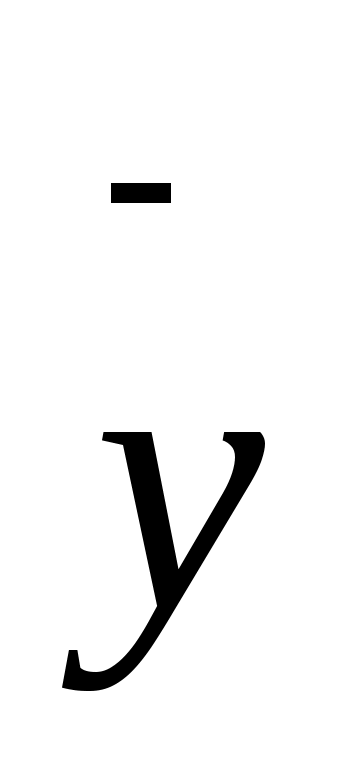 - среднее арифметическое значения соответственно по x и y.
- среднее арифметическое значения соответственно по x и y.
Коэффициент детерминированности ( детерминации) определяться по формуле:
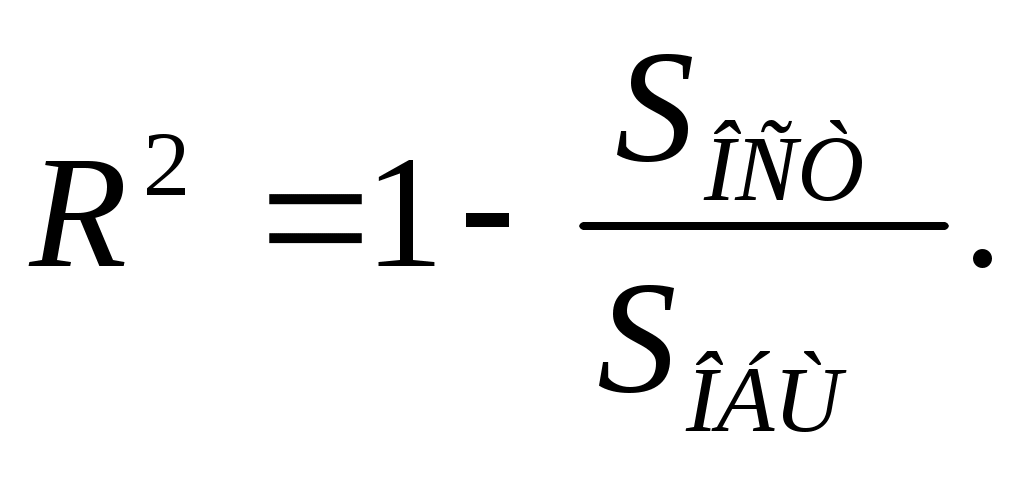 (9)
(9)
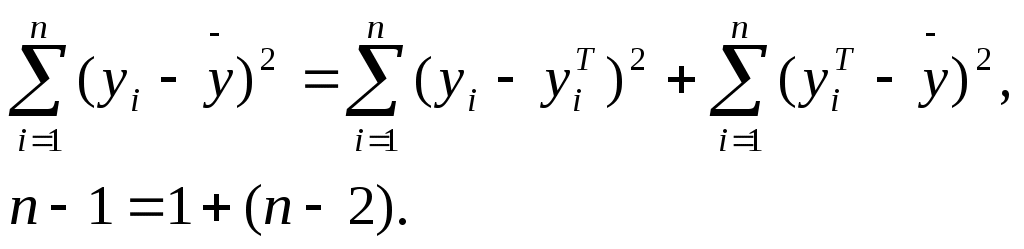 (10)
(10)
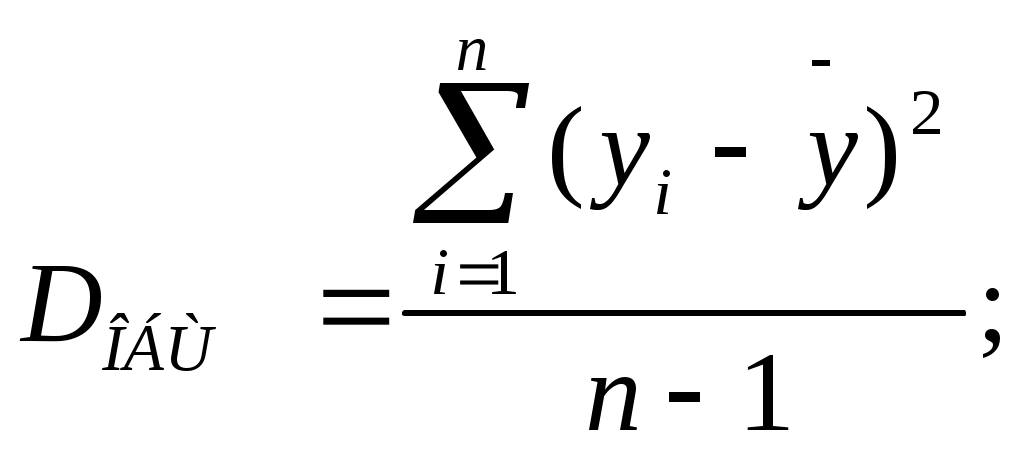 (11)
(11)
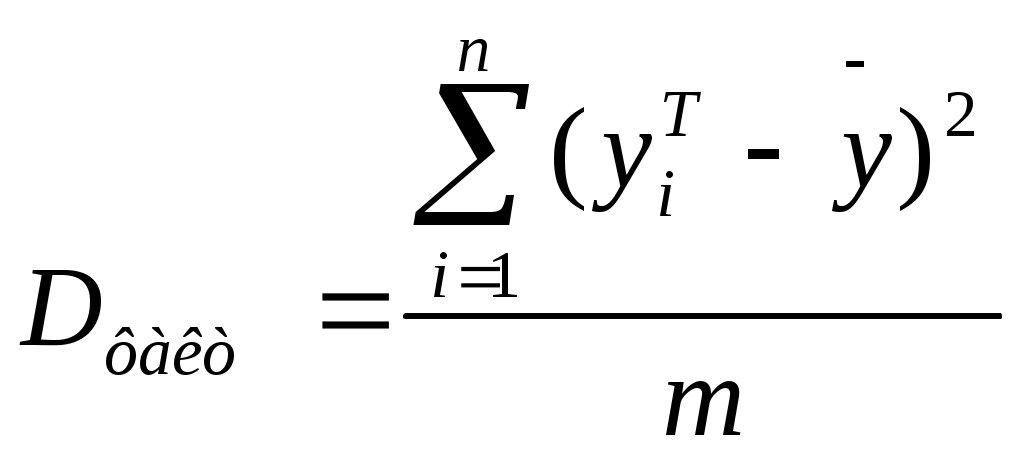 ; (12)
; (12)
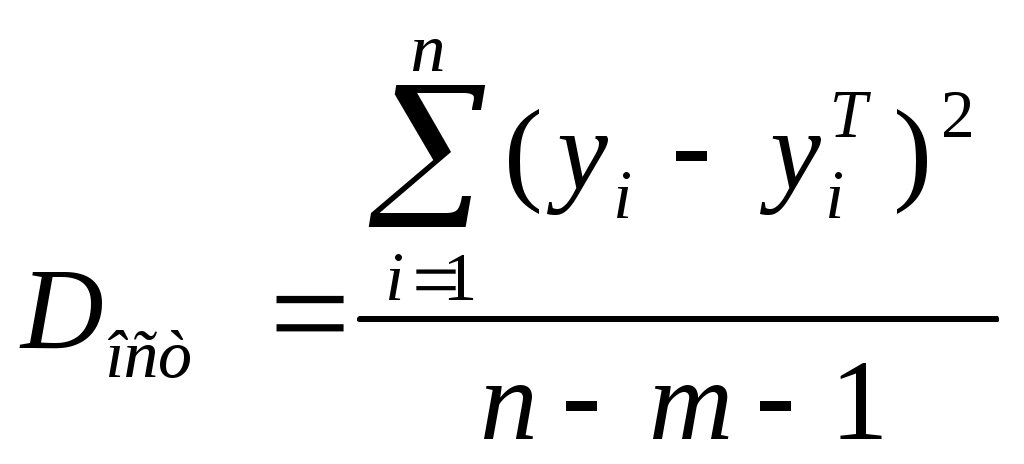 , (13)
, (13)
Где m- число параметров при переменных x.
Для линейной и экспоненциальной аппроксимации m=1, для квадратичной аппроксимации m=2.
Критерий Фишера определяться соотношение:
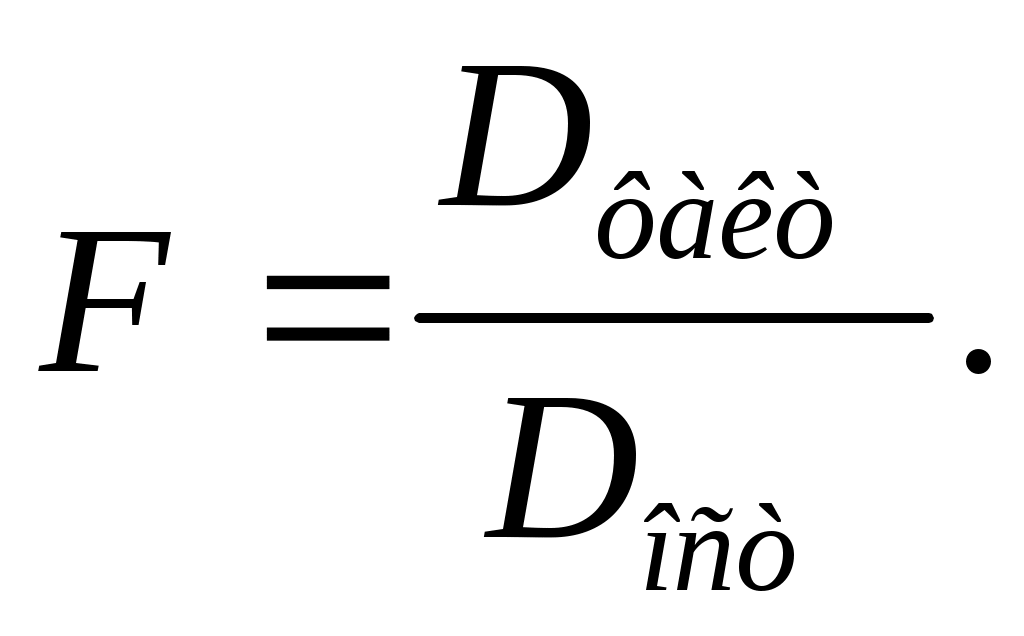 (14)
(14)
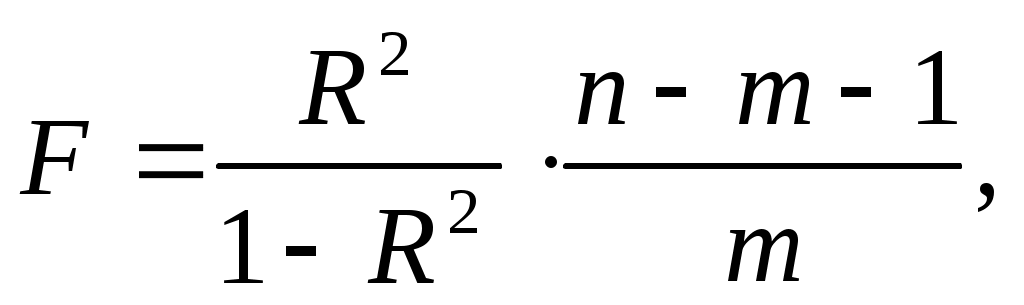 (15)
(15)
Для линейной и экспоненциальной функции формула имеет вид:
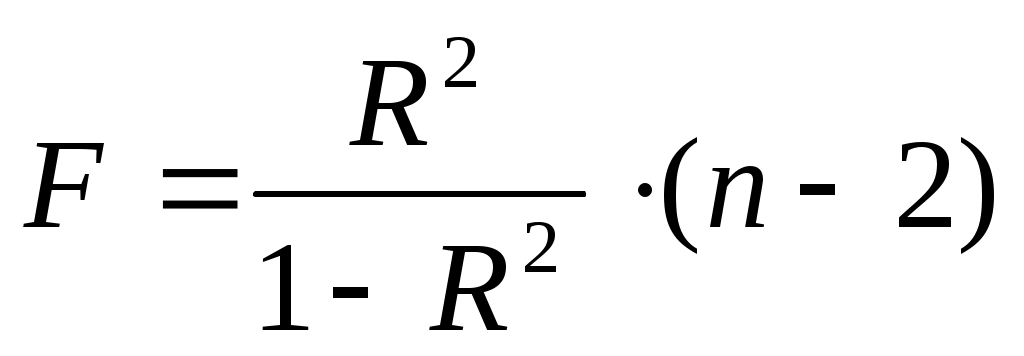 . (16)
. (16)
Для параболы формула F- критерия будет :
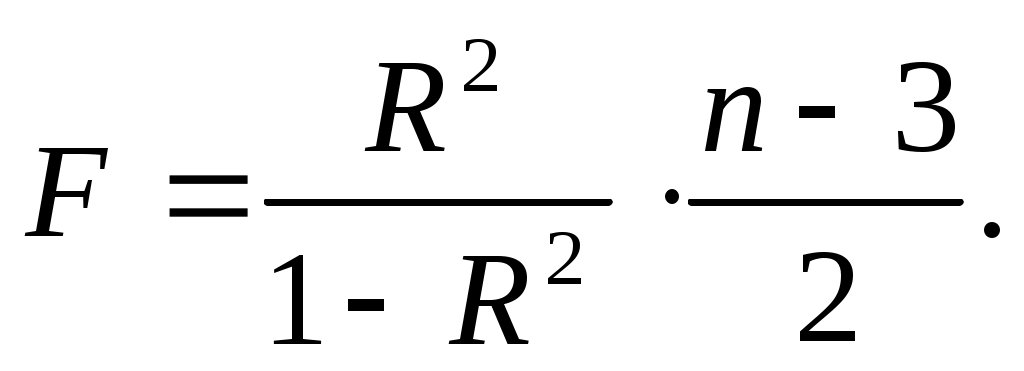 (17)
(17)
Стандартная ошибка коэффициента регрессии определяется по формуле :
определяется по формуле :
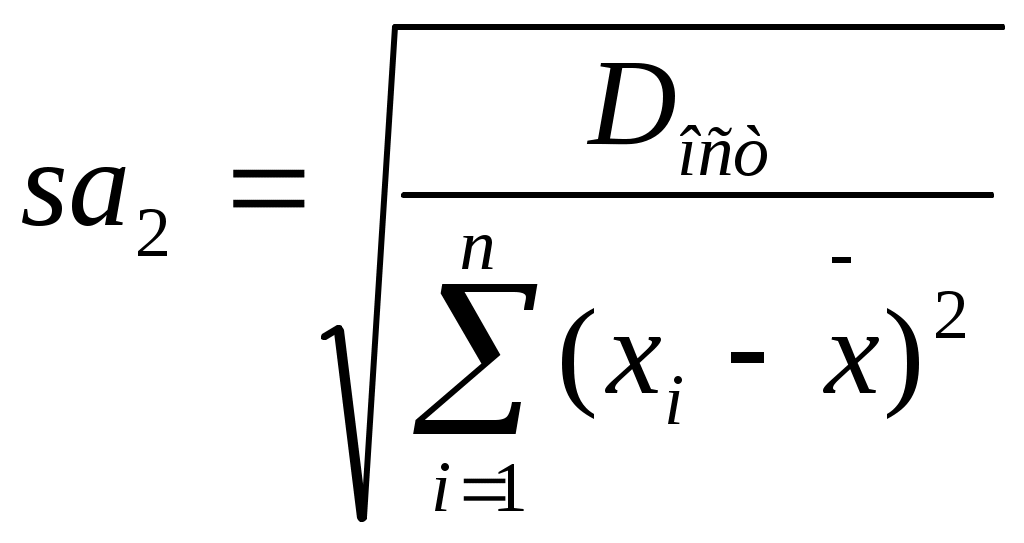 . (18)
. (18)
Стандартная ошибка параметра :
:
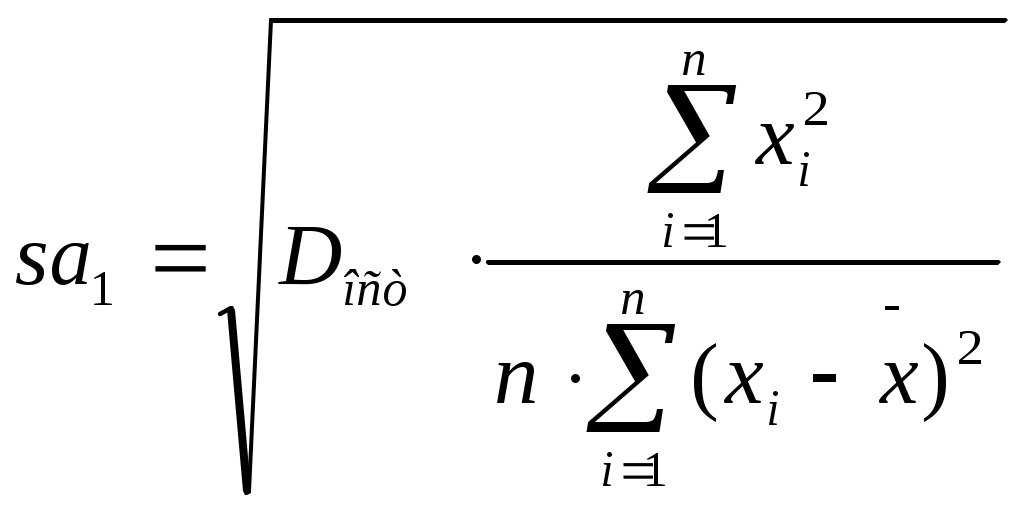 . (19)
. (19)
Для оценки значимости квадратичной зависимости используется аналогичный подход. Значения стандартных ошибок вычисляются по формулам:
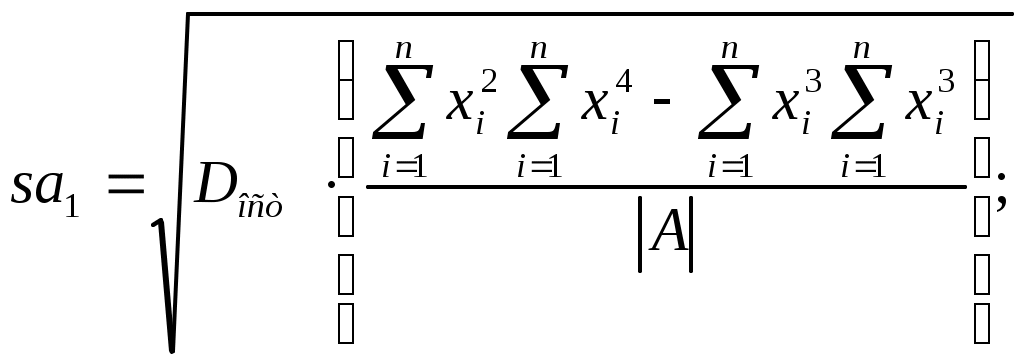 (20)
(20)
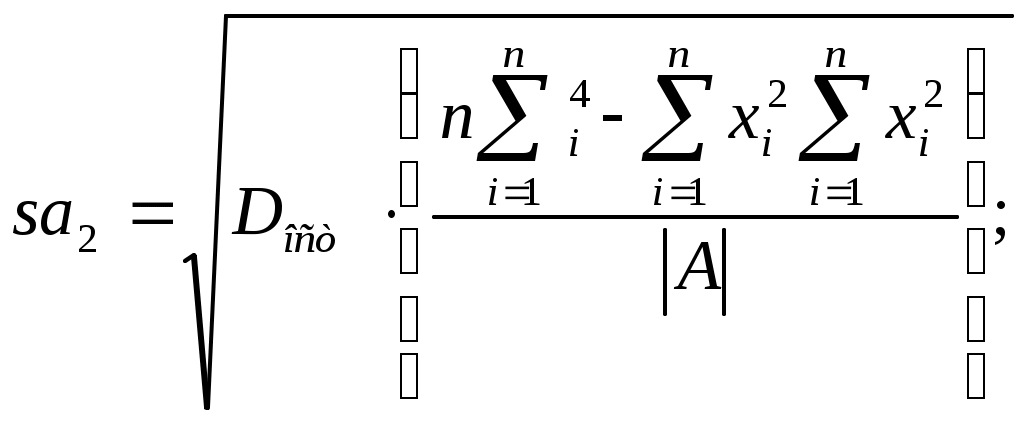 (21)
(21)
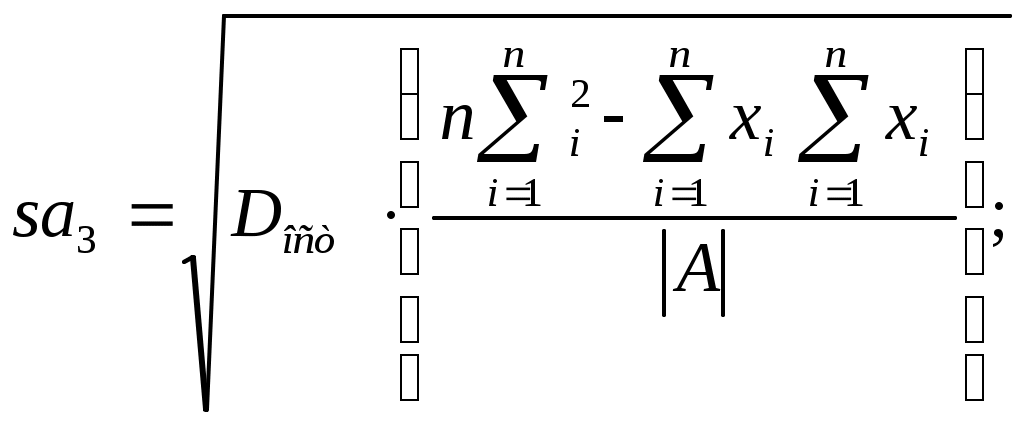
. (22)
Вариант 6
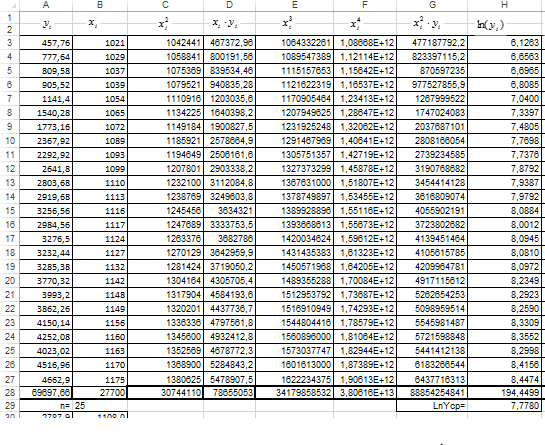
Рисунок 1 вычисления вспомогательных сумм и средних значений.
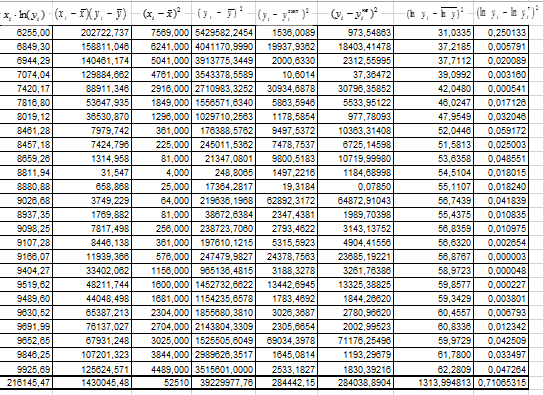
Рисунок 2 - Вычисления вспомогательных сумм (продолжения).
На рис. 3 представлены расчёты для линейной аппроксимации.
Рисунок 3 - Фрагмент рабочего листа MS Excel для линейной аппроксимации.
Таким образом уравнение линейной регрессии имеет вид:
y = 27,234x - 27387 (23)
На рис. 4 представлены расчёты для квадратичной аппроксимации.
Рисунок 4 Фрагмент рабочего листа MS Excel для квадратичной аппроксимации
Таким образом, уравнение квадратичной регрессии имеет вид:
y = 0,0021x2 + 22,672x - 24886 (24)
На рис. 6 представлены расчёты для экспоненциальной аппроксимации.
Рисунок 6 - Фрагмент листа MS Excel для экспоненциальной аппроксимации.
Таким образом, уравнение экспоненциальной регрессии имеет вид:
y = 0,001e0,0132x (25)
Где
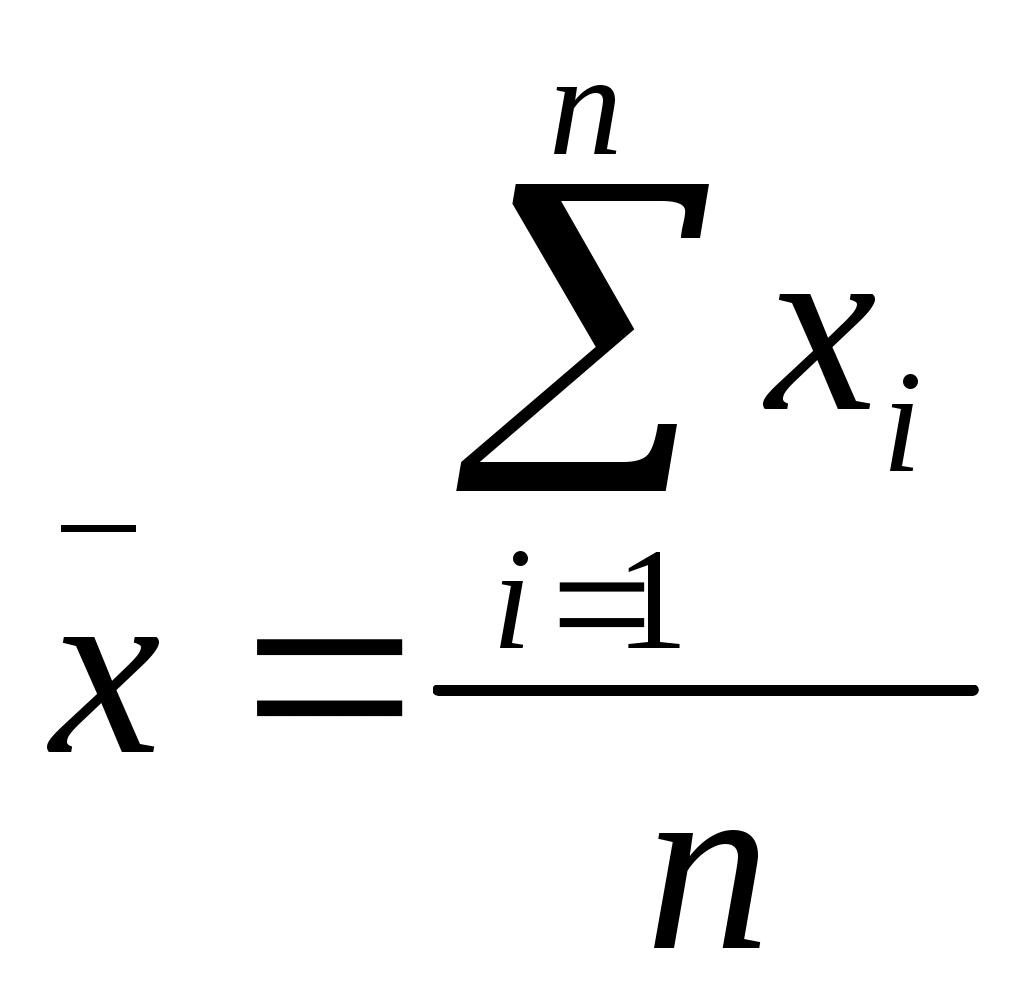 ,
, 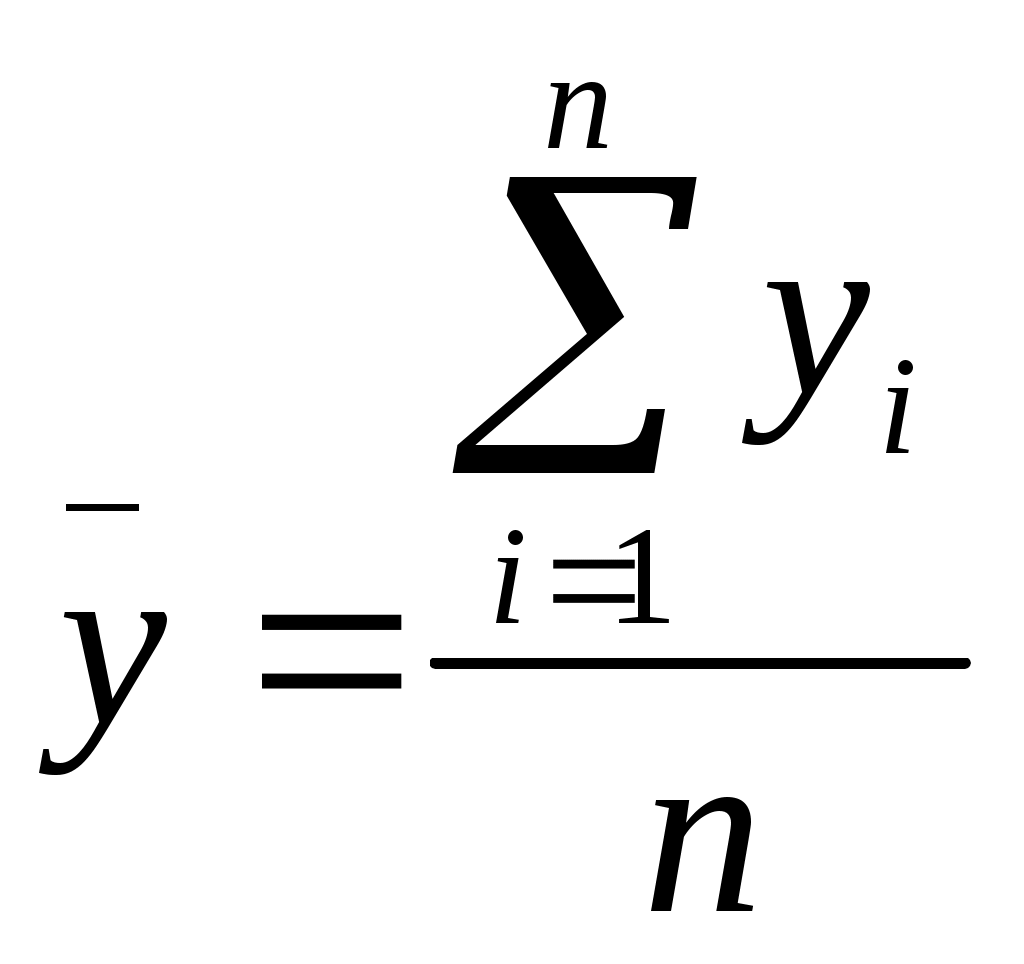 ,
, Коэффициент детерминированности ( детерминации) определяться по формуле:
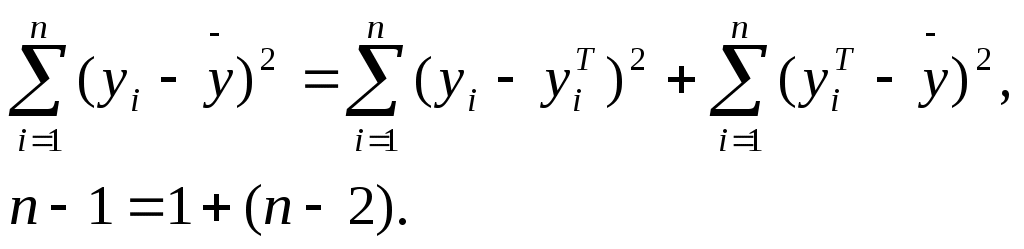 (10)
(10)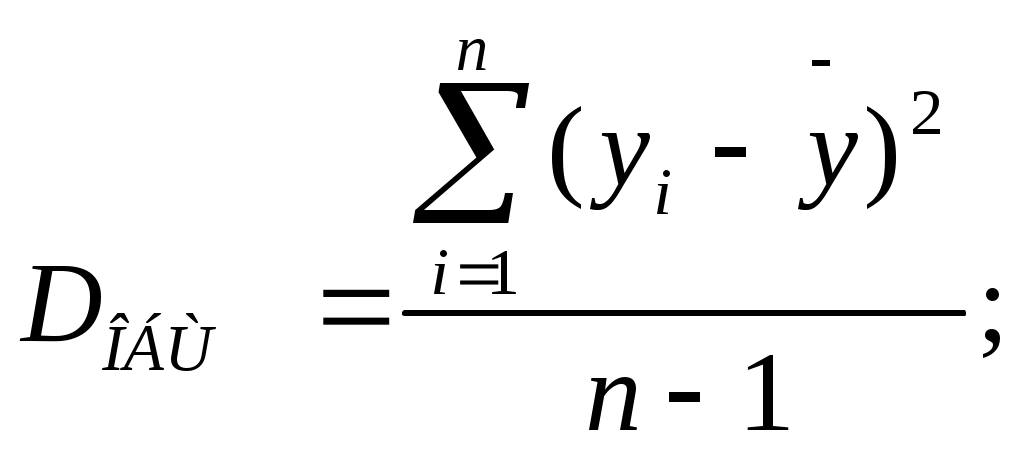 (11)
(11)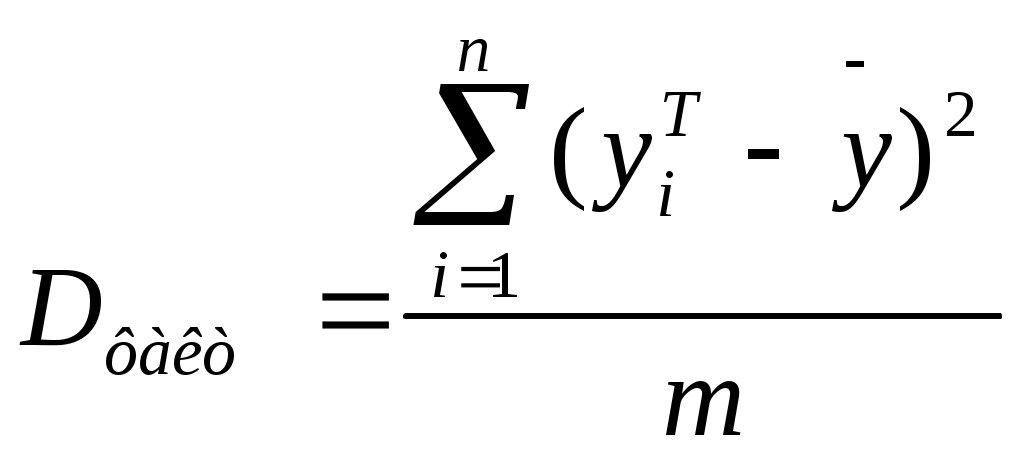 ; (12)
; (12)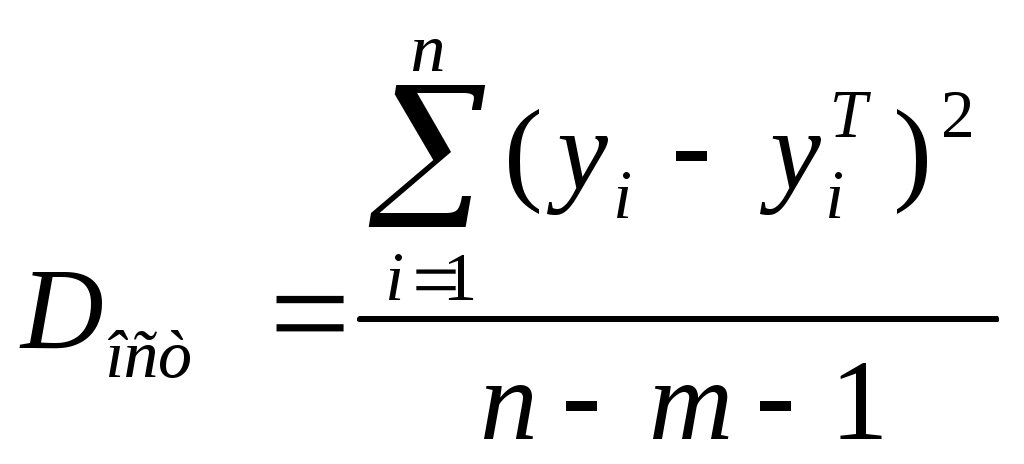 , (13)
, (13)Где m- число параметров при переменных x.
Для линейной и экспоненциальной аппроксимации m=1, для квадратичной аппроксимации m=2.
Критерий Фишера определяться соотношение:
Для линейной и экспоненциальной функции формула имеет вид:
Для параболы формула F- критерия будет :
Стандартная ошибка коэффициента регрессии
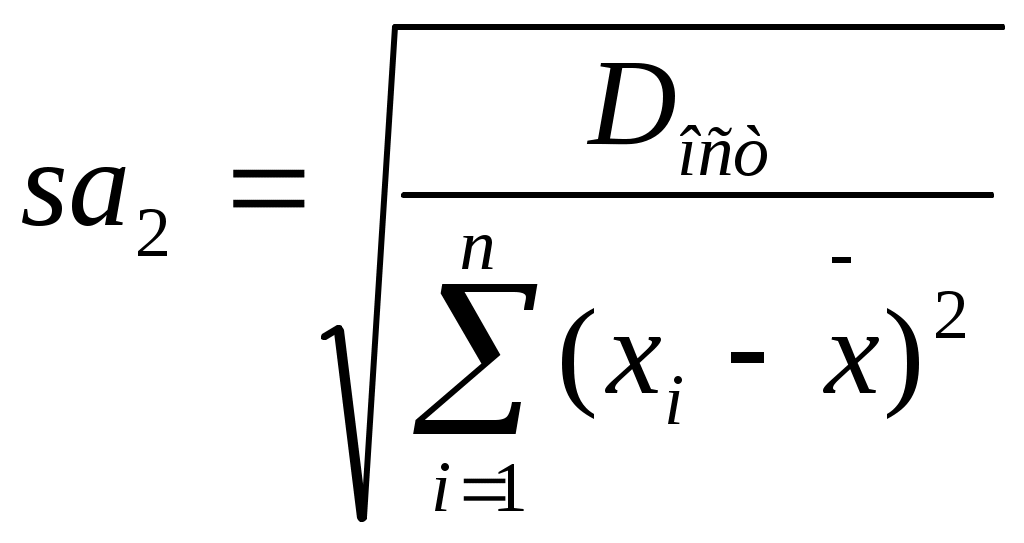 . (18)
. (18)Стандартная ошибка параметра
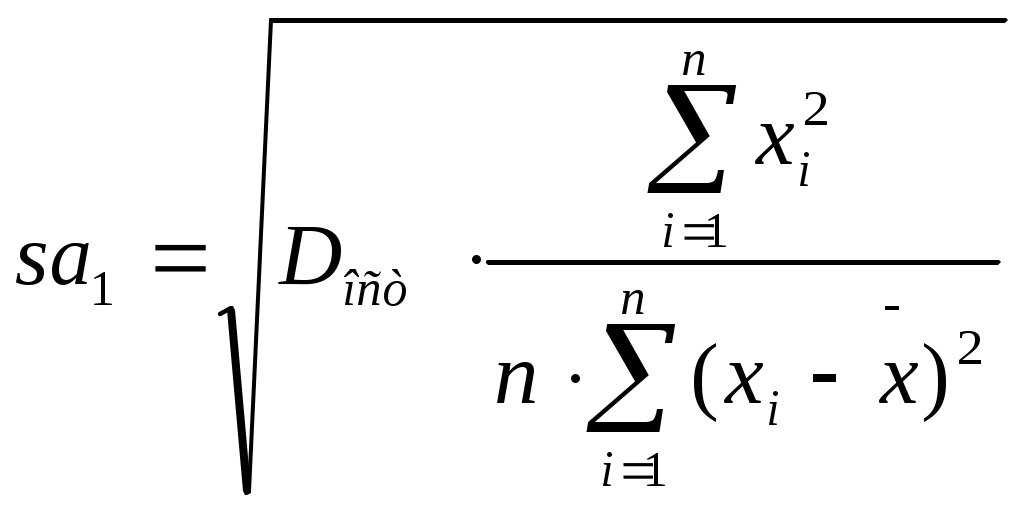 . (19)
. (19)Для оценки значимости квадратичной зависимости используется аналогичный подход. Значения стандартных ошибок вычисляются по формулам:
 (20)
(20)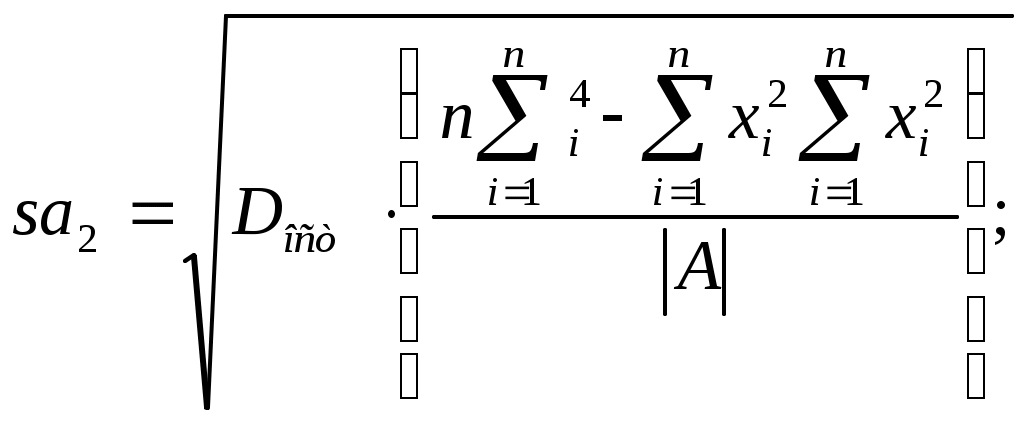 (21)
(21)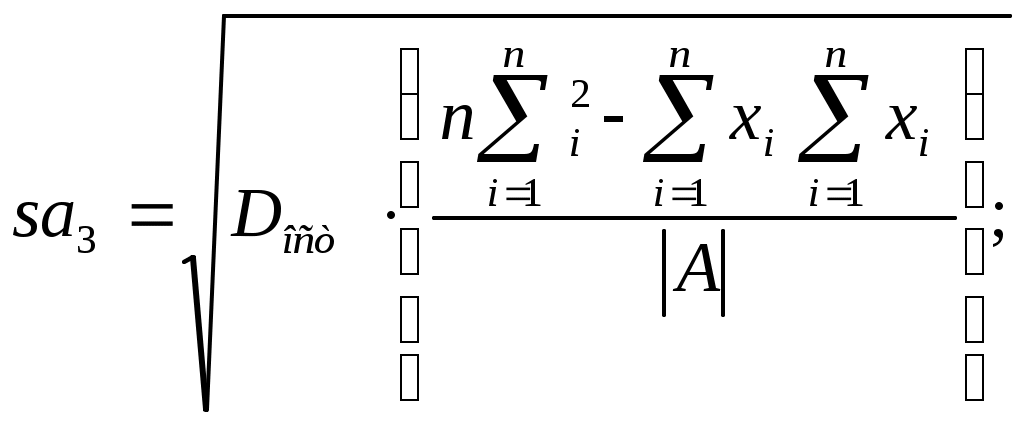
. (22)
- 1 2 3 4 5 6 7 8 9 10
Задача 1
Вариант 6
| 457,76 | 1021 |
| 777,64 | 1029 |
| 809,58 | 1037 |
| 905,52 | 1039 |
| 1141,4 | 1054 |
| 1540,28 | 1065 |
| 1773,16 | 1072 |
| 2367,92 | 1089 |
| 2292,92 | 1093 |
| 2641,8 | 1099 |
| 2803,68 | 1110 |
| 2919,68 | 1113 |
| 3256,56 | 1116 |
| 2984,56 | 1117 |
| 3276,5 | 1124 |
| 3232,44 | 1127 |
| 3285,38 | 1132 |
| 3770,32 | 1142 |
| 3993,2 | 1148 |
| 3862,26 | 1149 |
| 4150,14 | 1156 |
| 4252,08 | 1160 |
| 4023,02 | 1163 |
| 4516,96 | 1170 |
| 4662,9 | 1175 |
-
Таблицы, выполненные средствами Microsoft Excel.

Рисунок 1 вычисления вспомогательных сумм и средних значений.

Рисунок 2 - Вычисления вспомогательных сумм (продолжения).
На рис. 3 представлены расчёты для линейной аппроксимации.
| 25 | 27700 | 69697,66 | Линейная | | |
| 27700 | 30744110 | 78655052,76 | аппроксимация | ||
| | | |
| 0,9964 | |
| Обратная матрица | | | 0,99275 | ||
| 23,4196 | -0,0211 | | a1= | -27387,1153 | |
| -0,0211 | 1,9044E-05 | | a2= | 27,2338 | |
Рисунок 3 - Фрагмент рабочего листа MS Excel для линейной аппроксимации.
Таким образом уравнение линейной регрессии имеет вид:
y = 27,234x - 27387 (23)
На рис. 4 представлены расчёты для квадратичной аппроксимации.
| 25 | 27700 | 30744110 | 69697,66 | Квадратичная | |
| 27700 | 30744110 | 34179858532 | 78655053 | аппроксимация | |
| 30744110 | 3,418E+10 | 3,80616E+13 | 8,885E+10 | | |
| | | | | | 0,99276 |
| Обратная матрица | | | | ||
| 15538,5749 | -28,3153 | 0,0129 | | a1= | -24885,789 |
| -28,3153 | 0,0516 | 0,0000 | | a2= | 22,672 |
| 0,0129 | 0,0000 | 0,000000 | | a3= | 0,002 |
Рисунок 4 Фрагмент рабочего листа MS Excel для квадратичной аппроксимации
Таким образом, уравнение квадратичной регрессии имеет вид:
y = 0,0021x2 + 22,672x - 24886 (24)
На рис. 6 представлены расчёты для экспоненциальной аппроксимации.
| 25 | 27700 | 194,45 | Экспоненциальная | ||
| 27700 | 30744110 | 216145,47 |
| | |
| | | | | 0,9283 | |
| Обратная матрица | | c= | -6,88730 | ||
| 23,4196 | -0,02110 | | a2= | 0,0132 | |
| -0,0211 | 0,00002 | | a1= | 0,0010 | |
Рисунок 6 - Фрагмент листа MS Excel для экспоненциальной аппроксимации.
Таким образом, уравнение экспоненциальной регрессии имеет вид:
y = 0,001e0,0132x (25)
- 1 2 3 4 5 6 7 8 9 10