Добавлен: 03.12.2023
Просмотров: 104
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство образования и науки РФ

Национальный минерально-сырьевой университет «Горный»
Кафедра информатики и компьютерных технологий
КУРСОВАЯ РАБОТА
по дисциплине Информатика
(наименование учебной дисциплины согласно учебному плану)
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Тема: Информационные процессы в переработке нефти и газа
Построение эмпирических формул методом наименьших квадратов
Автор: студент гр. группа /Фаимлия И. О./
(шифр группы) (подпись) (Ф. И. О.)
Оценка:
Дата:
Проверил:
Руководитель работы доцент /Фамилия И. О./
(должность) (подпись) (Ф. И. О.)
Санкт-Петербург
2017
Министерство образования и науки РФ

Национальный минерально-сырьевой университет «Горный»
УТВЕРЖДАЮ
Зав. кафедрой
/ к. т. н., доц. Маховиков А. Б. /
«» 2017 г.
Кафедра информатики и компьютерных технологий
(наименование кафедры)
КУРСОВАЯ РАБОТА
по дисциплине Информатика
(наименование учебной дисциплины согласно учебному плану)
ЗАДАНИЕ
студенту группы **-12-1
(шифр группы) (Ф. И. О.)
-
Тема работы: Информационные процессы в переработке нефти и газа. Построение эмпирических формул методом наименьших квадратов -
Исходные данные к работе: Исходные данные содержатся в методических указаниях по курсовой работе -
Содержание пояснительной записки: Титульный лист, задание для выполнения работы, аннотацию, содержание, введение, текст пояснительной записки заключение, список используемой литературы -
Перечень графического материала: Рисунки, необходимые для понимания излагаемого материала -
Срок сдачи законченной работы: 10 апреля 2017 г.
Руководитель работы доцент /Фамилия И. О./
(должность) (подпись) (Ф. И. О.)
Дата выдачи задания: 20 февраля 2017 г.
Аннотация
В данной работе приведены расчеты эмпирических функций для различных зависимостей, их коэффициенты детерминированности, построены графики с наложением фактических значений.
Пояснительная записка данного проекта выполнена на 56 стр., вкл. 45 рис., библ. список из 2 наим.
Annotation
In this paper, we calculate the empirical functions for a variety of addictions, their determinism factors, the graphs with the imposition of the actual values.
Explanatory note this project is made on 56 pages, incl. 45 figures, 2 references.
Оглавление:
Введение 5
1.Расчётные формулы 7
2.Задача 1 10
2.1.Таблицы, выполненные средствами Microsoft Excel. 11
2.2. Представление результатов в виде графиков 13
2.3.Получения числовых характеристик с использованием функции ЛИНЕЙН И ЛГРФПРИБЛ 14
2.4.Аппроксимация с помощью MathCAD 16
2.5.Аппроксимация с помощью VBA 20
3.Задача 2 25
3.1.Таблицы, выполненные средствами Microsoft Excel. 26
3.2. Представление результатов в виде графиков 28
3.3.Получения числовых характеристик с использованием функции ЛИНЕЙН И ЛГРФПРИБЛ 29
3.4.Аппроксимация с помощью MathCAD 31
3.5.Аппроксимация с помощью VBA 35
4.Задача 3 41
4.1.Таблицы, выполненные средствами Microsoft Excel. 42
4.2. Представление результатов в виде графиков 44
4.3.Получения числовых характеристик с использованием функции ЛИНЕЙН И ЛГРФПРИБЛ 45
4.4.Аппроксимация с помощью MathCAD 47
4.5.Аппроксимация с помощью VBA 51
5.Вывод. 55
6. Список литературы. 56
Введение
Цель данной курсовой работы — с помощью аппроксимации установить зависимость между экспериментальными данными, решить поставленную задачу различными способами, провести расчеты с помощью табличного процессора Microsoft Excel, VBA и MathCAD.
Аппроксимация (от латинского "approximate"-"приближаться") - приближенное описание эмпирических данных с помощью уравнений, необходима для проведения интер- и экстраполяции. Задача – найти такую функцию, выраженную аналитической формулой, чтобы она наилучшим образом описывала эмпирические данные. Наиболее часто используется метод наименьших квадратов, который позволяет найти функцию с такими параметрами
, что сумма квадратов отклонений найденной функции от заданных значений функции будет минимальной.
Между величинами может существовать точная (функциональная) связь, когда одному значению аргумента соответствует одно определенное значение, и менее точная (корреляционная) связь, когда одному конкретному значению аргумента соответствует приближенное значение или некоторое множество значений функции, в той или иной степени близких друг к другу. При ведении научных исследований, обработке результатов наблюдения или эксперимента обычно приходиться сталкиваться со вторым вариантом.
При выполнении любой научно-исследовательской работы возникает проблема выявления подлинного характера зависимости изучаемых показателей. Для этого и применяется аппроксимация ― приближенное описание корреляционной зависимости переменных подходящим уравнением функциональной зависимости, передающим основную тенденцию зависимости (или ее "тренд").
При выборе аппроксимации следует исходить из конкретной задачи исследования. Важно учитывать, насколько существенны и чем обусловлены отклонения конкретных значений от получаемого тренда. При описании зависимости эмпирически определенных значений можно добиться и гораздо большей точности, используя какое-либо более сложное, много параметрическое уравнение.
Таким образом, выбирая метод аппроксимации, исследователь всегда идет на компромисс: решает, в какой степени в данном случае целесообразно и уместно «пожертвовать» деталями и, соответственно, насколько обобщенно следует выразить зависимость сопоставляемых переменных.
Специалисты в области автоматизации технологических процессов и производств имеют дело с большим объёмом экспериментальных данных, для обработки которых используется компьютер.
При рассмотрении различных задач в этой области возникает, в частности, необходимость выявления некоторых эмпирических закономерностей, решения систем уравнений, первичной статистической обработки экспериментальных данных.
Для решения многих задач, исходные данные и полученные результаты вычислений которых могут быть представлены в табличной форме, используют табличные процессоры (электронные таблицы) и, в частности, Ехсеl. Имеется также множество инженерных задач, для решения которых требуется применить язык программирования.
В данной работе использованы электронные таблицы Microsoft Excel 2007 из пакета Microsoft Office для создания контрольного варианта и построения графиков; текстовой редактор Microsoft Word 2007 для оформления отчета о проделанной работе и для построения графиков использовался MathCAD .
При выполнении работы были использованы материалы лекций и рекомендованные источники литературы.
- 1 2 3 4 5 6 7 8 9 10
Расчётные формулы
Есть разные способы оценки суммарной ошибки аппроксимации, Чаще всего оценивают суммарную квадратичную ошибку, равную сумме квадратов отклонений эмпирических значений функции от теоретических:
Эмпирическая формула:
Где
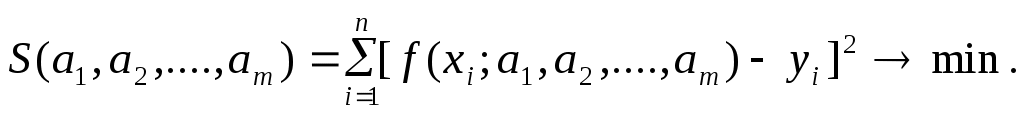 (2)
(2)Нахождения коэффициента
В случаи линейной формулы зависимости
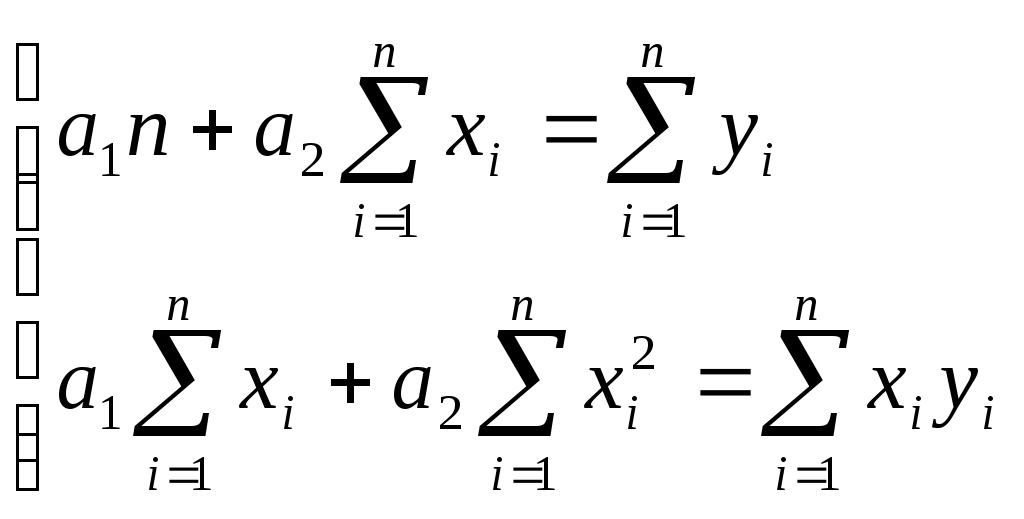 (4)
(4)В случаи квадратичной зависимости
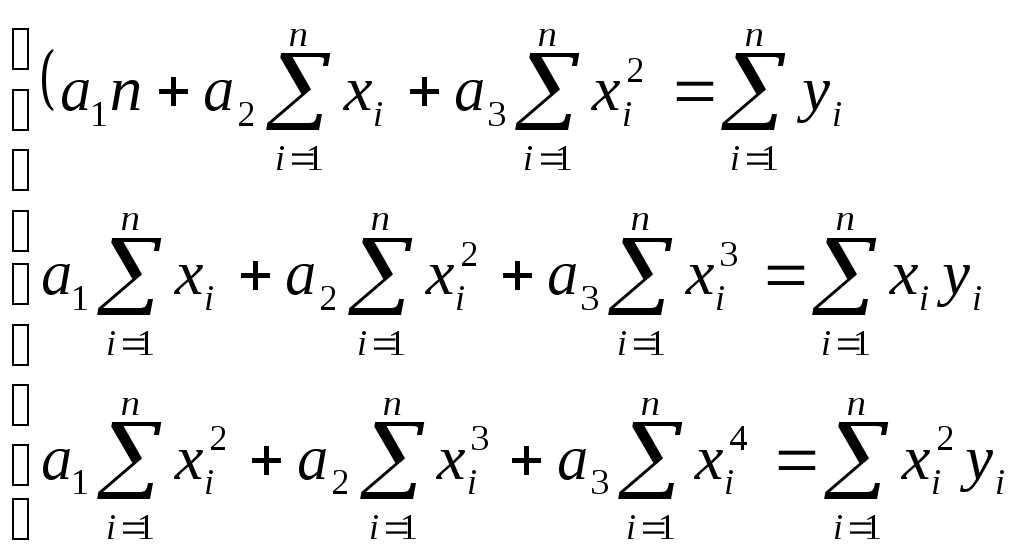 (5)
(5)Экспоненциальная зависимость :
Где
Линеаризация достигается путём логарифмирования равенства (6), после чего получим соотношение.
Коэффициент корреляции вычисляется по формуле: