Добавлен: 03.12.2023
Просмотров: 160
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Вывод. Полученные показатели говорят о том, что динамика объема инвестиций носит скачкообразный характер. Объем иностранных инвестиций в начале рассматриваемого периода возрастал, потом снижался, далее опять наблюдается рост.
Наибольший абсолютный прирост наблюдается в 2014 году по сравнению с 2013 годом, объем иностранных инвестиций вырос на 5,3 млрд. долл. США. Наибольший относительный прирост наблюдается в 2013 году по сравнению с 2012 годом, инвестиции выросли в 2,333 раза или на 133,3%.
Наибольшее снижение произошло в 2016 году по сравнению с 2015 годом, объем иностранных инвестиций снизился на 2,7 млрд. долл. США или на 22%.
В целом за рассматриваемый период объем иностранных инвестиций вырос на 11,3 млрд. долл.США. в 4,767 раза или на 376,7%.
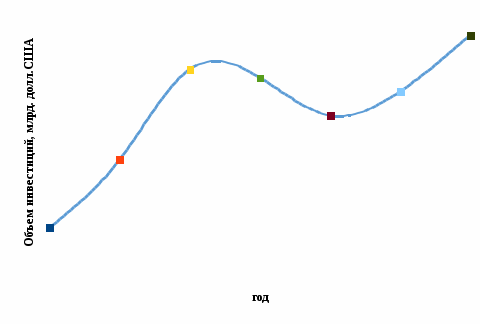
Рисунок 3 – Динамика объема иностранных инвестиций
2. Расчет средних показателей ряда динамики
Поскольку уровни ряда отражают динамику за определенные интервалы времени (годы) то ряд динамики является интервальным. Среднее значение в интервальных рядах рассчитывается по формуле средней арифметической простой:
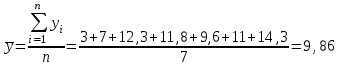 млрд. долл.США
млрд. долл.СШАСредний абсолютный прирост:
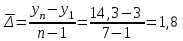 млрд. долл.США
млрд. долл.СШАСредний темп роста:
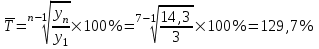
Средний темп прироста:
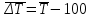 = 129,7% – 100% = 29,7%
= 129,7% – 100% = 29,7%Вывод. За рассматриваемый 7-летний период среднегодовое значение иностранных инвестиций составило 9,86 млрд. долл. США. В среднем ежегодно иностранные инвестиции возрастали на 1,8 млрд. долл.США или на 29,7%.
3. Прогноз по среднему темпу роста на три года вперед
k – период упреждения (шаг прогноза)
2019 год:
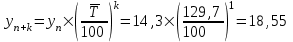 млрд. долл.США
млрд. долл.США2020 год:
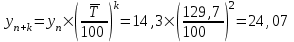 млрд. долл.США
млрд. долл.США2021 год:
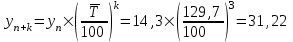 млрд. долл.США
млрд. долл.СШАВывод. Если значение среднего темпа роста не изменится
, то можно ожидать, что в2019 году объем иностранных инвестиций составит 18,55 млрд. долл.США, в 2020 году – 24,07 млрд. долл.США, в 2021 году – 31,22 млрд. долл.США.
Задача 30
Продажа товаров в розничной сети города характеризуется показателями:
Таблица 15
Показатели продажи товаров в розничной сети города
| Товар | Продано в отчетном периоде, тыс.кг | Средняя цена продажи 1 кг в отчетном периоде, руб. | Индекс розничных цен | Индекс физического объема продажи, % |
| Сахар | 270 | 82 | 2 | 90 |
| масло растительное | 120 | 87 | 1,5 | 110 |
| Масло сливочное | 150 | 250 | 1,6 | 75 |
| Мука | 60 | 53 | 1,2 | 8 |
Определите:
1) общий индекс цен по совокупности товаров;
2) общий индекс физического товарооборота;
3) общий индекс товарооборота в фактических ценах;
4) абсолютное изменение товарооборота за счет изменения цен, за счет изменения объема продаж, за счет изменения и цен, и объема продаж.
Решение:
Для расчета индексов строим вспомогательную таблицу 16.
Рассчитываем общий индекс товарооборота:
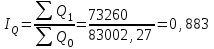
Индекс цен можно представить в форме среднегармонического индекса:
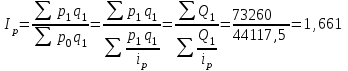
Таблица 16
Вспомогательная таблица для расчета индексов
| Товар | Продано в отчетном периоде, тыс.кг | Средняя цена продажи 1 кг в отчетном периоде, руб. | Индекс розничных цен | Индекс физического объема продажи, % | Товарооборот в отчетном периоде, тыс. руб. | Расчетная графа | Индекс товарооборота | Товарооборот в базисном периоде, тыс.руб. |
| q1 | p1 | ip | iq | Q1 | 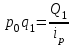 | 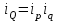 | 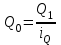 | |
| Сахар | 270 | 82 | 2 | 0,9 | 22140 | 11070,0 | 1,800 | 12300,00 |
| масло растительное | 120 | 87 | 1,5 | 1,1 | 10440 | 6960,0 | 1,650 | 6327,27 |
| Масло сливочное | 150 | 250 | 1,6 | 0,75 | 37500 | 23437,5 | 1,200 | 31250,00 |
| Мука | 60 | 53 | 1,2 | 0,08 | 3180 | 2650,0 | 0,096 | 33125,00 |
| Итого | | | | | 73260 | 44117,5 | | 83002,27 |
Индекс физического объема:
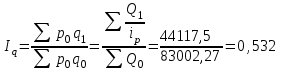
Взаимосвязь индексов:
0,883 = 1,661×0,532
Абсолютное изменение товарооборота рассчитывается, как разность числителя и знаменателя соответствующего индекса:
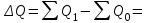 73 260 – 83 002,27 = -9 742,27 тыс. руб.
73 260 – 83 002,27 = -9 742,27 тыс. руб.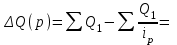 73260 – 44117,5 = 29142,5 тыс. руб.
73260 – 44117,5 = 29142,5 тыс. руб.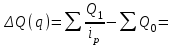 44 117,5 – 83 002,27 = -38 884,77 тыс. руб.
44 117,5 – 83 002,27 = -38 884,77 тыс. руб.Взаимосвязь абсолютных приростов:
-9742,27 = 29142,5 – 38 884,77
Вывод. В отчетном периоде по сравнению с базисным периодом товарооборот по всем товарам снизился на 11,7% или на 9742,27 тыс. руб. За счет изменения цен товарооборот вырос на 66,1% или на 29142,5 тыс. руб. А за счет изменения физического объема продаж товарооборот снизился на 46,8% или на 38 884,77 тыс. руб.
Задача 42
Для изучения тесноты связи между объемом выпуска продукции на одно предприятие и среднегодовой стоимостью основных производственных фондов по данным задачи 4 рассчитайте:
1) уравнение регрессии
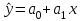 ;
;2) парный коэффициент корреляции;
3) коэффициент детерминации;
4) коэффициент эластичности.
Дайте краткий анализ полученных результатов.
Решение:
В задаче 4 отсутствуют данные об объеме выпуска продукции и среднегодовой стоимости основных фондов. В задаче 4 приведены данные по банкам об уставном капитале и активах.
Выполним задание по данным таблицы 1 (Задание 4).
Общий вид линейного уравнения парной регрессии:
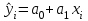
Параметры линейного уравнения найдем с помощью метода наименьших квадратов (МНК).
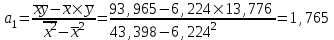
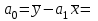 13,776 – 1,765×6,224 = 2,794
13,776 – 1,765×6,224 = 2,794Получили линейное уравнение парной регрессии:
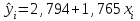
Вывод. Коэффициент регрессии показывает, что при увеличении размера уставного капитала банков на 1 ден.ед. сумма активов в среднем возрастает на 1,765 ден.ед.
Коэффициент корреляции показывает тесноту и направление линейной связи между переменными. Чем ближе значение коэффициента к единице (по модулю), тем более тесная связь между признаками.
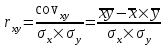
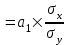 , где
, где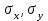 - средние квадратические отклонения признаков.
- средние квадратические отклонения признаков.Таблица 17
Вспомогательная таблица для расчета коэффициента корреляции и
построения модели
| № | 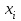 | 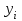 | 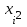 | 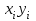 | 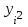 |
| 1 | 5,6 | 6,7 | 31,36 | 37,52 | 44,89 |
| 2 | 6,0 | 23,0 | 36,00 | 138,00 | 529,00 |
| 3 | 10,6 | 24,2 | 112,36 | 256,52 | 585,64 |
| 4 | 3,9 | 12,0 | 15,21 | 46,80 | 144,00 |
| 5 | 7,0 | 20,0 | 49,00 | 140,00 | 400,00 |
| 6 | 8,4 | 14,8 | 70,56 | 124,32 | 219,04 |
| 7 | 8,0 | 27,0 | 64,00 | 216,00 | 729,00 |
| 8 | 5,8 | 6,9 | 33,64 | 40,02 | 47,61 |
| 9 | 6,4 | 10,0 | 40,96 | 64,00 | 100,00 |
| 10 | 8,5 | 15,0 | 72,25 | 127,50 | 225,00 |
| 11 | 3,9 | 9,3 | 15,21 | 36,27 | 86,49 |
| 12 | 5,2 | 13,0 | 27,04 | 67,60 | 169,00 |
| 13 | 7,5 | 16,7 | 56,25 | 125,25 | 278,89 |
| 14 | 4,0 | 8,0 | 16,00 | 32,00 | 64,00 |
| 15 | 3,5 | 9,5 | 12,25 | 33,25 | 90,25 |
| 16 | 10,2 | 24,5 | 104,04 | 249,90 | 600,25 |
| 17 | 6,2 | 14,1 | 38,44 | 87,42 | 198,81 |
| 18 | 4,3 | 10,9 | 18,49 | 46,87 | 118,81 |
| 19 | 3,5 | 9,0 | 12,25 | 31,50 | 81,00 |
| 20 | 6,0 | 11,0 | 36,00 | 66,00 | 121,00 |
| 21 | 6,2 | 10,2 | 38,44 | 63,24 | 104,04 |
| 22 | 3,0 | 7,0 | 9,00 | 21,00 | 49,00 |
| 23 | 8,9 | 12,6 | 79,21 | 112,14 | 158,76 |
| 24 | 9,0 | 14,0 | 81,00 | 126,00 | 196,00 |
| 25 | 4,0 | 15,0 | 16,00 | 60,00 | 225,00 |
| Итого | 155,60 | 344,4 | 1084,96 | 2349,12 | 5565,48 |
| Среднее | 6,224 | 13,776 | 43,398 | 93,965 | 222,619 |