Добавлен: 03.12.2023
Просмотров: 159
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
;
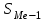– сумма частот, накопившихся до начала медианного интервала.
Медианным интервалом является интервал 130-160, так как именно в этом интервале накопленная частота S2 =230 впервые превышает величину, равную половине совокупности (0,5·450 = 225).
Расчет медианы:
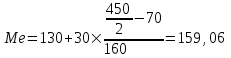
Вывод. В рассматриваемой совокупности половина автомобилей имеют среднесуточный пробег не менее 159,06 км, а другая половина – не более 159,06 км.
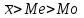, следовательно, асимметрия правосторонняя. В совокупности преобладают автомобили с более низкими значениями признака, чем среднее значение.
3. Расчет показателей вариации
Размах вариации характеризует амплитуду колебаний значений признака, рассчитывается как разность максимального и минимального значения признака:
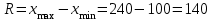
Среднее линейное отклонение показывает, насколько в среднем отклоняются конкретные варианты признака от среднего значения. Взвешенное среднее линейное отклонение:
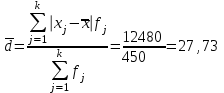
Дисперсия представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины. Для интервального ряда используется формула взвешенной дисперсии:
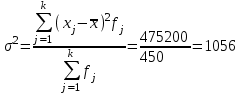
Среднее квадратическое отклонение также как и среднее линейное отклонение показывает, насколько в среднем отклоняются конкретные варианты признака от среднего значения. Однако является более точной характеристикой. Рассчитывается, как корень квадратный из дисперсии:
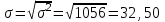
Вывод. Отклонение от среднего значения среднесуточного пробега в ту или иную сторону составляет 32,50 км.
Коэффициент вариации является мерой относительной колеблемости признака около средней и характеризует степень однородности признака в изучаемой совокупности:
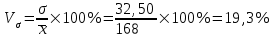
Вывод. Значение коэффициента вариации не превышает 33,3%, следовательно, вариация признака в исследуемой совокупности единиц незначительная и совокупность однородна. Найденное среднее значение среднесуточного пробега является типичной и надежной характеристикой среднего.
Относительное линейное отклонение
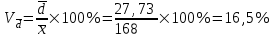
Коэффициент осцилляции:
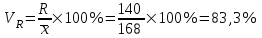
Вывод. Доля среднего линейного отклонения в среднем значении среднесуточного пробега составляет 16,5%. Доля размаха вариации в среднем значении – 83,3%.
Для характеристики уровня жизни населения в районе проведена 5%-ная пропорциональная типическая выборка с механическим отбором домашних хозяйств, в результате которой получены следующие данные:
Таблица 12
Результаты 5%-ной пропорциональной типической выборки с механическим отбором домашних хозяйств
Определите с вероятностью 0,997 границы, в которых находится доля населения района с доходами ниже прожиточного минимума.
Решение:
Определим общую среднюю долю домохозяйств с доходами ниже величины прожиточного минимума в обоих типах домохозяйств:
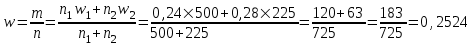
Предельная ошибка выборки для доли при типической выборке с бесповторным отбором определяется по формуле:
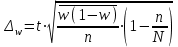, где
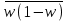- внутригрупповая дисперсия доли;
n – объем выборочной совокупности;
N– объем генеральной совокупности;
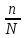- доля выборки;
t – коэффициент доверия, зависящий от вероятности Р, с которой можно гарантировать определенные размеры предельной ошибки.
Значения t вычислены заранее для различных доверительных вероятностей Р и протабулированы (таблицы функции Лапласа). При доверительной вероятности Р = 0,997 коэффициент доверия t = 3,0.
По условию, выборка 5%-ная, следовательно,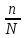 = 0,05.
Внутригрупповая дисперсия доли домохозяйств с доходами ниже величины прожиточного минимума:
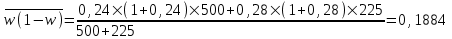
Расчет предельной ошибки выборки для доли:
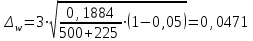
Предельная ошибка выборки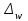
определяет границы, в пределах которых будет находиться генеральная доля р единиц, обладающих заданным свойством:
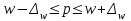
Определение доверительного интервала генеральной доли:
0,2524 – 0,0471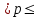
0,0224 + 0,0471
0,2053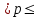 0,2995
20,53%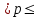 29,95
Вывод. С вероятностью 0,997 можно утверждать, что в генеральной совокупности домохозяйств доля домохозяйств доходами ниже величины прожиточного минимума будет находиться в пределах от 20,53% до 29,95%.
Динамика иностранных инвестиций в экономику России характеризуется следующими данными, млрд. долл. США:
Таблица 13
Данные о динамике иностранных инвестиций в экономику России
Для анализа динамики поступления иностранных инвестиций в экономику России в 2012–2018 гг. вычислите:
1) абсолютные приросты, темпы роста и прироста по годам и относительно 2012 года; абсолютное содержание одного процента прироста. Полученные показатели представьте в табличной форме, постройте график динамики объема иностранных инвестиций в экономику Росси в 2012–2018 гг.;
2) среднегодовое поступление иностранных инвестиций в экономику России;
3) среднегодовой темп роста и темп прироста поступления иностранных инвестиций;
4) ожидаемое поступление иностранных инвестиций на три года вперед при условии сохранения среднегодового темпа роста.
Сделайте выводы.
Решение:
1. Расчет цепных и базисных показателей ряда динамики
Если сравнение происходит с предыдущим годом, то показатель называется цепным. Если с постоянной базой (2012 год), то базисный.
Абсолютный прирост рассчитывается по формулам:
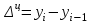
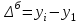
yi– значение показателя в анализируемый год;
yi-1 – значение показателя в год, предшествующий анализируемому;
у1 – значение показателя в 2012 году.
Темп роста рассчитывается по формулам:
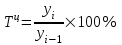
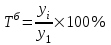
Темп прироста рассчитывается по формулам:
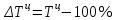
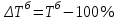
Абсолютное значение 1% прироста определяется по формуле:
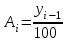
Рассчитывается только по цепным показателям.
Расчет показателей представлен в таблице 14.
Таблица 14
Расчет показателей ряда динамики
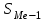– сумма частот, накопившихся до начала медианного интервала.Медианным интервалом является интервал 130-160, так как именно в этом интервале накопленная частота S2 =230 впервые превышает величину, равную половине совокупности (0,5·450 = 225).
Расчет медианы:
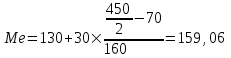
Вывод. В рассматриваемой совокупности половина автомобилей имеют среднесуточный пробег не менее 159,06 км, а другая половина – не более 159,06 км.
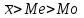, следовательно, асимметрия правосторонняя. В совокупности преобладают автомобили с более низкими значениями признака, чем среднее значение.3. Расчет показателей вариации
Размах вариации характеризует амплитуду колебаний значений признака, рассчитывается как разность максимального и минимального значения признака:
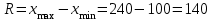
Среднее линейное отклонение показывает, насколько в среднем отклоняются конкретные варианты признака от среднего значения. Взвешенное среднее линейное отклонение:
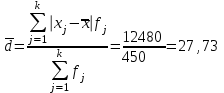
Дисперсия представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины. Для интервального ряда используется формула взвешенной дисперсии:
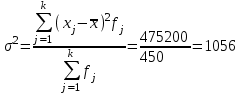
Среднее квадратическое отклонение также как и среднее линейное отклонение показывает, насколько в среднем отклоняются конкретные варианты признака от среднего значения. Однако является более точной характеристикой. Рассчитывается, как корень квадратный из дисперсии:
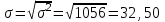
Вывод. Отклонение от среднего значения среднесуточного пробега в ту или иную сторону составляет 32,50 км.
Коэффициент вариации является мерой относительной колеблемости признака около средней и характеризует степень однородности признака в изучаемой совокупности:
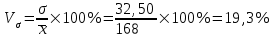
Вывод. Значение коэффициента вариации не превышает 33,3%, следовательно, вариация признака в исследуемой совокупности единиц незначительная и совокупность однородна. Найденное среднее значение среднесуточного пробега является типичной и надежной характеристикой среднего.
Относительное линейное отклонение
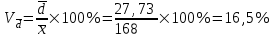
Коэффициент осцилляции:
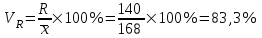
Вывод. Доля среднего линейного отклонения в среднем значении среднесуточного пробега составляет 16,5%. Доля размаха вариации в среднем значении – 83,3%.
Задача 23
Для характеристики уровня жизни населения в районе проведена 5%-ная пропорциональная типическая выборка с механическим отбором домашних хозяйств, в результате которой получены следующие данные:
Таблица 12
Результаты 5%-ной пропорциональной типической выборки с механическим отбором домашних хозяйств
| тип домохозяйства | Число обследованных домохозяйств | Доля домохозяйств с доходами ниже прожиточного минимума, % |
| В городской местности | 500 | 24 |
| В сельской местности | 225 | 28 |
Определите с вероятностью 0,997 границы, в которых находится доля населения района с доходами ниже прожиточного минимума.
Решение:
Определим общую среднюю долю домохозяйств с доходами ниже величины прожиточного минимума в обоих типах домохозяйств:
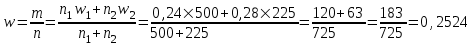
Предельная ошибка выборки для доли при типической выборке с бесповторным отбором определяется по формуле:
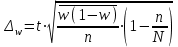, где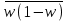 - внутригрупповая дисперсия доли;n – объем выборочной совокупности;
N– объем генеральной совокупности;
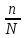- доля выборки;t – коэффициент доверия, зависящий от вероятности Р, с которой можно гарантировать определенные размеры предельной ошибки.
Значения t вычислены заранее для различных доверительных вероятностей Р и протабулированы (таблицы функции Лапласа). При доверительной вероятности Р = 0,997 коэффициент доверия t = 3,0.
По условию, выборка 5%-ная, следовательно,
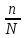= 0,05.Внутригрупповая дисперсия доли домохозяйств с доходами ниже величины прожиточного минимума:
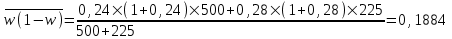
Расчет предельной ошибки выборки для доли:
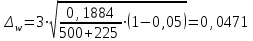
Предельная ошибка выборки
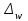определяет границы, в пределах которых будет находиться генеральная доля р единиц, обладающих заданным свойством: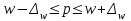 Определение доверительного интервала генеральной доли:
0,2524 – 0,0471
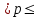0,0224 + 0,04710,2053
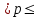0,299520,53%
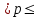29,95Вывод. С вероятностью 0,997 можно утверждать, что в генеральной совокупности домохозяйств доля домохозяйств доходами ниже величины прожиточного минимума будет находиться в пределах от 20,53% до 29,95%.
Задача 27
Динамика иностранных инвестиций в экономику России характеризуется следующими данными, млрд. долл. США:
Таблица 13
Данные о динамике иностранных инвестиций в экономику России
| годы | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
| Всего инвестиций | 3 | 7 | 12,3 | 11,8 | 9,6 | 11 | 14,3 |
Для анализа динамики поступления иностранных инвестиций в экономику России в 2012–2018 гг. вычислите:
1) абсолютные приросты, темпы роста и прироста по годам и относительно 2012 года; абсолютное содержание одного процента прироста. Полученные показатели представьте в табличной форме, постройте график динамики объема иностранных инвестиций в экономику Росси в 2012–2018 гг.;
2) среднегодовое поступление иностранных инвестиций в экономику России;
3) среднегодовой темп роста и темп прироста поступления иностранных инвестиций;
4) ожидаемое поступление иностранных инвестиций на три года вперед при условии сохранения среднегодового темпа роста.
Сделайте выводы.
Решение:
1. Расчет цепных и базисных показателей ряда динамики
Если сравнение происходит с предыдущим годом, то показатель называется цепным. Если с постоянной базой (2012 год), то базисный.
Абсолютный прирост рассчитывается по формулам:
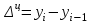
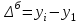
yi– значение показателя в анализируемый год;
yi-1 – значение показателя в год, предшествующий анализируемому;
у1 – значение показателя в 2012 году.
Темп роста рассчитывается по формулам:
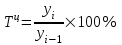
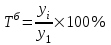
Темп прироста рассчитывается по формулам:
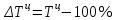
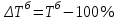
Абсолютное значение 1% прироста определяется по формуле:
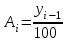
Рассчитывается только по цепным показателям.
Расчет показателей представлен в таблице 14.
Таблица 14
Расчет показателей ряда динамики
| год | Объем инвестиций, млрд. долл. США | Абсолютный прирост, млрд. долл. США | темп роста,% | темп прироста, % | Абсолютное содержание 1% прироста, млрд. долл. США | |||||
| цепной | базисный | цепной | базисный | цепной | базисный | |||||
| 2012 | 3,0 | - | - | - | - | - | - | - | ||
| 2013 | 7,0 | 4,0 | 4,0 | 233,3 | 233,3 | 133,3 | 133,3 | 0,030 | ||
| 2014 | 12,3 | 5,3 | 9,3 | 175,7 | 410,0 | 75,7 | 310,0 | 0,070 | ||
| 2015 | 11,8 | -0,5 | 8,8 | 95,9 | 393,3 | -4,1 | 293,3 | 0,123 | ||
| 2016 | 9,6 | -2,7 | 6,6 | 78,0 | 320,0 | -22,0 | 220,0 | 0,123 | ||
| 2017 | 11,0 | 1,4 | 8,0 | 114,6 | 366,7 | 14,6 | 266,7 | 0,096 | ||
| 2018 | 14,3 | 3,3 | 11,3 | 130,0 | 476,7 | 30,0 | 376,7 | 0,110 | ||