Добавлен: 03.12.2023
Просмотров: 165
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
На основе групповых строк «Всего» таблицы 6 строим интервальный ряд распределения (таблица 7).
Таблица 7
Интервальный ряд распределения банков по сумме активов
| Группы банков по сумме активов, ден.ед. | Число банков, единиц | Число банков в % к итогу | накопленная частота | накопленная относительная частота, % |
| 6,70-10,76 | 9 | 36 | 9 | 36 |
| 10,76-14,82 | 8 | 32 | 17 | 68 |
| 14,82-18,88 | 3 | 12 | 20 | 80 |
| 18,88-22,94 | 1 | 4 | 21 | 84 |
| 22,94-27,00 | 4 | 16 | 25 | 100 |
| Итого | 25 | 100 | - | - |
Вывод. Построенная группировка говорит о том, что распределение банков по сумме активов не является равномерным, преобладают банки с суммой активов от 6,7 до 10,76 ден.ед., это 9 банков доля которых составляет 36% от общего числа рассматриваемых банков.
Доля банков в наибольшей суммой активов (от 22,94 до 27 ден.ед.) составляет 16% (4 банка). наименее часто встречаются банки с суммой активов от 18,88 дол 22,94 ден.ед. (1 банк или 4% от общего числа банков).
80% банков имеют сумму активов не менее, чем 18,88 ден.ед.
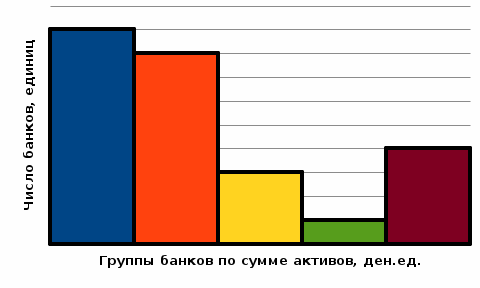
Рисунок 2 – Гистограмма распределения банков по сумме активов
3. Корреляционная таблица
Для построения корреляционной таблицы используем группировки по факторному (уставный капитал) и результативному признаку (сумма активов). Подсчитываем частоты по обоим признакам.
Таблица 8
Корреляционная таблица
| Группы банков по размеру уставного капитала, ден.ед. | Группы банков по сумме активов, ден.ед. | Итого | |||||
| 6,70-10,76 | 10,76-14,82 | 14,82-18,88 | 18,88-22,94 | 22,94-27,00 | |||
| 3,00-4,52 | 5 | 2 | 1 | | | 8 | |
| 4,52-6,04 | 2 | 2 | | | 1 | 5 | |
| 6,04-7,56 | 2 | 1 | 1 | 1 | | 5 | |
| 7,56-9,08 | | 3 | 1 | | 1 | 5 | |
| 9,08-10,6 | | | | | 2 | 2 | |
| Итого | 9 | 8 | 3 | 1 | 4 | 25 | |
Вывод. Распределение частот в корреляционной таблице произошло из левого верхнего угла в правый нижний угол. Это говорит о наличии прямой корреляционной связи между признаками. Т.е. с увеличением размера уставного капитала банков сумма активов тоже в среднем увеличивается.
4. Построение аналитической группировки
При использовании метода аналитической группировки строится интервальный ряд распределения единиц совокупности по факторному признаку Х и для каждой группы ряда определяется среднегрупповое значение
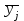 результативного признака Y.
результативного признака Y. Если с ростом значений фактора Х от группы к группе среднегрупповые значения
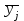 систематически возрастают (или убывают), между признаками X и Y имеет место корреляционная связь.
систематически возрастают (или убывают), между признаками X и Y имеет место корреляционная связь.Результативный признак Y – активы. Факторный признак Х – уставный капитал.
Группировка по размеру уставного капитала была произведена в п. 1 задания. Групповые значения суммы активов берем из итоговых строк «Всего» таблицы 3.
Таблица 9
Аналитическая группировка зависимости суммы активов от величины уставного капитала банков
| Группы банков по размеру уставного капитала, ден.ед. | Число банков в группе | Активы, ден.ед. | |
| Всего | В среднем на 1 банк 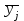 | ||
| 1 | 2 | 3 | 4=3/2 |
| 3,00-4,52 | 8 | 80,7 | 10,09 |
| 4,52-6,04 | 5 | 60,6 | 12,12 |
| 6,04-7,56 | 5 | 71,0 | 14,20 |
| 7,56-9,08 | 5 | 83,4 | 16,68 |
| 9,08-10,6 | 2 | 48,7 | 24,35 |
| Итого | 25 | 344,4 | 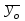 = 13,78 = 13,78 |
Вывод. Анализ 1-го и последнего столбца таблицы 3 показывает, что с увеличением размера уставного капитала происходит систематическое увеличение средней суммы активов на 1 банк по каждой группе банков (с 10,09 до 24,35 ден.ед.). Это говорит о наличии прямой корреляционной зависимости между признаками.
Задача 9
По данным выборочного наблюдения распределение автомобилей по величине суточного пробега характеризуется следующими данными:
Таблица 10
Данные о распределении автомобилей по величине суточного пробега
| Суточный пробег, км | Число автомобилей |
| 100 – 130 | 70 |
| 130 – 160 | 160 |
| 160 – 190 | 120 |
| 190 – 210 | 80 |
| 210 – 240 | 20 |
Определите:
1) средний суточный пробег одного автомобиля;
2) моду, медиану (аналитически и графически);
3) показатели вариации;
По результатам расчетов сделайте выводы.
Решение:
1. Расчет среднесуточного пробега
Для расчета показателей строим вспомогательную таблицу 11.
Для расчета среднего в интервальном ряду используется формула средней арифметической взвешенной:
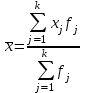 , где
, гдеxj– середина j-го интервала;
fj– частота j-го интервала.
Таблица 1
Вспомогательная таблица для расчета показателей распределения
| Суточный пробег, км | Число автомобилей 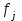 | Середина интервала 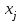 | 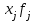 | 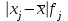 | 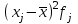 | Накопленная частота |
| 100 – 130 | 70 | 120 | 8400 | 3360 | 161280 | 70 |
| 130 – 160 | 160 | 150 | 24000 | 2880 | 51840 | 230 |
| 160 – 190 | 120 | 180 | 21600 | 1440 | 17280 | 350 |
| 190 – 210 | 80 | 210 | 16800 | 3360 | 141120 | 430 |
| 210 – 240 | 20 | 240 | 4800 | 1440 | 103680 | 450 |
| Итого | 450 | | 75600 | 12480 | 475200 | |
Расчет средней арифметической взвешенной:
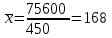 км
кмВывод. В рассматриваемой совокупности автомобилей среднее значение суточного пробега составляет 168 км.
2. Расчет моды и медианы
Мода и медиана являются структурными средними величинами, характеризующими (наряду со средней арифметической) центр распределения единиц совокупности по изучаемому признаку.
Мода Мо – значение признака, которое встречается наиболее часто в рассматриваемой совокупности. В интервальном вариационном ряду модой приближенно считается центральное значение модального интервала (имеющего наибольшую частоту).
Конкретное значение моды для интервального ряда рассчитывается по формуле:
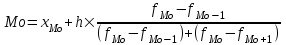 , где
, гдехМo – нижняя граница модального интервала,
h – величина модального интервала,
fMo– частота модального интервала,
fMo-1 – частота интервала, предшествующего модальному,
fMo+1 – частота интервала, следующего за модальным.
Согласно данным модальным интервалом ряда является интервал 130-160, так как его частота максимальна (f2= 160).
Расчет моды:
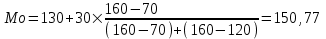
Вывод. Для рассматриваемой совокупности наиболее часто встречаются автомобили со среднесуточным пробегом 150,77 км.
Медиана Ме – это значение признака, приходящееся на середину ранжированного ряда. По обе стороны от медианы находится одинаковое количество единиц совокупности.
Конкретное значение медианы для интервального ряда рассчитывается по формуле:
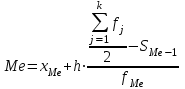 , где
, где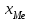 – нижняя граница медианного интервала,
– нижняя граница медианного интервала,h – величина медианного интервала;
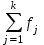 – сумма всех частот ряда;
– сумма всех частот ряда;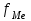 – частота медианного интервала
– частота медианного интервала