Файл: Теория оптимизации.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 04.12.2023

Просмотров: 111

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

ВВЕДЕНИЕ

Перейти.

ЛАБОРАТОРНАЯ РАБОТА №1

Максимальное время

Предельное число итераций

Относительная погрешность

Допустимое отклонение

Сходимость

Линейная модель

Показывать результаты итераций

Автоматическое масштабирование

Значения не отрицательны

Параметрический анализ

ПРИМЕР РЕШЕНИЯ ЗАДАЧИ СИМПЛЕКС-МЕТОДОМ (ВАРИАНТ1)

ЛАБОРАТОРНАЯ РАБОТА №2




МЕТОДИЧЕСКИЕ УКАЗАНИЯ
К ВЫПОЛНЕНИЮ ЛАБОРАТОРНЫХ РАБОТ 1-2
ПО ДИСЦИПЛИНЕ “ТЕОРИЯ ОПТИМИЗАЦИИ И ПРИНЯТИЯ РЕШЕНИЙ”

ВВЕДЕНИЕ




Лабораторные работы предполагают решение задач оптимизации с использованием надстройки “Поиск решения” Microsoft EXCEL.
Доступ к инструменту Поиск решения осуществляется с помощью команды Данные Анализ Поиск решения

Если команда Поиск решения или группа Анализ отсутствует на вкладке

Данные, то необходимо загрузить соответствующую надстройку:

  1. Выбрать команду Файл Параметры.

  2. В диалоговом окне Параметры Ехсеl выбрать категорию Надстройки






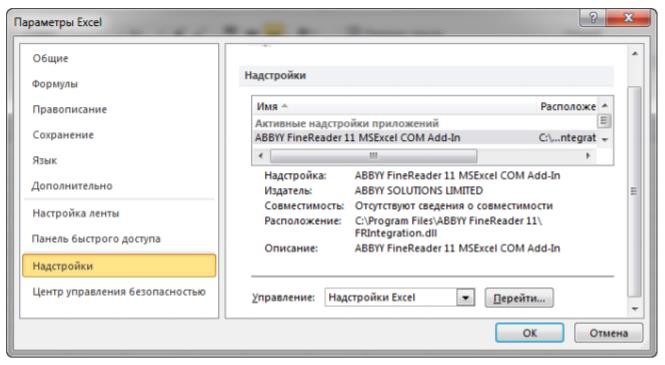
  1. В поле Управление выбрать значение Надстройки Excel, затем кнопку

Перейти.


  1. В поле Доступные надстройки установить флажок рядом с пунктом

Поиск решения и нажать кнопку ОК.

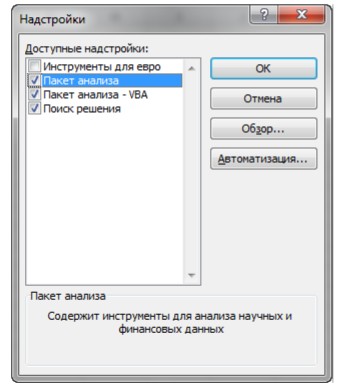
После выполнения этих действий команда Поиск решения будет доступной в группе команд Анализ вкладки Данные.

В
методических указаниях подробно рассмотрены основные этапы решения задач с использованием версии Microsoft EXCEL 2007. В других версиях решение осуществляется аналогично.

ЛАБОРАТОРНАЯ РАБОТА №1


РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОЙ ОПТИМИЗАЦИИ СРЕДСТВАМИ EXCEL
Цельработы: Получение практических навыков формирования математических моделей прикладных задач линейного программирования и их решения средствами EXCEL.
Лабораторныезадания.

  1. По лекциям и учебному пособию ознакомиться с постановкой и методами решения задач линейной оптимизации (ГЛАВА 3, п. 3.1-3.4.).

  2. Выбрать задачу в соответствии с вариантом, составить ее математическую модель и решить с использованием средств EXCEL. Сформировать отчеты по устойчивости, результатам и пределам. Для визуализации результатов решения построить диаграммы. Проанализировать полученные результаты.

  3. Провести параметрический анализ решая задачу при пяти различных значениях ресурса оборудования первого типа (варианты 1-3), второго типа (варианты 4-7) и третьего типа (варианты 8-10).

  1. Решить задачу вручную с использованием симплекс-метода и графического метода. (Графический метод изложен в п.3.3.1 учебного пособия, симплекс-метод – в п.3.3.2)

  2. Сравнить результаты, полученные при выполнении лабораторных заданий 1 и 2.



Отчетполабораторной работе должен содержать :

  1. Постановку задачи.

  2. Математическую оптимизационную модель.

  3. Краткое описание основных этапов решения в среде EXCEL.

  4. Результат решения задачи (итоговую таблицу в EXCEL).

  5. Отчеты по результатам, устойчивости, пределам.

  6. Построенные диаграммы.

  7. Результаты параметрического анализа с соответствующими выводами.

  8. Решение задачи вручную с использованием симплекс-метода и графического метода.

  9. Выводы.


Для производства двух видов изделий A и B используются три типа технологического оборудования. Для производства одного изделия A оборудование первого типа используется в течение a1 часов, оборудование второго типа – a2 часов, оборудование третьего типа – a3 часов. Для производства одного изделия B оборудование первого типа
используется в течение b1 часов, оборудование второго типа – b2 часов, оборудование третьего типа – b3 часов. На изготовление всех изделий предприятие может использовать оборудование

первого типа не более чем t1 часов, оборудование второго типа – не более t2 часов, оборудование третьего типа – не более t3 часов. Прибыль от реализации одного готового изделия A составляет денежных единиц, а изделия В - денежных единиц. Составить план производства изделий A и B, обеспечивающий максимальную прибыль от их реализации.


Вариант
a1
a2
a3
b1
b2
b3
t1
t2
t3




1
1
1
3
1
2
1
20
36
40
2
5

2
2
1
3
2
2
1
40
34
46
1
2

3
3
1
3
3
2
1
60
32
50
1
3

4
1
1
3
1
2
1
24
40
52
2
4

5
2
1
3
2
2
1
48
38
56
2
6

6
3
2
1
1
2
2
40
40
36
2
1

7
3
1
1
1
2
1
46
34
20
5
2

8
1
3
3
2
3
1
32
60
50
4
2

9
1
3
1
2
1
1
40
52
24
6
2

10
3
2
1
1
2
2
56
48
38
3
1



Методическиеуказаниядля выполнения работы
Решение задач в среде EXCEL начинается с ввода условий задачи. Ввод условий задачи состоит из следующих основных шагов:

  • создание формы для ввода условий задачи;

  • ввод исходных данных;

  • ввод зависимостей из математической модели;

  • назначение целевой функции;

  • ввод ограничений и граничных условий.

Последовательность работ рассмотрим на примере задачи составления производственного плана.

Пусть требуется определить, в каком количестве необходимо выпускать продукцию четырех типов Прод1, Прод2, Прод3, Прод4 для изготовления которой требуются ресурсы трех видов: трудовые ресурсы, сырье, финансы. Нормы расхода ресурсов каждого вида для выпуска единицы продукции, а также прибыль, получаемая от реализации единицы каждого типа продукции, приведены в табл. 1. Количество расходуемых ресурсов не должно превышать имеющихся запасов.
Таблица 1

Ресурсы



Виды продукции



Запасы ресурсов




Прод. 1
Прод. 2
Прод.3
Прод.4



Трудовые
3
1
2
4
440

Сырье
1
8
6
2
200

Финансы
1
4
7
2
320

Прибыль
7
3
6
12


Смотрите также файлы