ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 109
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Параметрический анализ
Под параметрическим анализом будем понимать решение задачи оптимизации при различных значениях того параметра, который ограничивает улучшение целевой функции.
Параметрический анализ будем выполнять для рассматриваемой задачи производственного планирования, решая её при различных значениях имеющегося сырья. Составим таблицу вариантов:
| Вариант | 1 | 2 | 3 | 4 | 5 |
| Сырье | 100 | 150 | 200 | 250 | 300 |
Для выполнения параметрических расчетов в таблице с результатами решения задачи (рис.8) необходимо удалить результат решения, находящийся в ячейках B3:E3. Далее решить задачу для первого варианта по описанной выше схеме, предварительно введя в ячейку H10 значение 100. После решения задачи в диалоговом окне Результаты поиска решения выбирается команда Сохранить сценарий. При этом на экране появится
диалоговое окно Сохранение сценария (рис. 16). В появившемся диалоговом окне необходимо ввести имя сценария “Сырье=100” и подтвердить ввод выбором кнопки OK.
Рис. 16
Результат решения задачи для данного варианта представлен на рис. 17.
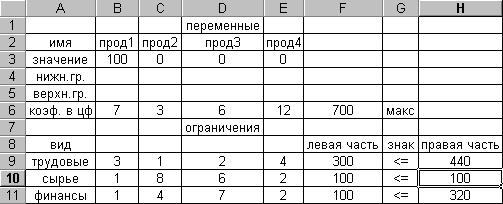
Рис. 17
Далее необходимо аналогично решить задачу для всех оставшихся вариантов, последовательно вводя в ячейку H10 значения 150, 200, 250, 300. При этом нужно сохранять каждый сценарий и вводить его имя, соответствующее текущему значению сырья.
Для представления результатов решения вызывается пункт меню Данные, Анализ “Что-Если” и в появившемся диалоговом окне Диспетчер сценариев (рис. 18) выбирается пункт Отчет.
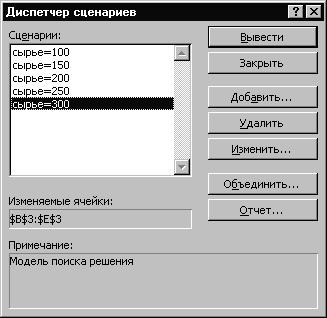
Рис. 19
При выборе в диалоговом окне Отчет по сценарию (рис.20) типа отчета Структура
создается итоговый сценарий (рис.21), который размещается на отдельном листе с названием “Структура сценария”.
Рис. 20
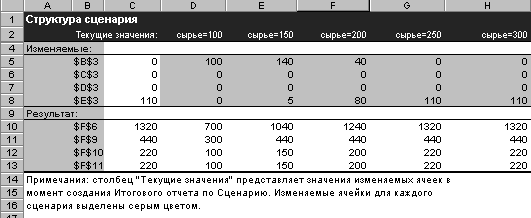
Рис. 21
Для удобства дальнейшей работы полученный сценарий можно отредактировать и представить следующем виде:
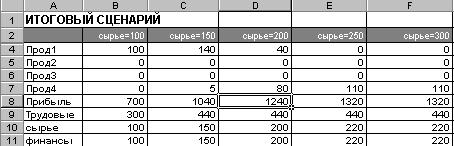
Рис. 22
Для наглядного представления результатов построим гистограммы:
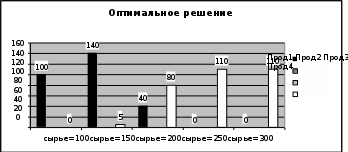
Рис. 23
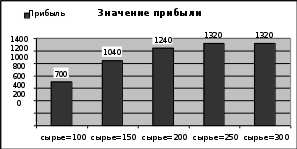
Рис.24.
ПРИМЕР РЕШЕНИЯ ЗАДАЧИ СИМПЛЕКС-МЕТОДОМ (ВАРИАНТ1)
Математическая модель
F 2x1 5x2 max
x1 x2 20
x1 2x2 36
3x1 x2 40
x1, x2 0
Каноническая форма:
F 2x1 5x2 min
x1 x2 x3 20
x1 2x2 x4 36
3x1 x2 x5 40
x1, x2 , x3, x4 , x5 0
Решение иллюстрируется симплекс-таблицей:
| xБ | cБ | B | -2 | -5 | 0 | 0 | 0 |
| | | | x1 | x2 | x3 | x4 | x5 |
| x3 | 0 | 20 | 1 | 1 | 1 | 0 | 0 |
| x4 | 0 | 36 | 1 | 2 | 0 | 1 | 0 |
| x5 | 0 | 40 | 3 | 1 | 0 | 0 | 1 |
| | | 0 | 2 | 5 | 0 | 0 | 0 |
| x3 | 0 | 2 | 1/2 | 0 | 1 | -1/2 | 0 |
| x2 | -5 | 18 | 1/2 | 1 | 0 | 1/2 | 0 |
| x5 | 0 | 22 | 5/2 | 0 | 0 | -1/2 | 1 |
| | | -90 | -1/2 | 0 | 0 | -5/2 | 0 |
Оптимальный план: x1*=0; x2*=18; x3*=2; x4*=0; x5*=22 F*=90