Файл: Теория оптимизации.docx

Математическая модель для решения данной задачи:

^F=7x1^+3x2^+6x3^+12x4^{max; 3x}1^+x2^+2x3^+4x4 <sup>440;

x</sup>1^+8x2^+6x3^+2x4 ^{200; x}1^+4x2^+7x3^+2x4 <sup>320;


x</sup>j ^{0, j=1,4 .}

Форма для ввода условий данной задачи может иметь следующий вид:


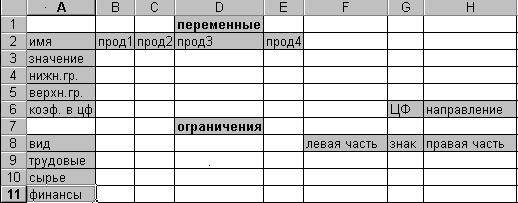
Рис. 1

Весь текст на рис.1 (и в дальнейшем) является комментарием и на решение задачи не влияет.

Далее необходимо ввести в сформированную форму исходные данные (коэффициенты в целевой функции и ограничениях, а также направление оптимизации целевой функции и знаки ограничений (рис.2)


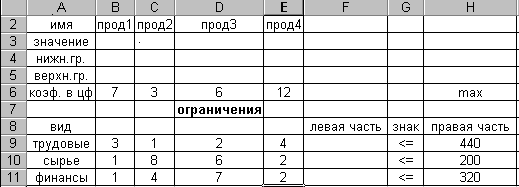
Рис.2

При этом ячейки B3:E3 являются изменяемыми и в них будут заноситься значения переменных.

Ввод функциональных зависимостей для целевой функции и ограничений осуществляется с использованием Мастера'>Мастера функций. Для этого необходимо активизировать требуемую ячейку (F6) и вызвать Мастер функций. В левой

---

части появившегося диалогового окна нужно выбрать категорию функции Математическая,а в правом окне выделить функцию СУММПРОИЗВ и нажать клавишу ОК. Затем на экране отобразится диалоговое окно второго шага (рис.8), где требуется ввести как первый (B$3:E$3), так и второй массивы (B6:E6). При вводе первого массива используются абсолютные ссылки на ячейки, при вводе второго - относительные, что в дальнейшем будет удобно при копировании формул. Во все окна адреса ячеек удобно вводить не с клавиатуры, а протаскивая мышь по соответствующим ячейкам.


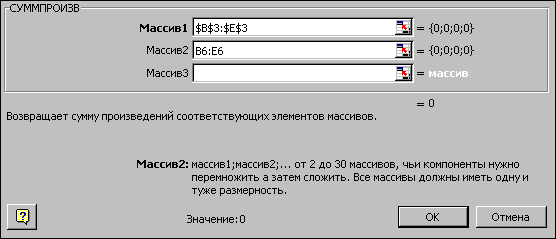
Рис.3
Зависимости для левых частей ограничений вводятся аналогично. При этом необходимо лишь менять адреса ячеек. Для ускорения и удобства ввода можно скопировать содержимое ячейки F6 в ячейки F9, F10 и F11 (при этом все относительные ссылки изменятся автоматически).

Окончательная таблица с исходными данными представлена на рис.4.

---

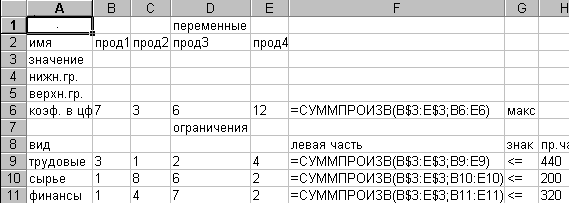
Рис. 4

После окончания ввода исходных данных осуществляется вызов программы Поиск решения.Для этого необходимо выбрать в меню пункт Данные, а в нем – Поиск решения, в результате чего на экране появится окно поиска решения (рис.5).


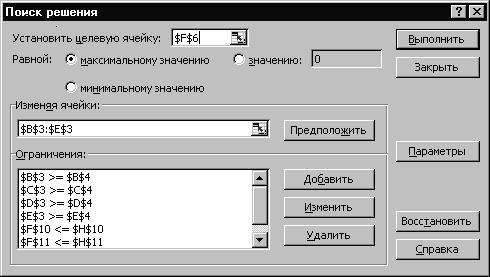
Рис.5

В окне Установить целевую ячейку требуется ввести имя ячейки, в которую введена зависимость для целевой функции (в данном случае F6). В качестве направления оптимизации выбирается максимизация. В окне Изменяя ячейки вводятся адреса ячеек, соответствующих варьируемым переменным задачи ($B3:$E3). Далее необходимо ввести ограничения. Для добавления ограничений выбирается пункт Добавить, после чего появляется окно добавления ограничений (рис.6)



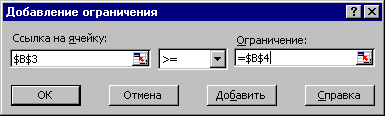
Рис.6
Вводятся граничные условия для переменных (Прод1 - Прод4) 0:

$B3>= $B4, $C3 >= $C4, $D3 >= $D4, $E3 >= $E4 (нулевые значения ячеек

---

B4-E4

можно не устанавливать). Ограничения можно также ввести в виде $B3 >= 0, $C3

>= 0, $D3 >= 0, $E3 >= 0. Затем вводятся ограничения на ресурсы: $F9 <=

$H9, $F10 <= $H10, $F11 <= $H11. Ограничения вводят последовательно. Сначала выбирается пункт Добавить, далее в появившихся диалоговых окнах вводится левая часть, знак и правая часть каждого ограничения. После ввода последнего ограничения и нажатия OK произойдет возврат в окно Поиск решения.

Решение задачи производится сразу же после ввода данных, когда на экране находится диалоговое окно Поиск решения. Перед началом решения необходимо установить параметры решения, для чего в окне поиска решения выбрать команду параметры. Диалоговое окно параметров поиска решения представлено на рис. 7.



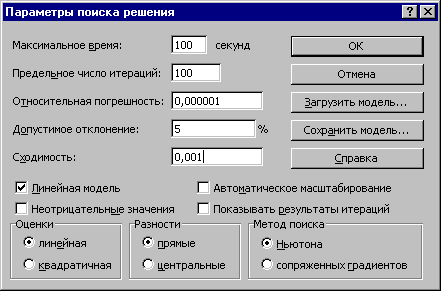
Рис.7
С помощью команд, находящихся в этом диалоговом окне, можно вводить условия для решения задач оптимизации всех

---

классов. Рассмотрим наиболее важные команды, применяемые при решении конкретных задач.

---