Файл: Отчет по лабораторной работе 2 по дисциплине Механика жидкости и газа.docx
Добавлен: 04.12.2023
Просмотров: 217
Скачиваний: 9
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Отчет по лабораторной работе №2 по дисциплине«Механика жидкости и газа»
1 КРАТКАЯ ТЕОРИЯ ИЗМЕРЕНИЯ СКОРОСТИ
2 ОПИСАНИЕ ЛАБОРАТОРНОЙ УСТАНОВКИ И ИЗМЕРИТЕЛЬНОГО ОБОРУДОВАНИЯ
2.1 УСТРОЙСТВО И СХЕМА АЭРОДИНАМИЧЕСКОЙ ТРУБЫ
3 ФИЗИЧЕСКАЯ МОДЕЛЬ ИЗМЕНЕНИЯ ИЗМЕРЯЕМОГО ДАВЛЕНИЯ
5 ПОРЯДОК ПРОВЕДЕНИЯ ЭКСПЕРИМЕНТА
6.2 РЕЗУЛЬТАТЫ ПЕРВИЧНОЙ СТАТИСТИЧЕСКОЙ ОБРАБОТКИ ИЗМЕРЕНИЙ
6.3 ОСРЕДНЕНИЕ РЕЗУЛЬТАТОВ РАСЧЕТА СКОРОСТИ И ДАВЛЕНИЙ
7 РЕЗУЛЬТАТЫ ИЗМЕРЕНИЯ И ТЕОРЕТИЧЕСКОГО РАСЧЁТА
Б.1. Измеренные перепады давлений и измеренные давления
Б.2. Ошибка измерения атмосферных давления и температуры
Б.3. Ошибка определения плотности воздуха
2 ОПИСАНИЕ ЛАБОРАТОРНОЙ УСТАНОВКИ И ИЗМЕРИТЕЛЬНОГО ОБОРУДОВАНИЯ
2.1 УСТРОЙСТВО И СХЕМА АЭРОДИНАМИЧЕСКОЙ ТРУБЫ
Лабораторная установка представляет собой аэродинамическую трубу (рисунок 1) с сужающимся соплом 8. Невозмущенный поток воздуха засасывается в корпус 5 аэродинамической трубы и затем разгоняется вентилятором 1, который вращается электродвигателем 2. Для разрубания вихрей и уменьшения их в масштабе после вентилятора расположен турбулизатор 9, а для выравнивания потока после спрямляющая решетка 6. Далее расположено сужающееся сопло 8, необходимое для ускорения дозвукового потока. Само сопло препарировано в двух сечениях для измерения статического давления.
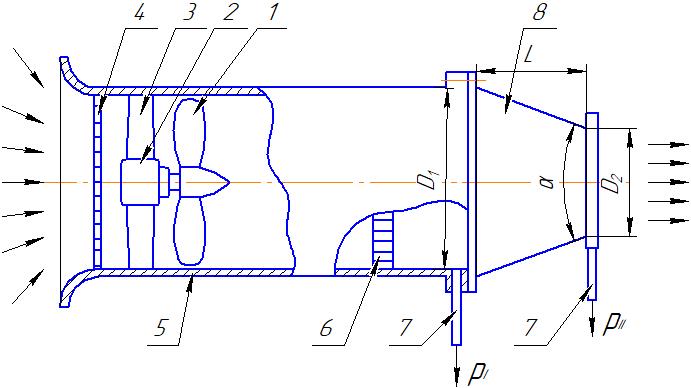
Рисунок 1 – Схема аэродинамической трубы: 1 – вентилятор; 2 – электродвигатель;
3 – направляющая решетка 4 – защитная сетка; 5 – корпус; 6 – выпрямляющая решетка;
7 – приемник статического давления; 8 – сопло I-й секции; 9 – турбулизатор
2.2 СХЕМА ПРЕПАРИРОВАНИЯ
Скорость воздушного потока на выходе из аэродинамической трубы можно измерить двумя косвенными способами: произвести замер давления с помощью трубки Пито и по перепаду статических давлений, после чего найти скорость исходя из уравнения Бернулли.
При первом способе измерения перепад статических давлений ∆p принимается с помощью приемников 7 (рисунок 1), расположенных в характерных сечениях трубы. В каждом из этих сечений расположено 4 приемника, объединенных общим коллектором, давление в котором усредняется по сечению. Перепад давлений в двух коллекторах (I, II) измеряется водяным манометром (рисунок 2).
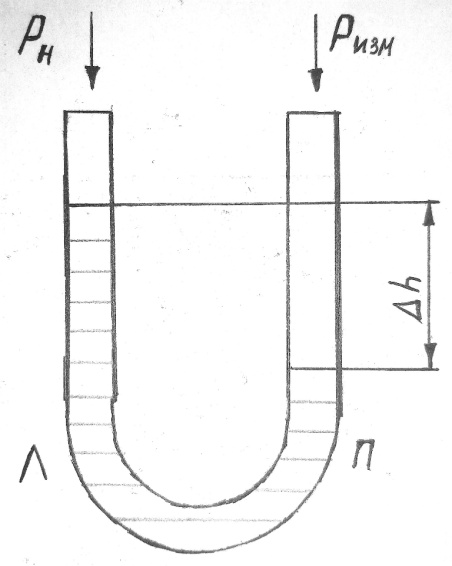
Рисунок 2 – Схема водяного манометра
3 ФИЗИЧЕСКАЯ МОДЕЛЬ ИЗМЕНЕНИЯ ИЗМЕРЯЕМОГО ДАВЛЕНИЯ
В общем случае, воздух, попадая в аэродинамическую трубу, начинает разгоняться вентилятором, который вращается электродвигателем. После чего воздух, проходя через сечение 1-1 (рисунок 3), начинает сжиматься и (исходя из уравнения Бернулли)
ускоряться до тех пор, пока не пройдет сечение 2-2.
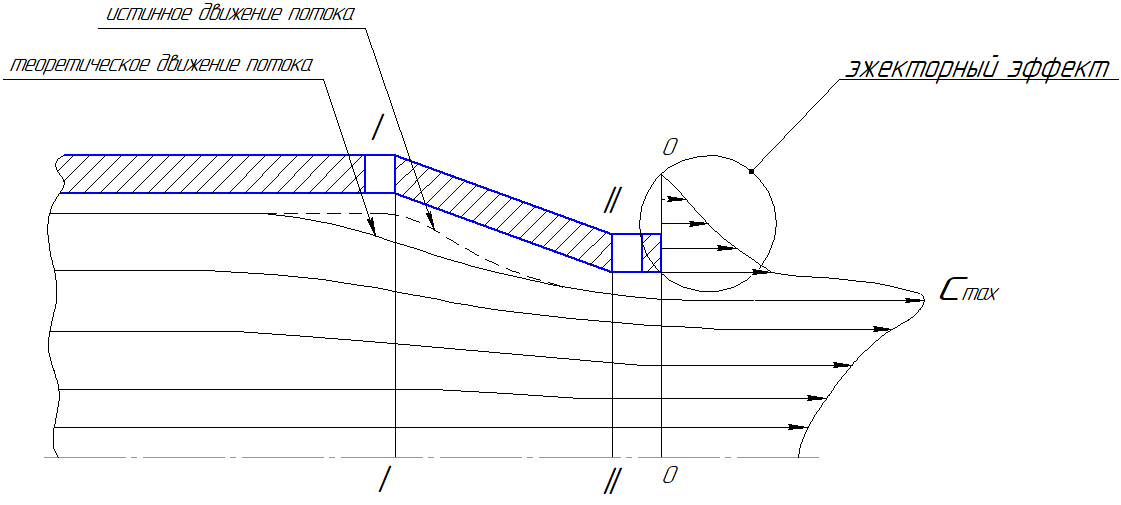
Рисунок 3 – Схема движения потока воздуха в аэродинамической трубе
При более подробном рассмотрении процесса течения потока воздуха будет понятно, что струйки воздуха, находящиеся в непосредственной близости от стенок канала, до сечения 1-1 расширяются, а затем начинают сжиматься. Струйки воздуха, расположенные ближе к центру трубы, будут постоянно сжиматься и ускоряться.
Из-за небольшого расширения пристенных струек потока воздуха возможны небольшие потери в кинетической энергии потока, но вследствие их незначительности, ими можно пренебречь.
Также на выходе из аэродинамической трубы будет наблюдаться эжекторный эффект (рисунок 4) – после выходного сечения будет подсасываться воздух из окружающей среды. Такой эффект приведет к тому, что скорость вне аэродинамической трубы после сечения 0-0 будет не нулевая.
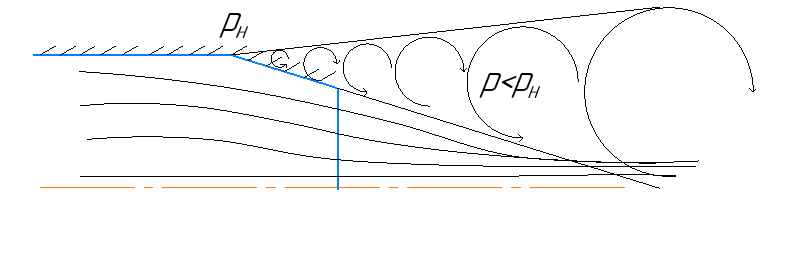
Рисунок 4 – Образование подсасывания (эжекторного эффекта)
4 МАТЕМАТИЧЕСКАЯ МОДЕЛЬ
В лабораторной работе принимается, что течение установившееся и жидкость несжимаемая (
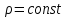 ), поэтому для получения формулы нахождения скорости необходимо использовать уравнение неразрывности:
), поэтому для получения формулы нахождения скорости необходимо использовать уравнение неразрывности: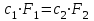 (11)
(11)Способ измерения скорости воздушного потока – по перепаду давлений основан на использовании уравнения Бернулли. Скорости с1 и с2 потока в двух произвольных сечениях трубы 1 и 2 связаны со статическими давлениями P1 и P2 в этих сечениях:
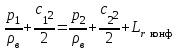 , (12)
, (12)где
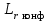 - работа гидросопротивлений равна:
- работа гидросопротивлений равна: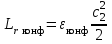 (13)
(13)Коэффициент влияния сопротивления конфузора
 рассчитывается по формуле:
рассчитывается по формуле: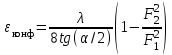 , (14)
, (14)где
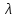 - коэффициент гидравлического трения в гидравлике.
- коэффициент гидравлического трения в гидравлике.5 ПОРЯДОК ПРОВЕДЕНИЯ ЭКСПЕРИМЕНТА
1. Проверить схему подключения трубки Пито для раздельного измерения давлений.
2. Проверить отсутствие посторонних предметов в рабочей зоне аэродинамической трубы. Визуальным осмотром убедиться в отсутствии повреждений и неисправностей трубы и приёмников давления.
3. Записать в протокол измерений дату измерения и показания барометра-анероида (атмосферные давление и температура).
4. Подключить приемники статического давления 7 (рисунок 1) к двум водяным манометрам (рисунок 2). Один из концов каждого водяного манометра сообщается с окружающей средой.
5. Включить электропитание установки и запустить аэродинамическую трубу.
6. Выждать несколько минут для установления потоков в рабочем помещении.
7. После выхода аэродинамической трубы на установившийся режим работы произвести замеры высот левого и правого столбцов жидкости (hлев и hправ) на двух манометрах. Один манометр измеряет статическое давление на входе (в широком сечении), другой – на выходе (в узком сечении).
8. Выключить установку и отключить установку от сети.
6 РЕЗУЛЬТАТЫ ПРЯМЫХ ИЗМЕРЕНИЙ
6.1 ОСНОВНЫЕ ДАННЫЕ
Измерения осуществлены:
– дата измерения – 30.04.20;
– атмосферное давление B = 752,2 мм рт.ст;
– атмосферная температура t = 17,5 °C.
Прямые измерения уровней жидкости в левом и правом коленах U‑образных дифференциальных манометров приведены в приложении А.
6.2 РЕЗУЛЬТАТЫ ПЕРВИЧНОЙ СТАТИСТИЧЕСКОЙ ОБРАБОТКИ ИЗМЕРЕНИЙ
Так как исследуется дозвуковой поток при малых числах М, то работа гидросопротивлений будет очень мала по сравнению с основным давлением, а это значит, что ее можно не учитывать при выводе формулы.В связи с чем, уравнение Бернулли (12) примет вид:
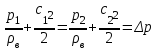 . (15)
. (15)В формуле (15) ∆p – искомая разность статических давлений.
Учитывая несжимаемость воздуха при малых скоростях, формула (11)
из соотношения (15) получится:
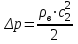 . (16)
. (16)При этом скорость будет определяться следующим выражением:
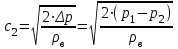 . (17)
. (17)В лабораторной практике большинство измерений – косвенные и интересующая величина является функцией одной или нескольких непосредственно измеряемых величин. Как следует из теории вероятностей, среднее значение величины с использованием средних значений непосредственно измеряемых величин.
Требуется найти абсолютную и относительную ошибки этой функции, если известны ошибки независимых переменных. Учитываются систематические и случайные ошибки.
Первым делом следует определить давление невозмущённого потока, то есть атмосферное:
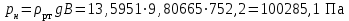 . (18)
. (18)Формулы для получения статического и полного давления можно получить из уравнения Бернулли (15):
Из равенства можно выразить расчётную формулу, учитывая, что
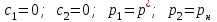 :
: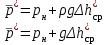 , (19)
, (19)где
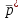 - среднее значение измеренного полного давления,
- среднее значение измеренного полного давления, 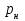 - атмосферное давление,
- атмосферное давление, 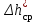 - среднее значение изменения высоты уровня жидкости, предполагается равенство плотности воды 1 г/см3.
- среднее значение изменения высоты уровня жидкости, предполагается равенство плотности воды 1 г/см3.Для статического аналогично:
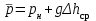 ; (20)
; (20)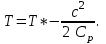
6.3 ОСРЕДНЕНИЕ РЕЗУЛЬТАТОВ РАСЧЕТА СКОРОСТИ И ДАВЛЕНИЙ
Обычно в лабораторных условиях измеряют три параметра: полное давление р*, статическое давление р и температуру торможения Т*. Поэтому эти переменные являются независимыми, все остальные параметры потока являются зависимыми. Для нахождения остальных параметров необходимо использовать дополнительные связи в виде расчетных формул:
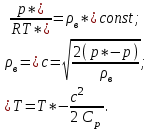 (21)
(21)Так как в ходе лабораторной работы получены неравномерные распределения давлений и температур, их необходимо осреднить. Но так как температура меняется на малые доли градусов, то её можно считать постоянной по поперечному сечению струи и в атмосфере, и не осреднять.
Таким образом, необходимо осреднить три величины: полное давление, статическое давление и скорость. Для этого нужно использовать законы сохранения.
Для осреднения давления используется закон сохранения полного импульса: