Файл: Отчет по лабораторной работе 2 по дисциплине Механика жидкости и газа.docx

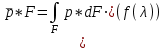, (22)

где 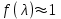- газодинамическая функция, которая при 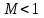примерно равна 1, поэтому осреднение по импульсу сводится к осреднению по площади.

Тогда формула (19) для осреднения полного давления будет выглядеть следующим образом:

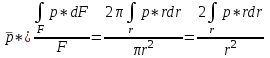(23)

Аналогично получается и для статического давления:

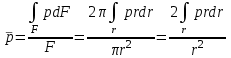. (24)

Скорость потока необходимо осреднить с помощью трех законов сохранения: закон сохранения секундного количества движения (25), закон сохранения вещества (26) и закон сохранения кинетической энергии (27), соответственно:

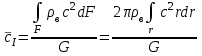; (25)

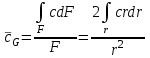; (26)

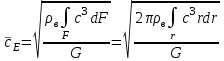; (27)

Расход рассчитывается по формуле:

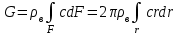. (28)

При этом интегрирование числителя дробей производится по формуле Симпсона:

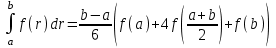. (29)

При осреднении скорости по закону сохранения вещества необходимо вычислить массовый расход путём интегрирования распределения скорости. Расход также вычисляется для двух струй: истекающей из сопла аэродинамической трубы G_тр и полной струи G_с.

---

7 РЕЗУЛЬТАТЫ ИЗМЕРЕНИЯ И ТЕОРЕТИЧЕСКОГО РАСЧЁТА

В данной лабораторной работе замеры проводились для полной струи. Но расчеты необходимо произвести для двух струй: вытекающей только из сопла (радиус от 0 до 124 мм) и полной струи (от радиуса 0 до 140 мм), для того чтобы увидеть как влияет внешний эжектированный поток на измеряемые параметры.

1. 
   Расчеты полного, статического давления и температуры приведены в приложении А в таблице А.3.
   
2. 
   Расчет осредненного полного и статического давления до r=140 мм:
   

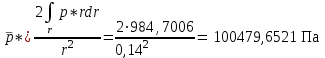; (30)

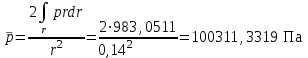. (31)

Осреднение до r=124 мм:

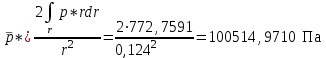; (32)

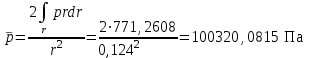. (33)

3. 
   Расчеты скорости приведены в приложении А в таблице А.3
   
4. 
   Расчет расхода для полной струи до r=140 мм:
   

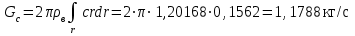. (34)

Для струи, истекающей из сопла аэродинамической трубы r=124 мм:

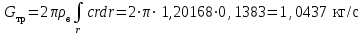. (35)

Расход эжектированного атмосферного воздуха находится по формуле:

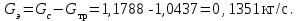(36)

5. 
   Расчет осредненных скоростей до r=140 мм:
   

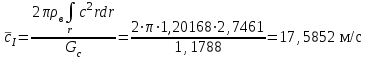, (37)

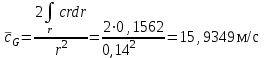, (38)

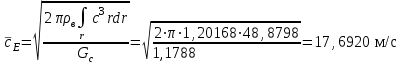. (39)

Осреднение до r=124 мм:

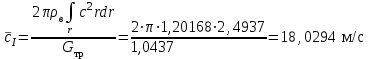, (40)

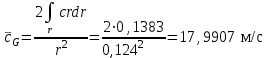, (41)

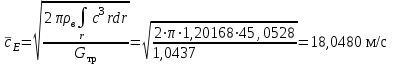. (42)

8 АНАЛИЗ РЕЗУЛЬТАТОВ

Результаты в виде построенных таблиц и экспериментальных теоретических графиков с «коридорами» ошибок получены и их можно увидеть в приложении А.

Судя по полученным результатам, экспериментальные графики лежат практически ниже теоретических, что обусловлено погрешностями измерения.

Также из Приложения А можно заметить, что для

---

происходит смена знака. Так как поток подсасывает с верхней кромки сопла, то есть происходит эжекция, то там возникает зона разряжения, следовательно, давление меньше атмосферного, это видно из расчетов по таблице А.3. Поэтому 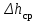принимает знак минус. Эжектированный расход был посчитан в формуле (36), он равен: 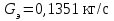, что составляет 12,94% от расхода истекающей из сопла трубы струи.

Также видно, что температура по всему сечению сопла почти не меняется, так как при малых мощностях трубы тепла подводится совсем мало.

На полученных графиках в приложении А видно, что для струи, вытекающей из сопла, вертикальные линии осредненных скоростей: 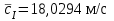, , 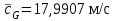, 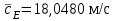лежат между минимальной скоростью на оси канала равной 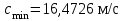и максимальной скоростью, которая находится внутри струи вблизи стенки сопла и равна 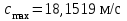. Это значит, что осреднение адекватно.

Для осредненных значений давлений прослеживается аналогичная ситуация. Осредненные значения полного и статического давления соответственно равны: , .

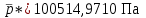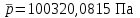Сравнивая значения осредненных скоростей для полной струи и струи из сопла (таблица 1) видно, что потери в пограничном слое оказывают не большое влияние на средние величины.

Таблица 1.

	Полная струя	Струя из сопла
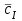, м/с	17,5852	18,0294
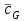, м/с	15,9349	17,9907
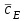, м/с	17,6920	18,0480
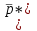, Па	100479,6521	100514,9710
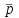, Па	100311,3319	100320,0815

---

---

ЗАКЛЮЧЕНИЕ

1. 
   Получен практический опыт и произведены замеры скоростей по перепаду статических давлений. Для статистики и получения более точного результата замеры производились 8 раз.
   

6. 
   Данный способ подходит для быстрого замера средней скорости по сечению аэродинамической трубы и не позволяет измерять скорость потока в центре сечения.
   
7. 
   При движении потока в сужающемся канале скорость струек уменьшается по мере приближения к центру сопла из-за того, что возмущения, которые образовались вблизи стенок не успевают дойти до центра
   
8. 
   Осредненные параметры удовлетворяют измеренным величинам, так как каждый из параметров лежит в пределах от минимального значения до максимального.
   

Для струи из сопла = 17,9907 м/с;

r = 120мм

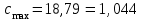
r = 20мм

9. 
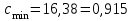
   Средняя ошибка измерения давления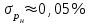 меньше 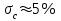на два порядка. Это можно объяснить тем, что исходя из уравнения Бернулли, при малых значениях скорости (М<0,05) малое изменение давления влечет за собой сильное изменение скорости.
   
10. 
    Явление подсасывания в полной струе порождает турбулентный поток, вызывающий увеличение ошибок измерений параметров:
    

r = 124мм

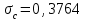
r = 126мм

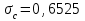
За кромкой сопла средняя ошибка увеличилась на 42% относительно ошибки перед кромкой сопла.

11. 
    Параметры осредненные по полной струе ниже,
    чем осредненные по струе из сопла:
    

упала на 1,97%

упала на 2,46%

упала на 11,42%

12. 
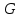    Сильное падение объясняется тем, что растет пропорционально квадрату радиуса. Исходя из расчетов, 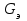составил 13% от полного расхода ( 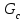). Это объясняет падение на 11,42%.
    
13. 
    Исходя из расчетов осредненной скорости, получается неравенство:
    

---