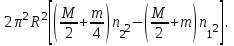Файл: Учебнометодическое пособие по дисциплине физика часть 1 Физические основы механики. Электричество. Электромагнетизм. Для студентов 1 курса.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.12.2023
Просмотров: 532
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, поэтому кинетическая энергия тел после соударения стала меньше на величину
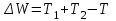 ,
,
где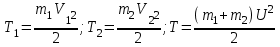
Итак,
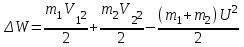 (4)
(4)
П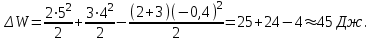
одставляя числовые значения в формулу (4) в первом случае получим
Во втором случае будем иметь
П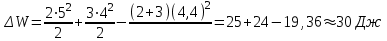
р и м е р 6. Через блок в виде сплошного диска, имеющего массу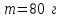 (рис.3) перекинута тонкая гибкая нить, к концам которой подвешены грузы массами m1=100г и m2=200г. С каким ускорением будут двигаться грузы, если их предоставить самим себе? Трением и массой нити пренебречь.
(рис.3) перекинута тонкая гибкая нить, к концам которой подвешены грузы массами m1=100г и m2=200г. С каким ускорением будут двигаться грузы, если их предоставить самим себе? Трением и массой нити пренебречь.
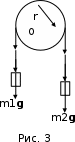
Д
T1׳
T2׳
ано: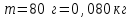 ;
;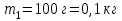 ;
; 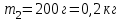 .
.
Найти: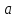 .
.
Р
X
T1
T2
е ш е н и е .Воспользуемся основными уравнениями динамики поступательного и вращательного движений. Для этого рассмотрим силы, действующие на каждый груз в отдельности и на блок. На первый груз действует две силы: сила тяжести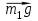 ; и сила упругости (сила натяжения нити)
; и сила упругости (сила натяжения нити)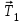 .Спроектируем эти силы на ось X, которую направим вертикально вниз, напишем уравнение движения (второй закон Ньютона) в координатной форме:
.Спроектируем эти силы на ось X, которую направим вертикально вниз, напишем уравнение движения (второй закон Ньютона) в координатной форме:
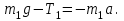 (1)
(1)
Уравнение движения для второго груза запишется аналогично
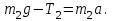 (2)
(2)
Под действием двух моментов сил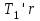 и
и 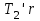 относительно оси О, перпендикулярной плоскости чертежа, блок приобретает угловое ускорение
относительно оси О, перпендикулярной плоскости чертежа, блок приобретает угловое ускорение
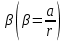 . Согласно основному уравнению динамики вращательного движения
. Согласно основному уравнению динамики вращательного движения
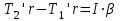 (3)
(3)
Где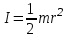 - момент инерции блока (сплошного диска) относительно оси О.
- момент инерции блока (сплошного диска) относительно оси О.
Сила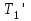 согласно третьему закону Ньютона по абсолютной величине равна силе
согласно третьему закону Ньютона по абсолютной величине равна силе 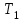 . Соответственно сила
. Соответственно сила 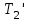 по абсолютной величине равна силе
по абсолютной величине равна силе 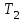 . Воспользовавшись этим, подставим в уравнение (3) вместо
. Воспользовавшись этим, подставим в уравнение (3) вместо 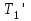 и
и 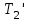 , выражения для
, выражения для 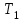 и
и 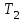 , получив их предварительно из уравнений (1)и (2):
, получив их предварительно из уравнений (1)и (2):
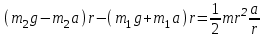
После сокращения на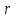 и перегруппировки членов найдём искомое ускорение
и перегруппировки членов найдём искомое ускорение
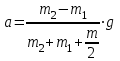 .(4)
.(4)
Отношение масс в правой части формулы (4) есть величина безразмерная. Поэтому числовые значения масс ,
,  и
и 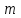 можно выразить в граммах, как они даны в условии задачи. Числовые значения ускорения
можно выразить в граммах, как они даны в условии задачи. Числовые значения ускорения 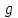 надо взять в единицах СИ. После подстановки получим
надо взять в единицах СИ. После подстановки получим
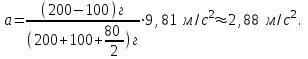
П р и м е р 7. Маховик в виде сплошного диска радиусом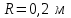 и массой
и массой 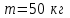 раскручен до частоты вращения
раскручен до частоты вращения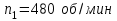 и предоставлен самому себе. Под действием сил трения маховик остановился через
и предоставлен самому себе. Под действием сил трения маховик остановился через 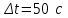
. Найти момент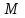 сил трения.
сил трения.
Дано: ;
;  ;
; 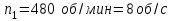 ;
; 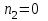 ;
;  .
.
Найти: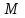 .
.
Р е ш е н и е .Для решения задачи воспользуемся основным уравнением динамики вращательного движения в виде
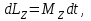 (1)
(1)
где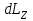 – изменение момента импульса маховика, вращающегося относительно оси Z, совпадающей с геометрической осью маховика, за интервал времени
– изменение момента импульса маховика, вращающегося относительно оси Z, совпадающей с геометрической осью маховика, за интервал времени  ;
;
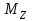 -момент внешних сил (в нашем случае момент сил трения), действующих на маховик относительно той же оси.
-момент внешних сил (в нашем случае момент сил трения), действующих на маховик относительно той же оси.
Момент сил трения можно считать не изменяющимся с течением времени (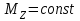 ), поэтому интегрирование уравнения (1) приводит к выражению
), поэтому интегрирование уравнения (1) приводит к выражению
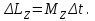 (2)
(2)
При вращении твердого тела относительно неподвижной оси изменение момента импульса
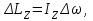 (3)
(3)
где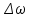 – изменение угловой скорости маховика;
– изменение угловой скорости маховика;
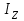 – момент инерции маховика относительно оси Z.
– момент инерции маховика относительно оси Z.
Приравняв правые части равенства (2) и (3), получим
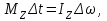
Откуда
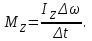 (4)
(4)
Момент инерции маховика в виде сплошного диска определяется по формуле
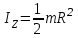
Изменение угловой скорости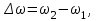 выразим через конечную
выразим через конечную
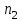 и
и  начальную n1 частоты вращения, пользуясь соотношением
начальную n1 частоты вращения, пользуясь соотношением 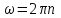
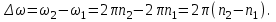
Подставив в формулу (4) найденные выражения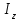 и
и  , получим
, получим
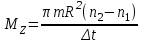 .(5)
.(5)
Выполним проверку размерности результата:
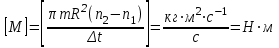
Подставляя числовые значения в формулу (5), получим:
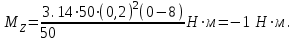
Знак минус показывает, что силы трения оказывают на маховик тормозящее действие.
П р и м е р 8. Горизонтальная платформа в виде диска массой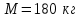 и радиусом
и радиусом 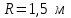 вращается с частотой
вращается с частотой 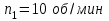 около вертикальной оси без трения.
около вертикальной оси без трения.
На краю платформы стоит человек, масса которого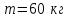 . С какой частотой
. С какой частотой 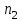 будет вращаться платформа, если человек перейдёт в точку платформы, находящуюся на расстоянии
будет вращаться платформа, если человек перейдёт в точку платформы, находящуюся на расстоянии 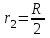 от центра платформы? Момент инерции человека рассчитать как для материальной точки. Какую работу совершит человек при этом переходе?
от центра платформы? Момент инерции человека рассчитать как для материальной точки. Какую работу совершит человек при этом переходе?
Дано: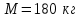 ;
; 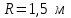 ;
; 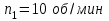 ;
; 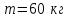 ;
; 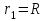 ;
; 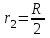 .
.
Найти: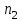 ;
; 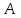 .
.
Р е ш е н и е .Так как силы тяжести платформы и человека параллельны вертикальной оси, то момент внешних сил относительно этой оси вращения Z, совпадающей с геометрической осью платформы, равен нулю.
При этом условии момент импульса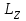 системы платформа-человек остаётся постоянным
системы платформа-человек остаётся постоянным
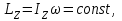 (1)
(1)
где – момент инерции платформы с человеком относительно оси Z,
– момент инерции платформы с человеком относительно оси Z,
 –угловая скорость платформы.
–угловая скорость платформы.
Момент инерции системы равен сумме моментов инерции тел, входящих в состав системы, поэтому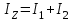 , где
, где 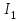 - момент инерции платформы;
- момент инерции платформы; 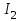 - момент инерции человека.
- момент инерции человека.
С учетом этого равенство (1) примет вид
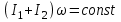
или
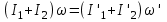 (2)
(2)
Здесь нештрихованные значения величин относятся к начальному состоянию, штрихованные - к конечному состоянию.
Момент инерции платформы (сплошного диска) относительно оси Z при переходе человека не изменяется:
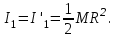
Момент инерции человека относительно той же оси будет изменяться. Если рассчитывать момент инерции человека как для материальной точки, то
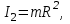 а
а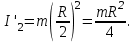
Подставим в формулу (2) найденные выражения моментов инерции, а также выразим угловые скорости через частоту вращения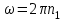 и
и 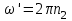 :
:
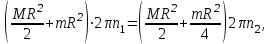
откуда
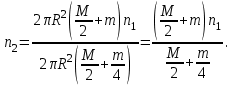 (3)
(3)
После подстановки числовых значений получим
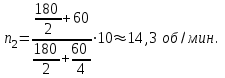
Работу, совершаемую человеком при переходе, найдем как изменение кинетической энергии системы платформа–человек:
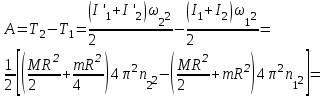
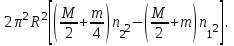
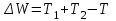 ,
,где
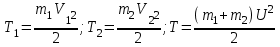
Итак,
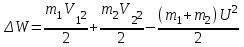 (4)
(4)П
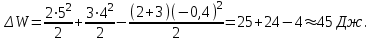
одставляя числовые значения в формулу (4) в первом случае получим
Во втором случае будем иметь
П
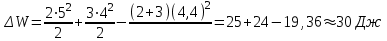
р и м е р 6. Через блок в виде сплошного диска, имеющего массу
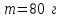 (рис.3) перекинута тонкая гибкая нить, к концам которой подвешены грузы массами m1=100г и m2=200г. С каким ускорением будут двигаться грузы, если их предоставить самим себе? Трением и массой нити пренебречь.
(рис.3) перекинута тонкая гибкая нить, к концам которой подвешены грузы массами m1=100г и m2=200г. С каким ускорением будут двигаться грузы, если их предоставить самим себе? Трением и массой нити пренебречь.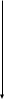
Д
T1׳
T2׳
ано:
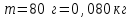 ;
;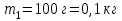 ;
; 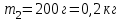 .
.Найти:
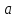 .
.Р
X
T1
T2
е ш е н и е .Воспользуемся основными уравнениями динамики поступательного и вращательного движений. Для этого рассмотрим силы, действующие на каждый груз в отдельности и на блок. На первый груз действует две силы: сила тяжести
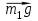 ; и сила упругости (сила натяжения нити)
; и сила упругости (сила натяжения нити)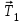 .Спроектируем эти силы на ось X, которую направим вертикально вниз, напишем уравнение движения (второй закон Ньютона) в координатной форме:
.Спроектируем эти силы на ось X, которую направим вертикально вниз, напишем уравнение движения (второй закон Ньютона) в координатной форме: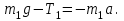 (1)
(1)Уравнение движения для второго груза запишется аналогично
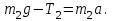 (2)
(2)Под действием двух моментов сил
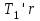 и
и 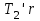 относительно оси О, перпендикулярной плоскости чертежа, блок приобретает угловое ускорение
относительно оси О, перпендикулярной плоскости чертежа, блок приобретает угловое ускорение
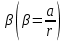 . Согласно основному уравнению динамики вращательного движения
. Согласно основному уравнению динамики вращательного движения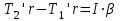 (3)
(3)Где
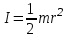 - момент инерции блока (сплошного диска) относительно оси О.
- момент инерции блока (сплошного диска) относительно оси О. Сила
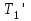 согласно третьему закону Ньютона по абсолютной величине равна силе
согласно третьему закону Ньютона по абсолютной величине равна силе 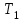 . Соответственно сила
. Соответственно сила 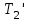 по абсолютной величине равна силе
по абсолютной величине равна силе 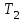 . Воспользовавшись этим, подставим в уравнение (3) вместо
. Воспользовавшись этим, подставим в уравнение (3) вместо 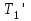 и
и 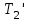 , выражения для
, выражения для 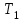 и
и 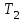 , получив их предварительно из уравнений (1)и (2):
, получив их предварительно из уравнений (1)и (2):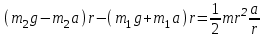
После сокращения на
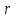 и перегруппировки членов найдём искомое ускорение
и перегруппировки членов найдём искомое ускорение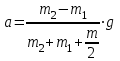 .(4)
.(4)Отношение масс в правой части формулы (4) есть величина безразмерная. Поэтому числовые значения масс
 ,
,  и
и 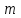 можно выразить в граммах, как они даны в условии задачи. Числовые значения ускорения
можно выразить в граммах, как они даны в условии задачи. Числовые значения ускорения  надо взять в единицах СИ. После подстановки получим
надо взять в единицах СИ. После подстановки получим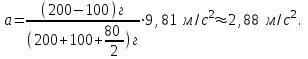
П р и м е р 7. Маховик в виде сплошного диска радиусом
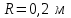 и массой
и массой 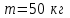 раскручен до частоты вращения
раскручен до частоты вращения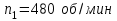 и предоставлен самому себе. Под действием сил трения маховик остановился через
и предоставлен самому себе. Под действием сил трения маховик остановился через 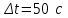
. Найти момент
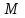 сил трения.
сил трения.Дано:
 ;
;  ;
; 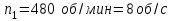 ;
; 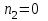 ;
;  .
.Найти:
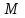 .
.Р е ш е н и е .Для решения задачи воспользуемся основным уравнением динамики вращательного движения в виде
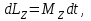 (1)
(1)где
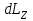 – изменение момента импульса маховика, вращающегося относительно оси Z, совпадающей с геометрической осью маховика, за интервал времени
– изменение момента импульса маховика, вращающегося относительно оси Z, совпадающей с геометрической осью маховика, за интервал времени  ;
;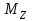 -момент внешних сил (в нашем случае момент сил трения), действующих на маховик относительно той же оси.
-момент внешних сил (в нашем случае момент сил трения), действующих на маховик относительно той же оси.Момент сил трения можно считать не изменяющимся с течением времени (
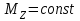 ), поэтому интегрирование уравнения (1) приводит к выражению
), поэтому интегрирование уравнения (1) приводит к выражению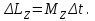 (2)
(2)При вращении твердого тела относительно неподвижной оси изменение момента импульса
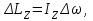 (3)
(3)где
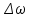 – изменение угловой скорости маховика;
– изменение угловой скорости маховика;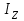 – момент инерции маховика относительно оси Z.
– момент инерции маховика относительно оси Z.Приравняв правые части равенства (2) и (3), получим
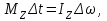
Откуда
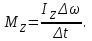 (4)
(4)Момент инерции маховика в виде сплошного диска определяется по формуле
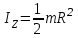
Изменение угловой скорости
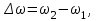 выразим через конечную
выразим через конечную
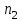 и
и  начальную n1 частоты вращения, пользуясь соотношением
начальную n1 частоты вращения, пользуясь соотношением 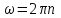
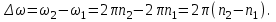
Подставив в формулу (4) найденные выражения
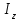 и
и  , получим
, получим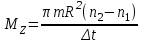 .(5)
.(5)Выполним проверку размерности результата:
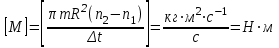
Подставляя числовые значения в формулу (5), получим:
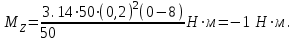
Знак минус показывает, что силы трения оказывают на маховик тормозящее действие.
П р и м е р 8. Горизонтальная платформа в виде диска массой
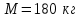 и радиусом
и радиусом 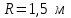 вращается с частотой
вращается с частотой 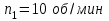 около вертикальной оси без трения.
около вертикальной оси без трения.На краю платформы стоит человек, масса которого
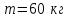 . С какой частотой
. С какой частотой 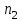 будет вращаться платформа, если человек перейдёт в точку платформы, находящуюся на расстоянии
будет вращаться платформа, если человек перейдёт в точку платформы, находящуюся на расстоянии 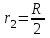 от центра платформы? Момент инерции человека рассчитать как для материальной точки. Какую работу совершит человек при этом переходе?
от центра платформы? Момент инерции человека рассчитать как для материальной точки. Какую работу совершит человек при этом переходе?Дано:
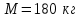 ;
; 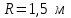 ;
; 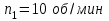 ;
; 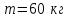 ;
; 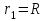 ;
; 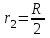 .
.Найти:
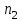 ;
; 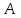 .
.Р е ш е н и е .Так как силы тяжести платформы и человека параллельны вертикальной оси, то момент внешних сил относительно этой оси вращения Z, совпадающей с геометрической осью платформы, равен нулю.
При этом условии момент импульса
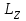 системы платформа-человек остаётся постоянным
системы платформа-человек остаётся постоянным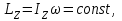 (1)
(1)где
 – момент инерции платформы с человеком относительно оси Z,
– момент инерции платформы с человеком относительно оси Z, –угловая скорость платформы.
–угловая скорость платформы.Момент инерции системы равен сумме моментов инерции тел, входящих в состав системы, поэтому
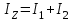 , где
, где 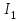 - момент инерции платформы;
- момент инерции платформы; 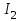 - момент инерции человека.
- момент инерции человека.С учетом этого равенство (1) примет вид
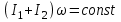
или
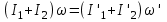 (2)
(2)Здесь нештрихованные значения величин относятся к начальному состоянию, штрихованные - к конечному состоянию.
Момент инерции платформы (сплошного диска) относительно оси Z при переходе человека не изменяется:
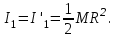
Момент инерции человека относительно той же оси будет изменяться. Если рассчитывать момент инерции человека как для материальной точки, то
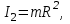 а
а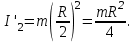
Подставим в формулу (2) найденные выражения моментов инерции, а также выразим угловые скорости через частоту вращения
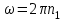 и
и 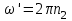 :
: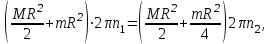
откуда
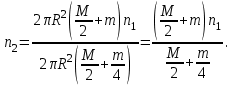 (3)
(3)После подстановки числовых значений получим
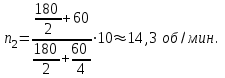
Работу, совершаемую человеком при переходе, найдем как изменение кинетической энергии системы платформа–человек: