Файл: Учебнометодическое пособие по дисциплине физика часть 1 Физические основы механики. Электричество. Электромагнетизм. Для студентов 1 курса.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.12.2023
Просмотров: 529
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
кривизны траектории движения в данный момент 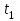 находится по значению нормальной
находится по значению нормальной  составляющей ускорения:
составляющей ускорения:
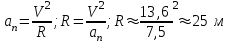
П р и м е р 3. При торможении частота вращения маховика изменилась от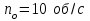 до
до 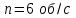
Определить угловое ускорение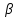 маховика и продолжительность
маховика и продолжительность 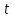 торможения, если за время равнозамедленного движения маховик сделал
торможения, если за время равнозамедленного движения маховик сделал 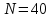 оборотов.
оборотов.
Дано: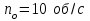 ;
; 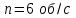 ;
; 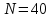 .
.
Найти: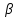 ;
; 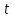 .
.
Р е ш е н и е .Угловое ускорение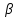 маховика связано с начальной
маховика связано с начальной 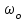 и конечной
и конечной 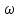 угловыми скоростями и углом поворота
угловыми скоростями и углом поворота 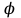 соотношением
соотношением
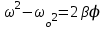 ,
,
откуда
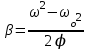
Так как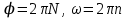 , то
, то
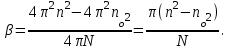 (1)
(1)
Подставляя числовые значения в выражение (1), получим
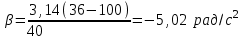 .
.
Угловое ускорение получилось отрицательным, так как маховик вращается замедленно.
Для определения продолжительности торможения используем формулу, связывающую угол поворота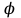 со средней угловой скоростью
со средней угловой скоростью 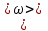 вращения маховика и временем t:
вращения маховика и временем t:
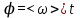
или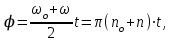
откуда
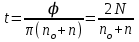 . (2)
. (2)
Подставляя числовые значения в формулу (2), получим
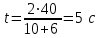 .
.
П р и м е р 4. На платформе массой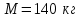 и длиной
и длиной 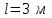 ,стоящей на рельсах, находится человек массой
,стоящей на рельсах, находится человек массой 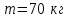 . Вначале платформа и человек неподвижны. Человек переходит с одного края платформы на другой (вдоль направления рельс). Определить, на какое расстояние сдвинется платформа. Силы сопротивления движению платформы не учитывать:
. Вначале платформа и человек неподвижны. Человек переходит с одного края платформы на другой (вдоль направления рельс). Определить, на какое расстояние сдвинется платформа. Силы сопротивления движению платформы не учитывать:
Дано: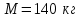 ;
; 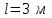 ;
; 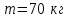 ;
; 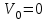 .
.
Найти: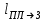
Р е ш е н и е .Система человек-платформа не является замкнутой, но в направлении вдоль рельс действует лишь сила трения, величиной которой, согласно условию задачи, можно пренебречь. Поэтому вдоль указанного направления может быть применен закон сохранения составляющей импульса в направлении рельс.
Первоначально человек и платформа неподвижны и их импульс (суммарный) равен нулю. Когда человек будет перемещаться вдоль платформы, будет перемещаться и платформа, но составляющая суммарного импульса вдоль рельс будет оставаться неизменной, равной нулю:
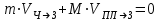 (1)
(1)
Закон сохранения импульса может быть применен лишь к инерциальной системе отсчета. Такой системой выберем Землю (или рельсы). Следовательно, здесь VЧ-Зи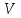 ПЛ-З – скорости человека и платформы относительно Земли.
ПЛ-З – скорости человека и платформы относительно Земли.
Умножив на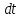 , и проинтегрировав по всему времени перемещения, получим:
, и проинтегрировав по всему времени перемещения, получим:
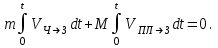
Так как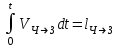
и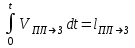 ,
,
где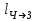 и
и  – перемещения соответственно человека и платформы относительно Земли, то
– перемещения соответственно человека и платформы относительно Земли, то
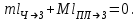 (2)
(2)
В условии задачи указана длина платформы ; человек переместился вдоль платформы на эту величину
; человек переместился вдоль платформы на эту величину 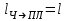 . Применяя следствие из преобразования координат Галилея, получим
. Применяя следствие из преобразования координат Галилея, получим
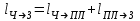 (3)
(3)
Подставив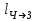 в уравнение (2), получим
в уравнение (2), получим
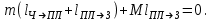
Откуда
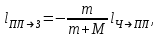
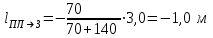
Знак минус показывает, что перемещение платформы направлено в сторону, противоположную перемещению человека.
П р и м е р 5. Два тела движутся вдоль одной прямой. Первое тело массой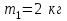 движется со скоростью
движется со скоростью 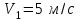 , а второе - массой
, а второе - массой 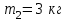 имеет скорость
имеет скорость 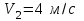 . Рассматривая тела как замкнутую систему, определить, какие скорости будут иметь тела после столкновения, если: 1)они движутся друг другу навстречу; 2) первое тело догоняет второе.
. Рассматривая тела как замкнутую систему, определить, какие скорости будут иметь тела после столкновения, если: 1)они движутся друг другу навстречу; 2) первое тело догоняет второе.
Решить задачу для двух случаев: а) тела абсолютно упругие и б) тела абсолютно неупругие. При абсолютно неупругом столкновении рассчитать потери энергии при соударении тел.
Дано: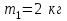 ;
;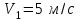 ;
;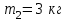 ;
;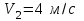 .
.
Найти: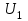 ;
; 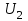
;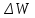 .
.
Р е ш е н и е .
А. Тела абсолютно упругие.
В случае абсолютно упругого соударения, тела при столкновении упруго деформируется. Кинетическая энергия их переходит в потенциальную энергию упруго деформированных тел. Затем эта потенциальная энергия полностью переходит в кинетическую, так как при абсолютно упругих деформациях остаточной деформации не наблюдается. Таким образом, сумма кинетических энергий тел до соударения и после него остаётся неизменной
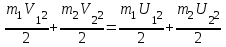 ,(1)
,(1)
Где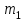 и
и 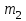 - массы тел;
- массы тел;
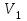 и
и 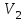 - скорости тел до соударения;
- скорости тел до соударения;
 и
и  - скорости тел после соударения.
- скорости тел после соударения.
Согласно закону сохранения импульса в замкнутой системе
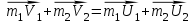 .(2)
.(2)
Так как движение происходит по одной прямой, то можно перейти от векторного уравнения (2) к алгебраическому:
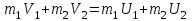 .(2/)
.(2/)
Решая систему двух уравнений (1) и (2/) относительно и
и  получим
получим
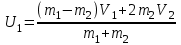 ,
,
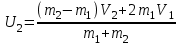 .
.
Условимся считать направление движения первого тела положительным.
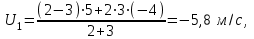
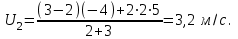
2. Если первое тело догоняет второе, т.е оба тела движутся в одну сторону, то и
и 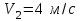 и
и
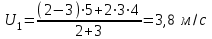 ,
,
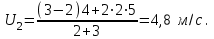
В данном случае после столкновения направление движения тел не меняется.
Б. Тела абсолютно неупругие.
При абсолютно неупругом столкновении нет упругих сил, которые заставили бы столкнувшиеся тела отталкиваться друг от друга. Поэтому после столкновения они будут двигаться вместе с одной скоростью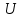 . Из закона сохранения импульса следует
. Из закона сохранения импульса следует
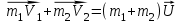 (3)
(3)
Так как движение происходит по одной прямой, то можно перейти от векторного уравнения к алгебраическому:
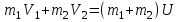 .(3/)
.(3/)
откуда
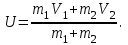
Условимся считать направление движения первого тела положительным.
Если тела движутся навстречу друг другу, т.е. в противоположные стороны, то и
и  , следовательно
, следовательно
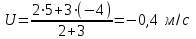
После столкновения тела движутся в ту же сторону, в которую двигалось второе тело, так как числовое значение его импульса было больше, чем у первого тела.
2.Если первое тело догоняет второе, т.е тела движутся в одну сторону, то и
и 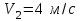 , следовательно
, следовательно
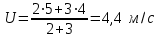
Направление движения тел остается неизменным.
3.При неупругом столкновении часть энергии переходит во внутреннюю
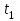 находится по значению нормальной
находится по значению нормальной  составляющей ускорения:
составляющей ускорения: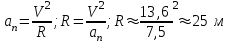
П р и м е р 3. При торможении частота вращения маховика изменилась от
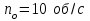 до
до 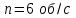
Определить угловое ускорение
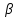 маховика и продолжительность
маховика и продолжительность 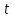 торможения, если за время равнозамедленного движения маховик сделал
торможения, если за время равнозамедленного движения маховик сделал 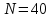 оборотов.
оборотов.Дано:
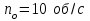 ;
; 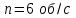 ;
; 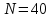 .
.Найти:
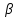 ;
; 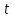 .
.Р е ш е н и е .Угловое ускорение
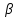 маховика связано с начальной
маховика связано с начальной 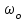 и конечной
и конечной 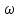 угловыми скоростями и углом поворота
угловыми скоростями и углом поворота 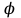 соотношением
соотношением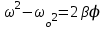 ,
,откуда
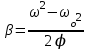
Так как
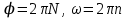 , то
, то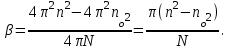 (1)
(1)Подставляя числовые значения в выражение (1), получим
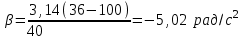 .
.Угловое ускорение получилось отрицательным, так как маховик вращается замедленно.
Для определения продолжительности торможения используем формулу, связывающую угол поворота
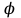 со средней угловой скоростью
со средней угловой скоростью 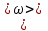 вращения маховика и временем t:
вращения маховика и временем t: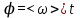
или
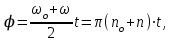
откуда
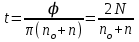 . (2)
. (2)Подставляя числовые значения в формулу (2), получим
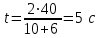 .
.П р и м е р 4. На платформе массой
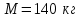 и длиной
и длиной 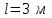 ,стоящей на рельсах, находится человек массой
,стоящей на рельсах, находится человек массой 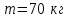 . Вначале платформа и человек неподвижны. Человек переходит с одного края платформы на другой (вдоль направления рельс). Определить, на какое расстояние сдвинется платформа. Силы сопротивления движению платформы не учитывать:
. Вначале платформа и человек неподвижны. Человек переходит с одного края платформы на другой (вдоль направления рельс). Определить, на какое расстояние сдвинется платформа. Силы сопротивления движению платформы не учитывать:Дано:
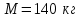 ;
; 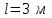 ;
; 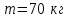 ;
; 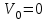 .
.Найти:
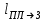
Р е ш е н и е .Система человек-платформа не является замкнутой, но в направлении вдоль рельс действует лишь сила трения, величиной которой, согласно условию задачи, можно пренебречь. Поэтому вдоль указанного направления может быть применен закон сохранения составляющей импульса в направлении рельс.
Первоначально человек и платформа неподвижны и их импульс (суммарный) равен нулю. Когда человек будет перемещаться вдоль платформы, будет перемещаться и платформа, но составляющая суммарного импульса вдоль рельс будет оставаться неизменной, равной нулю:
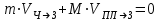 (1)
(1)Закон сохранения импульса может быть применен лишь к инерциальной системе отсчета. Такой системой выберем Землю (или рельсы). Следовательно, здесь VЧ-Зи
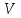 ПЛ-З – скорости человека и платформы относительно Земли.
ПЛ-З – скорости человека и платформы относительно Земли.Умножив на
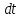 , и проинтегрировав по всему времени перемещения, получим:
, и проинтегрировав по всему времени перемещения, получим: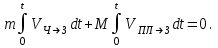
Так как
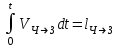
и
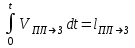 ,
,где
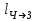 и
и  – перемещения соответственно человека и платформы относительно Земли, то
– перемещения соответственно человека и платформы относительно Земли, то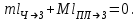 (2)
(2)В условии задачи указана длина платформы
 ; человек переместился вдоль платформы на эту величину
; человек переместился вдоль платформы на эту величину 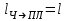 . Применяя следствие из преобразования координат Галилея, получим
. Применяя следствие из преобразования координат Галилея, получим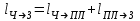 (3)
(3)Подставив
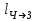 в уравнение (2), получим
в уравнение (2), получим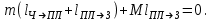
Откуда
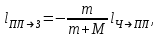
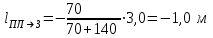
Знак минус показывает, что перемещение платформы направлено в сторону, противоположную перемещению человека.
П р и м е р 5. Два тела движутся вдоль одной прямой. Первое тело массой
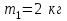 движется со скоростью
движется со скоростью 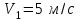 , а второе - массой
, а второе - массой 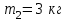 имеет скорость
имеет скорость 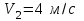 . Рассматривая тела как замкнутую систему, определить, какие скорости будут иметь тела после столкновения, если: 1)они движутся друг другу навстречу; 2) первое тело догоняет второе.
. Рассматривая тела как замкнутую систему, определить, какие скорости будут иметь тела после столкновения, если: 1)они движутся друг другу навстречу; 2) первое тело догоняет второе.Решить задачу для двух случаев: а) тела абсолютно упругие и б) тела абсолютно неупругие. При абсолютно неупругом столкновении рассчитать потери энергии при соударении тел.
Дано:
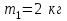 ;
;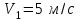 ;
;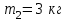 ;
;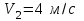 .
.Найти:
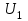 ;
; 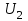
;
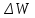 .
.Р е ш е н и е .
А. Тела абсолютно упругие.
В случае абсолютно упругого соударения, тела при столкновении упруго деформируется. Кинетическая энергия их переходит в потенциальную энергию упруго деформированных тел. Затем эта потенциальная энергия полностью переходит в кинетическую, так как при абсолютно упругих деформациях остаточной деформации не наблюдается. Таким образом, сумма кинетических энергий тел до соударения и после него остаётся неизменной
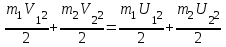 ,(1)
,(1)Где
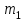 и
и 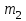 - массы тел;
- массы тел;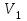 и
и 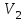 - скорости тел до соударения;
- скорости тел до соударения; и
и  - скорости тел после соударения.
- скорости тел после соударения.Согласно закону сохранения импульса в замкнутой системе
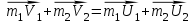 .(2)
.(2)Так как движение происходит по одной прямой, то можно перейти от векторного уравнения (2) к алгебраическому:
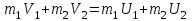 .(2/)
.(2/) Решая систему двух уравнений (1) и (2/) относительно
 и
и  получим
получим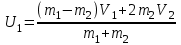 ,
,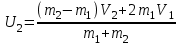 .
.Условимся считать направление движения первого тела положительным.
-
Если тела движутся навстречу друг другу, то и
и 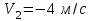 . Тогда
. Тогда
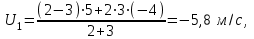
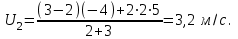
При столкновении тела меняют направления скоростей на обратные.
2. Если первое тело догоняет второе, т.е оба тела движутся в одну сторону, то
 и
и 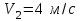 и
и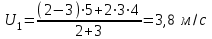 ,
,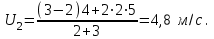
В данном случае после столкновения направление движения тел не меняется.
Б. Тела абсолютно неупругие.
При абсолютно неупругом столкновении нет упругих сил, которые заставили бы столкнувшиеся тела отталкиваться друг от друга. Поэтому после столкновения они будут двигаться вместе с одной скоростью
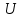 . Из закона сохранения импульса следует
. Из закона сохранения импульса следует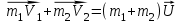 (3)
(3)Так как движение происходит по одной прямой, то можно перейти от векторного уравнения к алгебраическому:
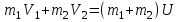 .(3/)
.(3/)откуда
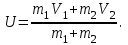
Условимся считать направление движения первого тела положительным.
Если тела движутся навстречу друг другу, т.е. в противоположные стороны, то
 и
и  , следовательно
, следовательно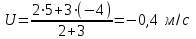
После столкновения тела движутся в ту же сторону, в которую двигалось второе тело, так как числовое значение его импульса было больше, чем у первого тела.
2.Если первое тело догоняет второе, т.е тела движутся в одну сторону, то
 и
и 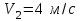 , следовательно
, следовательно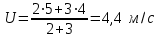
Направление движения тел остается неизменным.
3.При неупругом столкновении часть энергии переходит во внутреннюю