Файл: Курсовая работа По дисциплине Методика преподавания математики Выполнила студентка.docx
Добавлен: 09.12.2023
Просмотров: 186
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
1. Понятие логического мышления
2.2. Возрастные особенности развития логического мышления в старшем и среднем школьном возрасте
3. Развитие логического мышления в условиях введения ФГОС НОО
4. Приемы и методы развития логических учебных действий на уроках математики
5. Примеры приемов развития логический учебных действий на уроках математики
5.1. Характеристика приёмов, способствующих развитию логических УД
5.3. Примеры учебных задач, способствующих развитию логических УД
5. Примеры приемов развития логический учебных действий на уроках математики
5.1. Характеристика приёмов, способствующих развитию логических УД
| Планируемые результаты (логические УД) | Наименование приема | Краткая характеристика | Примеры заданий | ||||||||||||
| Установление причинно-следственных связей | Найди ошибку | Предлагается отыскать ошибку в решении (ответе) одного или нескольких заданий | Некоторая линейная функция задана таблицей:
Задайте ее формулой, если известно, что одно из значений функции записано неверно. | ||||||||||||
| Постройка классификаций на основе дихотомического деления (на основе отрицания) | Математический герой | В урок вводится какой-либо математический герой, который или решает задание, или предлагает его для решения, или придумывает фокус и т. д. | Валера Торопыгин начертил равносторонний прямоугольный треугольник. Не сможете ли вы повторить его успех? | ||||||||||||
| Осуществление сравнений, сериаций, и классификаций, самостоятельно выбирая основания и критерии для указанных логических операций | Обращение | По указанным компонентам и результату отыскать действия или по указанным действиям и результату найти компоненты. | Даны две точки А и В, отмеченные на белом листе бумаги. Начертите такую систему координат, чтобы точки имели следующие координаты: а) А(1; 3), В(-3; 3); б) А(1; 2), В(1; -4). | ||||||||||||
| Осуществление логических операций установления родовидовых отношений, ограничение понятия | Лото | Внимание школьников привлекает необычная форма задания или неожиданная организация выполнения задания | В мешочек помещают шарики с номерами пунктов учебника, которые уже изучены. Класс делится на группы, обычно по рядам. Команды составляют по 4–5 вопросов по каждому пункту. | ||||||||||||
| Обобщение понятий | Восстановление | По части какого-либо математического объекта требуется восстановить весь объект. | Восстановите координатную прямую, часть которой изображена на рисунке. | ||||||||||||
| Постройка логических рассуждений, включающих установление причинно-следственных связей | Тестовые вопросы | Учитель задает кратко вопросы. | 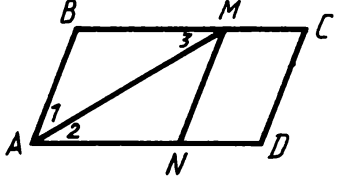 В параллелограмме В параллелограммеABCD (рис. 2) AM – биссектриса угла А, MN\\AB. Известно, что АВ = 10 м, AD = 15 м. Учитель называет отрезок, а ученик быстро говорит, чему равна длина названного отрезка: 1) MN; 2) ВМ; 3) AN; 4) ВС; 5) AN; 6) ND; 7) МС. |
5.2. Приемы развития логических учебных действий через текстовые задачи
| Приемы | Основные характеристики приема |
| Работа над решенной задачей | Многие ученики только после повторного анализа осознают план решения задачи. Это путь к выработке устойчивых логических рассуждений. |
| Решение задач разными способами | Умение решать задачи несколькими способами свидетельствует о достаточно высоком математическом развитии. Развиваются умения самостоятельно выбирать основания и критерии для логических операций. |
| Правильно организован способ анализа задачи | По вопросу или от данных к вопросу. Осуществление логических операций перехода от понятия с меньшим объемом к понятию с большим объёмом. |
| Представление ситуации, описанной в задаче (нарисовать "картинку") | Учитель обращает внимание детей на детали, которые нужно обязательно представить и те, которые можно опустить. Мнимое участие в этой ситуации. Разбивка текста задачи на части. Моделирование ситуации с помощью чертежа, рисунка. |
| Самостоятельное составление задач учениками | Составление задачи, используя слова: больше настолько, меньше в, настолько больше, настолько меньше; решаемую в 1, 2, 3 действия; по данному плану ее решения, действиям и ответу; по выражению и т.д. Логическое УД: обобщение понятий, от части к целому. |
| Решение задач с отсутствующими или лишними данными | Работа над задачей с недостающими и лишними данными развивает у детей умение осмысливать логические связи между искомым и данными. |
| Составление разных выражений по данным задачам и объяснение, которое поясняет то или другое выражение; выбор тех выражений, которые являются ответом на вопрос задачи | Дает возможность развивать правильность и чёткость рассуждений, критическое мышление, развивает у них гибкость, вариативность мышления. |
| Изменение вопроса задачи | Изменение вопроса задачи так, чтобы задача решалась другим действием или так, чтобы действий в решении стало больше (меньше). Формируется логическое УД: осуществление самостоятельного выбора основания и критериев для указанных логических операций. |
| Изменение условия задачи так, чтобы задача решалась другим действием | Обобщение понятий – осуществление логических операций перехода от видовых признаков к родовому понятию. |
| Объяснение готового решения задачи | Повторный анализ – это путь к выработке твердых знаний по математике |
| Использование приема сравнения задач и их решений | Это прием умственной деятельности учащихся, который предполагает установление сходства или различия между объектами изучения |
| Запись двух решений на доске: верного и неверного | Развивает критическое мышление, осуществление сравнений, поиск противоречий. |
| Задание: определить, какой вопрос и какое действие лишние в решении задачи (или, напротив, возобновить пропущенный вопрос и действие в задаче) | Постройка логических рассуждений, включающих установление причинно-следственных связей |
| Составление аналогичной задачи с измененными данными | Такие задачи помогают обобщению знаний о связях между искомым и данными, при этом дети устанавливают, что можно узнать по определенным данным. |
| Решение обратных задач | На решение обратной задачи уходит несравненно меньше времени, чем на решение новой задачи, так как числовые данные и сюжет остаются прежними; производится здесь лишь логическая операция по переосмыслению ролей чисел; неизвестное в прямой задаче становится известным и наоборот. |
| Решение открытых задач | Условие размытое, есть степень неопределенности. Методы решения данных задач разнообразны. В ответе содержится набор возможных ответов. Развивается умение строить логические рассуждения |
5.3. Примеры учебных задач, способствующих развитию логических УД
| Класс | Тема | Этап урока | Задание | |||||||||
| 5 | Десятичная система счисления | Актуализация знаний и пробное учебное действие | Найдите число, у которого: а) цифра десятков больше цифры единиц в 5 раз; б) цифра единиц на 9 меньше цифры десятков. | |||||||||
| 5 | Вычисления с многозначными числами | Актуализация знаний и пробное учебное действие | Тестовые вопросы. На доске записано число 36. Учитель задает вопросы, ученик быстро отвечает.
а) большее 36; б) меньшее 36.
а) двух равных слагаемых; б) двух неравных слагаемых; в) трех равных слагаемых; г) трех неравных слагаемых.
а) двух равных множителей; б) двух неравных множителей.[16] | |||||||||
| 5 5 5 | Числовые и буквенные выражения | Актуализация знаний и пробное учебное действие | Подставьте вместо звездочек такие знаки действий, чтобы равенства были верными: а)4*4*13=13; б) 21 * 8 * 8 = 21 | |||||||||
| Актуализация знаний и пробное учебное действие | Учитель предложил Валере Торопыгину решить следующую задачу: «Купили 20 тетрадей по 3 р. за штуку и 15 линеек по 4 р. за штуку. Сколько стоит вся покупка?» Решая эту задачу, Валера составил числовое выражение: 20–3–15–4. Потом Валера нашел его значение. Получился 0. И Валера записал в ответе: 0. Согласны ли вы с его решением? Что вычислил Валера? [16] | |||||||||||
| 5 | Числовые и буквенные выражения | Актуализация знаний и пробное учебное действие | Даны два буквенных выражения: 9 – х – 7 и 23 – х. Если в эти выражения подставить вместо буквы х некоторое число, то значения полученных числовых выражений будут равны. Найдите это число, если известно, что оно меньше 5. | |||||||||
| 5 | Уравнения | Актуализация знаний и пробное учебное действие | Вместо квадратиков запишите такие числа, чтобы все уравнения имели один и тот же корень 2: а)3х+5=□;б)7х–4=□; в) □ – 11х=12. | |||||||||
| 5 | Числовые и буквенные выражения | Актуализация знаний и пробное учебное действие | Вместо квадратиков запишите такие числа, не равные нулю, чтобы значения полученных числовых выражений было легко вычислить устно: а) 2*78*□; б) 3*□*7*25; в) □*9*125. | |||||||||
| 5 | Уравнения | Развитие умений - применение нового знания. Первичное закрепление с комментированием во внешней речи | Подставьте вместо квадратиков такие числа, кроме 1, чтобы равенства оказались верными: а) □*х*7 = 42х; б) □*4*□*b = 60b; в) □*3*□*а*□ =210а. | |||||||||
| 5 | Обыкновенные дроби | Формулирование проблемы (темы и целей урока). Планирование деятельности | Игровой момент. Учитель. Ребята, у меня в руках веревка. Ее длина 120 см. Мне необходимо от нее отрезать кусок длиной 30 см, но у меня нет под рукой линейки. И все же я могу отрезать требуемый кусок. Кто скажет, как это сделать? Как это сделать, если необходимо отрезать кусок длиной 45 см? | |||||||||
| 5 | Основное свойство дроби | Развитие умений - применение нового знания. Первичное закрепление с комментированием во внешней речи | Валера Торопыгин хвалился, что всего за час нашел число, обладающее удивительным свойством: 2/5 этого числа и 4/10 этого числа были равны! Не могли бы вы за 1 минуту назвать такое число? | |||||||||
| 5 | Определение угла. Развернутый угол | Рефлексия учебной деятельности на уроке (итог урока) | На доске начерчены углы и перепутаны их градусные меры: 180°, 30°, 150°, 90°. Назовите градусную меру каждого из углов. | |||||||||
| 5 | Сложение и вычитание десятичных дробей | Развитие умений - применение нового знания. Первичное закрепление с комментированием во внешней речи | Вместо квадратиков запишите такие числа, чтобы равенства были верными: а) 4,2-□ =3,9; б) □-2,7 = 2,3; в) □-□=3,1; г)□-□=4,75. | |||||||||
| 5 | Понятие процента | Развитие умений - применение нового знания. Первичное закрепление с комментированием во внешней речи | Валера Торопыгин записал два числа. Нашел 1% каждого числа. Полученные числа оказались равны. Может ли такое быть? | |||||||||
| 6 | Сложение и вычитание десятичных дробей | Развитие умений - применение нового знания. Первичное закрепление с комментированием во внешней речи |
Игровой момент. Сумму данных чисел запишите в третью клетку. Сумму чисел, стоящих во второй и третьей клетках, запишите в четвертую клетку и т. д. Кто быстрее найдет число, стоящее в последней клетке? [16] | |||||||||
| 6 | Окружность. Длина окружности | Рефлексия учебной деятельности на уроке (итог урока) | В велосипедном колесе 20 спиц. А сколько будет промежутков между спицами? | |||||||||
| 6 | Противоположные числа. Модуль числа | Рефлексия учебной деятельности на уроке (итог урока) | Однажды Валера Торопыгин в течение целого часа пытался отыскать два противоположных числа, которые оба были бы отрицательны, но безуспешно. Почему? | |||||||||
| 6 | Признаки делимости на 3 и 9 | Формулирование проблемы (темы и целей урока). Планирование деятельности | Игровой момент. Учитель вызывает ученика и предлагает ему записать на доске любое число. Потом без труда между двумя любыми цифрами этого числа записывает такую цифру, что полученное число делится на 9 без остатка. Учащиеся проверяют учителя, выполняя деление | |||||||||
| 6 | Противоположные числа. Модуль числа | Актуализация знаний и пробное учебное действие | Игровой момент. Тестовые вопросы. На доске записано целое отрицательное число, например —19. Ученик должен быстро ответить на вопросы, которые учитель задает в краткой форме.
| |||||||||
| 6 | Правило вычисления значения алгебраической суммы | Развитие умений - применение нового знания. Первичное закрепление с комментированием во внешней речи | Подставьте вместо квадратиков такие числа, чтобы равенства оказались верными: а) 627 +□ =0; б) 315 — 819+□=315; в) □+472+□ =472; г)381-□=-19. | |||||||||
| 6 | Умножение и деление положительных и отрицательных чисел | Актуализация знаний и пробное учебное действие | Замените звездочки знаками действий так, чтобы равенства получились верными: а) -3,2 * 5 = -16; б) -9,1 * (— 10) = 91; в) (-3,2* 7,4)* (-6)= -25,2; г) -1,1 * (-7,3* 2,7)* (-4)= -44. | |||||||||
| 6 | Положительные и отрицательные числа. Координатная прямая | Актуализация знаний и пробное учебное действие | Восстановите координатную прямую, т. е. отметьте точку О, найдите единичный отрезок и направление |
| 6 | Решение задач на составление уравнений | Актуализация знаний и пробное учебное действие | Один ученик решал задачу, которая начиналась словами: «За три дня в магазине было продано 720 кг яблок». Он составил следующее уравнение:x+2x+3x=720. Используя эти данные, сформулируйте задачу полностью и решите ее. | ||||||||||
| 6 | Решение уравнений | Актуализация знаний и пробное учебное действие | Валера Торопыгин, выполняя домашнее задание, решил уравнение так: 15x—30=12x—24; 15(x—2)=12(x—2); 15=12. Ответ: решения нет. В чем его ошибка? | ||||||||||
| 7 | Координатная плоскость | Актуализация знаний и пробное учебное действие | Отметьте на координатной плоскости указанные ниже точки. Они располагаются в определенной последовательности. Догадайтесь в какой и отметьте еще три точки, соблюдая эту последовательность. Назовите координаты этих точек.
D (– 1; 1);
3) Х(-9; -5), Y (-9; -2), Z(-9; -1). | ||||||||||
| 7 7 | Линейная функция и ее график | Актуализация знаний и пробное учебное действие | Чтобы построить график линейной функции, Валера Торопыгин нашел координаты двух точек: А(–3; 3) и В(3; –3). Запишите формулу этой функции. | ||||||||||
| Актуализация знаний и пробное учебное действие | Некоторая линейная функция задана таблицей:
Задайте ее формулой, если известно, что одно из значений функции записано неверно. | ||||||||||||
| 7 | Свойства степени с натуральным показателем | Развитие умений - применение нового знания. Первичное закрепление с комментированием во внешней речи | Игровой момент. Учитель задумывает какую-нибудь степень с основанием а. Ученик называет любую степень с тем же основанием. Учитель либо делит задуманную степень на предложенную, либо умножает и записывает результат. Например, учитель задумал а30. Ученик назвал а11. Учитель пишет на доске: а11→а19. Значит, он мог задумать либо степень а8, либо степень а30. Другой ученик называет степень с тем же основанием, например а5. Учитель пишет: а5→ а35. Значит, он задумал степеньа30 . Ученики должны отгадать задуманную степень. | ||||||||||
| 7 7 | | Актуализация знаний и пробное учебное действие | Задание с продолжением. Запишите степень с основанием с, которую можно представить: 1) в виде квадрата; 2) и в виде куба; 3) и в виде четвертой степени; 4) и в виде пятой степени. | ||||||||||
| Актуализация знаний и пробное учебное действие | Запишите вместо квадратиков такие степени числа 2, чтобы получилось верное равенство: □5 * □6 = □7 . | ||||||||||||
| 7 | Сложение и вычитание одночленов. Умножение одночленов. Возведение одночлена в степень | Актуализация знаний и пробное учебное действие | Тестовые вопросы. На доске записаны одночлены 10m2 и 2m2. Учитель задает вопросы в краткой форме, ученик быстро на них отвечает.
10) Квадрат разности? | ||||||||||
| 7 | Умножение одночленов. | Развитие умений - применение нового знания. Первичное закрепление с комментированием во внешней речи | Стрела
Найдите произведение одночленов х и — 2у и запишите его в третью клетку. Найдите произведение последних двух одночленов и результат запишите в следующую клетку и т. д. Какой одночлен будет в 8-й клетке? | ||||||||||
| 7 | Сложение и вычитание многочленов | Актуализация знаний и пробное учебное действие | В равенствах (11x–10) + (12х–3) =□, (11х–10) – (12x –3) =□ вместо квадратиков запишите такие числа, чтобы полученные уравнения оказались равносильными. | ||||||||||
| 7 7 7 | Треугольники. | Актуализация знаний и пробное учебное действие | В треугольнике ABC АВ=3,2 см,ВС=3,2 см. Каков периметр треугольника, если у него все углы равны? | ||||||||||
| Рефлексия учебной деятельности на уроке (итог урока) | Учитель. У меня в руках два листа бумаги. (Учитель поднимает листы чертежами к себе.) На одном начерчен равносторонний треугольник, а на другом – разносторонний. Задайте только один вопрос и, выслушав ответ, скажите, какой треугольник на каком листе изображен. | ||||||||||||
| Рефлексия учебной деятельности на уроке (итог урока) | Разбейте равносторонний треугольник на: 1) 2; 2) 3; 3) 4; 4) 6 равных треугольников. | ||||||||||||
| 8 | Сложение и вычитание алгебраических дробей с разными знаменателями | Актуализация знаний и пробное учебное действие | Вместо квадратиков запишите такие одночлены, чтобы равенство оказалось тождеством: 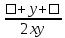 = = 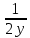 + + 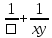 . . | ||||||||||
| 8 | Сложение и вычитание алгебраических дробей с разными знаменателями | Актуализация знаний и пробное учебное действие | Стрела: 1)
Сложение в 5-й клетке? 2)
Умножение в 7-й клетке? 3)
Деление в 7-й клетке? | ||||||||||
| 8 8 | Свойства квадратных корней | Актуализация знаний и пробное учебное действие | Уловите закономерность в следующем ряду чисел: 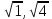 , , 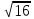 , , 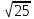 , , 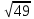 , , 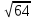 , … и допишите следующие пять чисел. , … и допишите следующие пять чисел. | ||||||||||
| Актуализация знаний и пробное учебное действие | 1) Изобразите число 2 ровно двумя двойками, используя известные действия (можно применять скобки).
| ||||||||||||
| 8 | Квадратные уравнения. | Актуализация знаний и пробное учебное действие | Расшифруйте следующую запись: ах2+Ьх + с = 0; □2 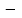 n = 0, n≥0; n = 0, n≥0;□2 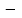 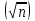 2 =0; 2 =0;□= 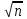 или □=- или □=-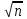 [15]. [15]. | ||||||||||
| 8 | | Актуализация знаний и пробное учебное действие | Валера Торопыгин утверждает, что если в квадратном уравненииax2+bx +c = 0 числа а и с имеют разные знаки, то уравнение имеет корни. Согласны ли вы с ним [13]? | ||||||||||
| 8 | Функция у= х², её свойства и график | Актуализация знаний и пробное учебное действие | Запишите квадратичную функцию, которая: 1)убывает на промежутке (-∞;–5] и возрастает на промежутке [5; + ∞); 2)возрастает на промежутке (-∞; 5] и убывает на промежутке [5; +∞); 3)убывает на промежутке (–∞; –1] и возрастает на промежутке [7; +∞) | ||||||||||
| 8 | Соотношение между сторонами и углами прямоугольного треугольника | Развитие умений - применение нового знания. Первичное закрепление с комментированием во внешней речи | Ассоциация Тригонометрия в ладони. Оказывается, значение синусов и косинусов углов «находятся» на нашей ладони. 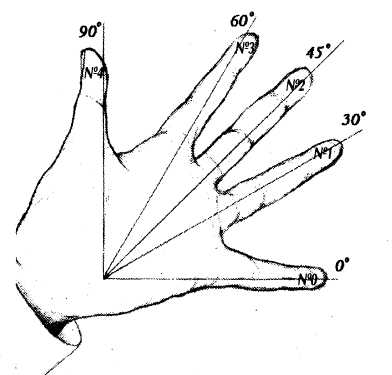  | ||||||||||
| 8 | Параллелограмм и трапеция | Актуализация знаний и пробное учебное действие | В параллелограмме ABCD (рис. 2) AM – биссектриса угла А, MN\\AB. Известно, что АВ= 10 м, AD=15 м. Учитель называет отрезок, а ученик быстро говорит, чему равна длина названного отрезка: 1) MN 2) ВМ; 3) AN; 4) ВС; 5) AN; 6) ND; 7) МС [17].  | ||||||||||
| 8 | Параллелограмм и трапеция | Рефлексия учебной деятельности на уроке (итог урока) | Игровой момент. Учитель. Я начертил трапецию на листе бумаги. Задайте только один вопрос и, выслушав ответ, скажите, будет ли она равнобедренной. | ||||||||||
| 9 | Понятие вектора. | Рефлексия учебной деятельности на уроке (итог урока) | Игровой момент. Учитель. У меня на листе бумаги начерчены два вектора а и Ь. Задайте только один вопрос и, выслушав ответ, скажите: 1) коллинеарны ли они; 2) равны ли они. | ||||||||||
| 9 | Векторы. Метод координат. | Актуализация знаний и пробное учебное действие | Треугольник задан на координатной плоскости своими вершинами А (2; 3), В (–3; 5); С (–1, –2). Не отмечая точек на плоскости, назовите координаты трех точек, лежащих внутри треугольника. Какие стороны треугольника пересекут ось х? ось у? | ||||||||||
| 9 | Простейшие задачи в координатах. | Актуализация знаний и пробное учебное действие | Сформулируйте задание по его решению: 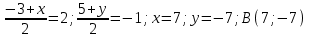 | ||||||||||
| 9 | Функция у= х2п , у=х2п+1 и их графики | Развитие умений - применение нового знания. Первичное закрепление с комментированием во внешней речи | Валера Торопыгин начертил графики функций у = х3и у =х 5, а потом стер оси координат. Назовите координаты точек А, В, С. Графиком какой функции является линия I, линия II?[17] 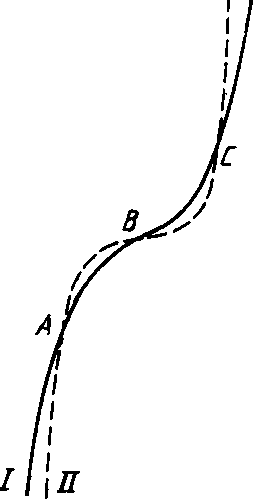 | ||||||||||
| 9 | Функция у=х2, у=х3 и их графики | Актуализация знаний и пробное учебное действие | Дан график функции у = х2. Он пересекается прямой так, что абсциссы точек пересечения равны 2 и –2. Назовите уравнение этой прямой, проведите ее, запишите уравнение, которое будет иметь эти корни (т. е. 2 и –2) [15]. | ||||||||||
| 9 9 | Функции y = xn (nN), их свойства и графики | Рефлексия учебной деятельности на уроке (итог урока) | Учитель. Я задумал степенную функцию с натуральным показателем. Задайте только один вопрос и, выслушав ответ, скажите, эта функция четная или нечетная. | ||||||||||
| Актуализация знаний и пробное учебное действие | Известно, что одно из утверждений о функции f(x)=xn ложно, а другие два истинны.
| ||||||||||||
| 9 9 | Функция у=х2, у=х3 и их графики | Актуализация знаний и пробное учебное действие | Задание с продолжением. Запишите функцию, графиком которой является парабола, и ее ветви опущены вниз, и она проходит через точку (–1; –8). | ||||||||||
| Актуализация знаний и пробное учебное действие | Постройте график квадратичной функции, если известно, что он проходит через точки (–4; 4), (– 2; –3), (0; 4). | ||||||||||||
| 9 9 | Формула п-го члена арифметической прогрессии | Рефлексия учебной деятельности на уроке (итог урока) | Игровой момент. Учитель. Я задумал некоторую арифметическую прогрессию. Задайте мне только два вопроса, чтобы после ответов вы быстро смогли бы назвать 7-й член этой прогрессии. | ||||||||||
| Формулирование проблемы (темы и целей урока). Планирование деятельности | На доске записано 20 чисел: 1, 4, 7, 10, 13, 16, 19, 22, 25, 28, 31, 34, 37, 40, 43, 46, 49, 52, 55, 58. Учитель стоит спиной к доске. Ученики называют номер числа, а учитель мгновенно называет само число. Потом он предлагает учащимся объяснить, как ему это удается. | ||||||||||||
| 9 | Длина окружности. Площадь круга. | Рефлексия учебной деятельности на уроке (итог урока) | Теннисный шарик и баскетбольный мяч обтянуты проволокой «по экватору». Длину проволоки увеличили на 1 см. Где зазор будет больше? |


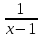
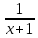
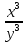
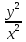
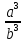
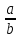
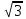 и знаки действий, получите число 6.
и знаки действий, получите число 6.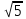 по два раза, получите число 2.
по два раза, получите число 2.