Файл: Учебнометодическое пособие знакомит студентов с основными понятиями о.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 474
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
ВВЕДЕНИЕ
Учебно-методическое пособие знакомит студентов с основными понятиями о теории вероятностей, случайных процессах, статистическом оценивании и проверке гипотез, статистических методах обработки экспериментальных данных, математических методах, принятых в биологических исследованиях.
Пособие состоит из четырех разделов:
-
Введение в теорию вероятностей.
-
Основные понятия и термины статистики.
-
Статистические методы обработки экспериментальных данных.
-
Компьютерная обработка данных анализа в специализированной программе EasyStatistics.
Введение в теорию вероятностей дает представление о случайных событиях, вероятности и ее свойствах, случайных величинах и основных теоретических распределениях случайных величин.
При изучении второго раздела разбираются понятия о совокупности и выборке, классификации признаков, дается представление о схемах научного эксперимента и научных гипотезах, достоверности и надежности результатов.
Третий раздел знакомит со статистическими методами описания групп, способами их сравнения в зависимости от характера распределения исходных данных. Большое внимание уделено корреляционно-регрессионному анализу, лежащему в основе многомерных методов анализа. Разбираются широко распространенные в биологических исследованиях методы оценки динамики, цикличности и классификации. При описании каждого метода описываются условия, необходимые для проведения статистической обработки, и возможные трудности в интерпретации полученных показателей.
Четвертый раздел посвящен практическому применению методов статистической обработки данных с помощью специализированной программы «Статистическая обработка медико-биологических данных» (EasyStatistics). Данная программа разработана автором пособия (Роспатент №2003612171) и предназначена для статистической обработки данных биологических и медицинских исследований и, в первую очередь, нацелена на выполнение курсовых и дипломных работ студентами. В то же время это не замена уже существующим мощным статистическим пакетам, таким как Statistica, а скорее дополнение, помогающее оценить возможности манипулирования данными и принципы работы с основными статистическими методами.
Каждый раздел содержит список вопросов и заданий для самопроверки.
Пособие также содержит список учебно-методических материалов, рекомендуемых для самостоятельной работы студентов.
РАЗДЕЛ I. ВВЕДЕНИЕ В ТЕОРИЮ ВЕРОЯТНОСТЕЙ
Закономерности, которым подчиняются случайные события, изучаются в разделах математики, которые называются теорией вероятностей и математической статистикой.
Понятие о случайном событии
Опыт, эксперимент, наблюдение явления называются испытанием. Испытаниями, например, являются: бросание монеты, выстрел из винтовки, бросание игральной кости (кубика с нанесенными на каждую грань числом очков — от одного до шести).
Результат, исход испытания называется событием.
Для обозначения событий используются большие буквы латинского алфавита: А, В, С и т. д.
Два события называются совместимыми, если появление одного из них не исключает появление другого в одном и том же испытании.
Испытание: однократное бросание игральной кости. Событие А — появление четырех очков. Событие В— появление четного числа очков. События Аи В совместимые.
Два события называются несовместимыми, если появление одного из них исключает появление другого в одном и том же испытании.
Испытание: однократное бросание монеты. Событие А — выпадение герба, событие В — выпадение цифры. Эти события несовместимы, так как появление одного из них исключает появление другого.
Несовместимость более чем двух событий означает их попарную несовместимость
Испытание: однократное бросание игральной кости. Пусть события А1, А2, А3, А4, А5, А6 соответственно выпадение одного очка, двух, трех и т. д. Эти события являются несовместимыми..
Два события А и В называются противоположными, если в данном испытании они несовместимы и одно из них обязательно происходит.
Событие, противоположное событию А, обозначают через А
.
Испытание: бросание монеты. Событие А — выпадение герба, событие В — выпадение цифры. Эти события противоположны, так как исходами бросания могут быть лишь они, и появление одного из них исключает появление другого, т. е. А = В
или А
= В.
Событие называется достоверным, если в данном испытании оно является единственно возможным его исходом, и невозможным, если в данном испытании оно заведомо не может произойти.
Испытание: извлечение шара из урны, в которой все шары белые. Событие А — вынут белый шар — достоверное событие; событие В — вынут черный шар — невозможное событие.
Достоверное и невозможное события в данном испытании являются противоположными.
Событие А называется случайным, если оно объективно может наступить или не наступить в данном испытании.
Выпадение шести очков при бросании игральной кости — случайное событие. Оно может наступить, но может и не наступить в данном испытании.
Прорастание девяноста восьми зерен пшеницы из ста — случайное событие. Это событие может наступить, но, может быть, прорастет зерен больше или меньше.
Классическое определение вероятности
Всякое испытание влечет за собой некоторую совокупность исходов — результатов испытания, т. е. событий. Во многих случаях возможно перечислить все события, которые могут быть исходами данного испытания.
Говорят, что совокупность событий образует полную группу событий для данного испытания, если его результатом обязательно становится хотя бы одно из них.
События Ul, U2, ..., Un , образующие полную группу попарно несовместимых и равновозможных событий, будем называть элементарными событиями.
Вернемся к опыту с подбрасыванием игральной кости. Пусть Ui — событие, состоящее в том, что кость выпала гранью с цифрой i. Как уже отмечалось, события U1, U2, …, U6 образуют полную группу попарно несовместимых событий. Так как кость предполагается однородной и симметричной, то события U1, U2, …, U6 являются и равновозможными, т. е. элементарными.
Событие А называется благоприятствующим событию В, если наступление события А влечет за собой наступление события В.
Пусть при бросании игральной кости события U2, U4 и U6 — появление соответственно двух, четырех и шести очков и А — событие, состоящее в появлении четного очка; события U2, U4 и U6 благоприятствуют событию А.
Классическое определение вероятности
Вероятностью Р (А) события А называется отношение m/n числа элементарных событий, благоприятствующих событию А, к числу всех элементарных событий, т. е.
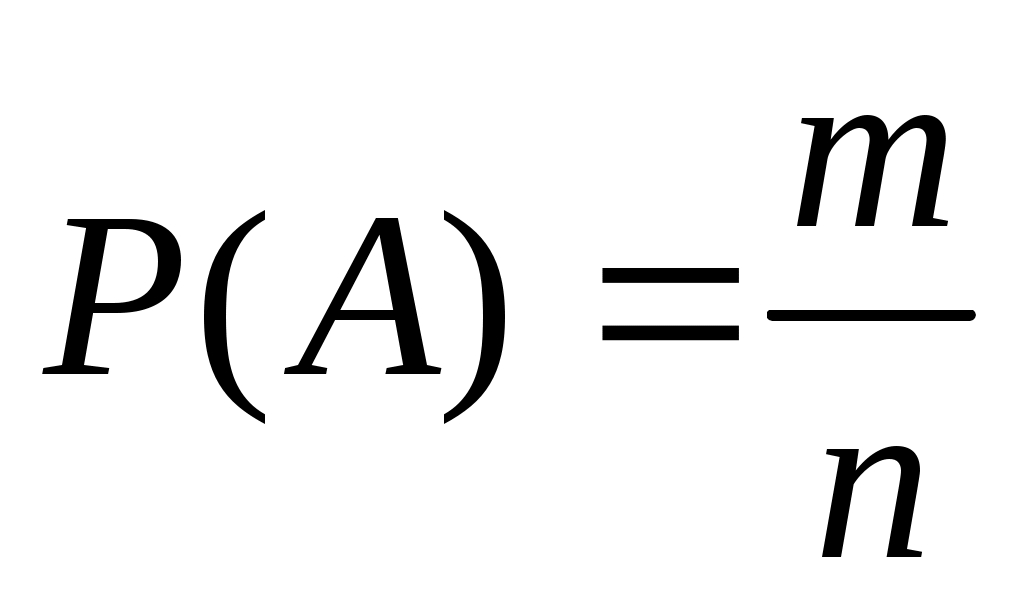
Вычислим вероятность выпадения герба при одном бросании монеты. Очевидно, событие А — выпадение герба и событие В — выпадение цифры — образуют полную группу несовместимых и равновозможных событий для данного испытания. Значит, здесь n = 2. Событию А благоприятствует лишь одно событие — само А, т. е. здесь m = 1. Поэтому Р(А) = 0,5.
Найти вероятность того, что при бросании игральной кости выпадет число очков, делящееся на 2 (событие А). Число элементарных событий здесь 6. Число благоприятствующих элементарных событий 3 (выпадение 2, 4 и 6).
Поэтому 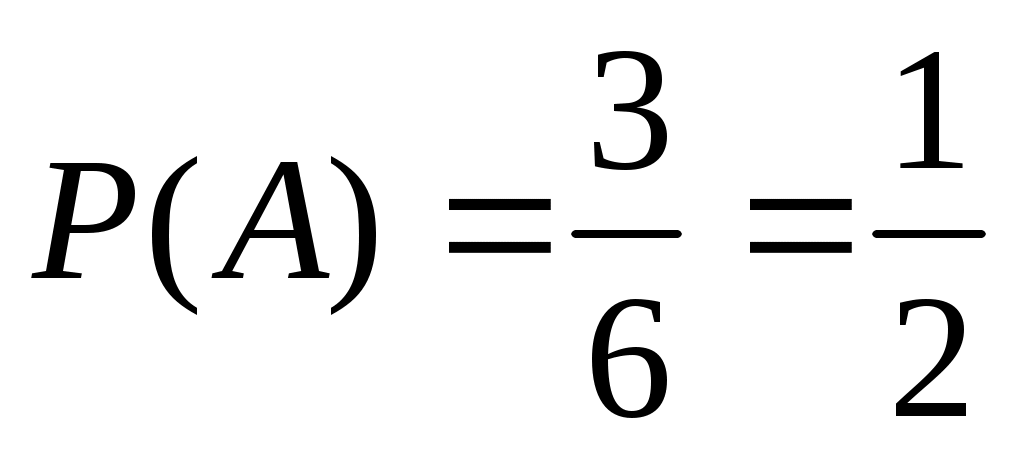 .
.
Из приведенного классического определения вероятности вытекают следующие ее свойства.
1. Вероятность достоверного события равна единице.
Действительно, достоверному событию должны благоприятствовать все n элементарных событий, т. е. m = n и, следовательно, P(A)=1.
2. Вероятность невозможного события равна нулю. В самом деле, невозможному событию не может благоприятствовать ни одно из элементарных событий, т. е. m = 0, откуда P(A)=0.
3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей.
Действительно, случайному событию благоприятствует лишь часть из общего числа элементарных событий. Поэтому в этом случае 0 < m < n , значит, 0 <= Р (А)<= 1.
Относительная частота.
Статистическое определение вероятности.
Классическое определение вероятности не является пригодным для изучения произвольных случайных событий. Так, оно неприемлемо, если результаты испытания не равновозможны. Например, при бросании неправильной игральной кости выпадение ее различных граней не равновозможно.
В таких случаях используется так называемое статистическое определение вероятности.
Пусть произведено n испытаний, при этом некоторое событие А наступило m раз. Число m называется абсолютной частотой (или просто частотой) события А, а отношение 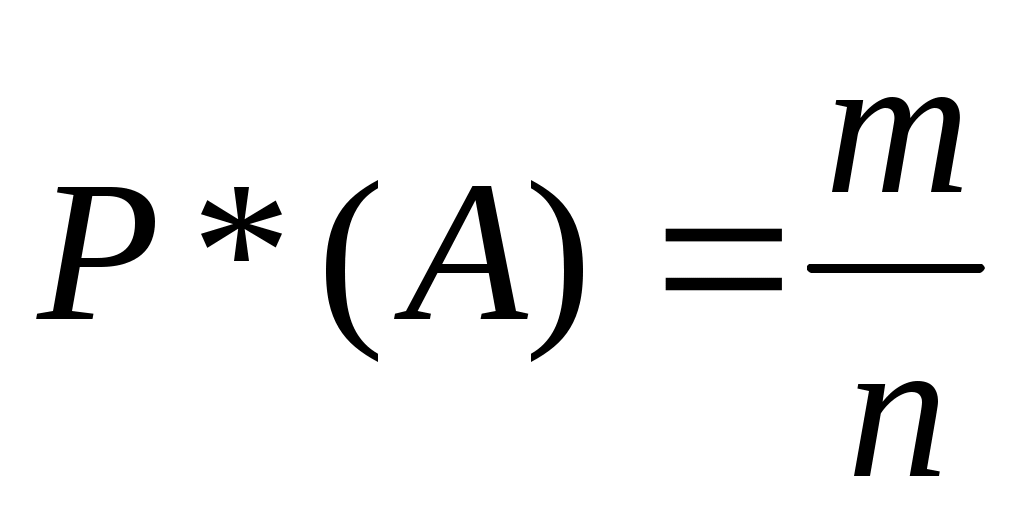 называется относительной частотой события А.
называется относительной частотой события А.
При транспортировке из 10 000 арбузов испортилось 26. Здесь m= 26 — абсолютная частота испорченных арбузов, а P*(A)=0,0026 относительная.
Результаты многочисленных опытов и наблюдений помогают заключить: при проведении серий из n испытаний, когда число n сравнительно мало, относительная частота Р*(A) принимает значения, которые могут довольно сильно отличаться друг от друга. Но с увеличением n — числа испытаний в сериях — относительная частота Р*(А) приближается к некоторому числу Р(А), стабилизируясь возле него и принимая все более устойчивые значения.
Было проведено 10 серий бросаний монеты, по 1000 бросаний в каждой. Относительные частоты выпадения герба оказались равными 0,501; 0,485; 0,509; 0,536; 0,485; 0,488; 0,500;0,497; 0,494; 0,484. Эти частоты группируются около числа 0,5
Статистическое определение вероятности
Вероятностью события А в данном испытании называется число Р (А), около которого группируются значения относительной частоты при больших n.
По официальным данным шведской статистики, относительные частоты рождения девочек по месяцам 2007 г. характеризуются следующими числами (расположены в порядке следования месяцев, начиная с января): 0,486; 0,489; 0,490; 0,471; 0,478; 0,482; 0,462; 0,484; 0,485; 0,491; 0,482; 0,473. Эти частоты группируются около числа 0,482.
Таким образом, относительная частота события приближенно совпадает с его вероятностью, если число испытаний достаточно велико.
Геометрическая вероятность
До этого мы рассматривали возможные эксперименты, в которых реализуется конечное множество событий. Однако существует большое количество задач, для которых такое предположение не является справедливым. При решении таких задач предполагается, что множество реализуемых событий может быть представлено в виде некоторой геометрической фигуры, а конкретное событие соответствует точке заданной части этой фигуры.
В качестве события A можно рассмотреть любую подобласть области Ω. Например, фигуру внутри исходной фигуры на плоскости или отрезок, лежащий внутри исходного отрезка на прямой.
Заметим, что элементарным событием на таком множестве может быть только точка. В самом деле, если множество содержит более одной точки, его можно разбить на два непустых подмножества. Следовательно, такое множество уже неэлементарно.
Теперь определим вероятность. Тут тоже все легко: вероятность «попадания» в каждую конкретную точку равна нулю. Иначе получим бесконечную сумму одинаковых положительных слагаемых (ведь элементарные события равновероятны), которые в сумме больше P(Ω) = 1.
Итак, элементарные события для бесконечных областей Ω — это отдельные точки, причем вероятность «попадания» в любую из них равна нулю. Но как искать вероятность неэлементарного события, которое, подобно Ω, содержит бесконечное множество точек? Вот мы и пришли к определению геометрической вероятности.
Геометрическая вероятность события A, являющегося подмножеством множества Ω точек на прямой или плоскости — это отношение площади фигуры A к площади всего множества Ω.
Мишень имеет форму окружности. Какова вероятность попадания в ее правую половину, если попадание в любую точку мишени равновероятно? При этом промахи мимо мишени исключены.
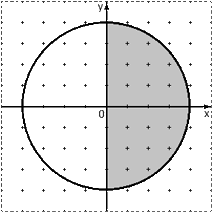
Взглянем на картинку: нас устроит любая точка из правого полукруга. Очевидно, площадь S(A) этого полукруга составляет ровно половину площади всего круга, поэтому имеем
P=0,5
Студент и студентка договариваются о встрече на заданном промежутке времени Т. Тот, кто приходит первым ожидает другого в течение времени t
В качестве множества элементарных событий рассмотри квадрат, состоящий из точек (x,y), 0<=x<=T, 0<=y<=T, где x и у время прихода его и ее.
Благоприятсвующие события образуют точки, для которых |x-y|<t, т.е. точки квадрата между прямыми y=x-t, y=x+t. Площадь получающейся фигуры равна T2-(T-t)2, а площадь всего квадрата – Т2. Отсуда искомая вероятность 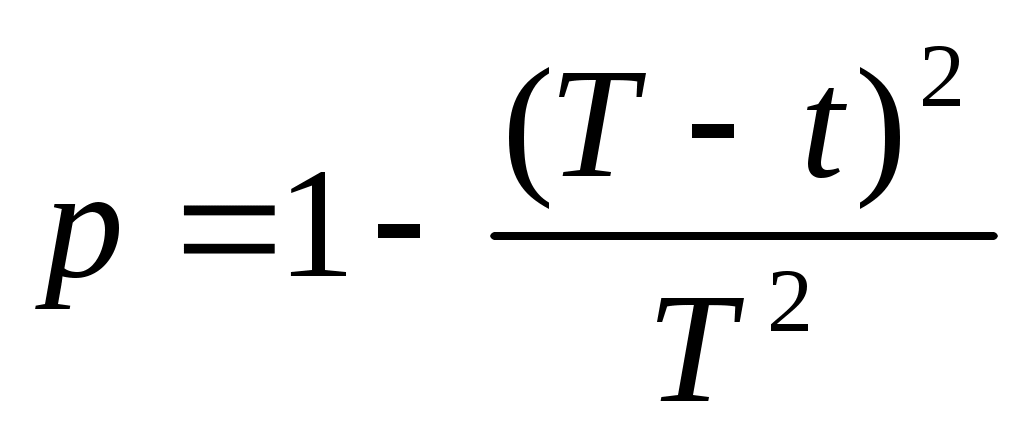
Свойства вероятностей
Сложение вероятностей несовместимых событий
Суммой событий А и В называется событие С = А + В, состоящее в наступлении по крайней мере одного из событий А или В.
Стрельба двух стрелков (каждый делает по одному выстрелу). Событие А — попадание в мишень первым стрелком, событие В — попадание в мишень вторым стрелком. Суммой событий А и В будет событие С = А + В, состоящее в попадании в мишень по крайней мере одним стрелком.
Произведением событий А и В называется событие С = АВ, состоящее в том, что в результате испытания произошло и событие А, и событие В.
Аналогично произведением конечного числа событий A1 А2, …, Ak называется событие А = А1 * A2 * ... * Ak, состоящее в том, что в результате испытания произошли все указанные события.
В условиях предыдущего примера произведением событий А и В будет событие С = АВ, состоящее в попадании в мишень двух стрелков.
Из определения непосредственно следует, что АВ = ВА.
Вероятность суммы двух несовместимых событий А и В равна сумме вероятностей этих событий:
Р (А + В) = Р (А) + Р (В).
Следствие. Сумма вероятностей противоположных событий А и А
равна единице:
Р(А) + Р(А
)=1.
ВВЕДЕНИЕ
Учебно-методическое пособие знакомит студентов с основными понятиями о теории вероятностей, случайных процессах, статистическом оценивании и проверке гипотез, статистических методах обработки экспериментальных данных, математических методах, принятых в биологических исследованиях.
Пособие состоит из четырех разделов:
-
Введение в теорию вероятностей.
-
Основные понятия и термины статистики.
-
Статистические методы обработки экспериментальных данных.
-
Компьютерная обработка данных анализа в специализированной программе EasyStatistics.
Введение в теорию вероятностей дает представление о случайных событиях, вероятности и ее свойствах, случайных величинах и основных теоретических распределениях случайных величин.
При изучении второго раздела разбираются понятия о совокупности и выборке, классификации признаков, дается представление о схемах научного эксперимента и научных гипотезах, достоверности и надежности результатов.
Третий раздел знакомит со статистическими методами описания групп, способами их сравнения в зависимости от характера распределения исходных данных. Большое внимание уделено корреляционно-регрессионному анализу, лежащему в основе многомерных методов анализа. Разбираются широко распространенные в биологических исследованиях методы оценки динамики, цикличности и классификации. При описании каждого метода описываются условия, необходимые для проведения статистической обработки, и возможные трудности в интерпретации полученных показателей.
Четвертый раздел посвящен практическому применению методов статистической обработки данных с помощью специализированной программы «Статистическая обработка медико-биологических данных» (EasyStatistics). Данная программа разработана автором пособия (Роспатент №2003612171) и предназначена для статистической обработки данных биологических и медицинских исследований и, в первую очередь, нацелена на выполнение курсовых и дипломных работ студентами. В то же время это не замена уже существующим мощным статистическим пакетам, таким как Statistica, а скорее дополнение, помогающее оценить возможности манипулирования данными и принципы работы с основными статистическими методами.
Каждый раздел содержит список вопросов и заданий для самопроверки.
Пособие также содержит список учебно-методических материалов, рекомендуемых для самостоятельной работы студентов.
РАЗДЕЛ I. ВВЕДЕНИЕ В ТЕОРИЮ ВЕРОЯТНОСТЕЙ
Закономерности, которым подчиняются случайные события, изучаются в разделах математики, которые называются теорией вероятностей и математической статистикой.
Понятие о случайном событии
Опыт, эксперимент, наблюдение явления называются испытанием. Испытаниями, например, являются: бросание монеты, выстрел из винтовки, бросание игральной кости (кубика с нанесенными на каждую грань числом очков — от одного до шести).
Результат, исход испытания называется событием.
Для обозначения событий используются большие буквы латинского алфавита: А, В, С и т. д.
Два события называются совместимыми, если появление одного из них не исключает появление другого в одном и том же испытании.
Испытание: однократное бросание игральной кости. Событие А — появление четырех очков. Событие В— появление четного числа очков. События Аи В совместимые.
Два события называются несовместимыми, если появление одного из них исключает появление другого в одном и том же испытании.
Испытание: однократное бросание монеты. Событие А — выпадение герба, событие В — выпадение цифры. Эти события несовместимы, так как появление одного из них исключает появление другого.
Несовместимость более чем двух событий означает их попарную несовместимость
Испытание: однократное бросание игральной кости. Пусть события А1, А2, А3, А4, А5, А6 соответственно выпадение одного очка, двух, трех и т. д. Эти события являются несовместимыми..
Два события А и В называются противоположными, если в данном испытании они несовместимы и одно из них обязательно происходит.
Событие, противоположное событию А, обозначают через А
.
Испытание: бросание монеты. Событие А — выпадение герба, событие В — выпадение цифры. Эти события противоположны, так как исходами бросания могут быть лишь они, и появление одного из них исключает появление другого, т. е. А = В
или А
= В.
ВВЕДЕНИЕ
Учебно-методическое пособие знакомит студентов с основными понятиями о теории вероятностей, случайных процессах, статистическом оценивании и проверке гипотез, статистических методах обработки экспериментальных данных, математических методах, принятых в биологических исследованиях.
Пособие состоит из четырех разделов:
-
Введение в теорию вероятностей.
-
Основные понятия и термины статистики.
-
Статистические методы обработки экспериментальных данных.
-
Компьютерная обработка данных анализа в специализированной программе EasyStatistics.
Введение в теорию вероятностей дает представление о случайных событиях, вероятности и ее свойствах, случайных величинах и основных теоретических распределениях случайных величин.
При изучении второго раздела разбираются понятия о совокупности и выборке, классификации признаков, дается представление о схемах научного эксперимента и научных гипотезах, достоверности и надежности результатов.
Третий раздел знакомит со статистическими методами описания групп, способами их сравнения в зависимости от характера распределения исходных данных. Большое внимание уделено корреляционно-регрессионному анализу, лежащему в основе многомерных методов анализа. Разбираются широко распространенные в биологических исследованиях методы оценки динамики, цикличности и классификации. При описании каждого метода описываются условия, необходимые для проведения статистической обработки, и возможные трудности в интерпретации полученных показателей.
Четвертый раздел посвящен практическому применению методов статистической обработки данных с помощью специализированной программы «Статистическая обработка медико-биологических данных» (EasyStatistics). Данная программа разработана автором пособия (Роспатент №2003612171) и предназначена для статистической обработки данных биологических и медицинских исследований и, в первую очередь, нацелена на выполнение курсовых и дипломных работ студентами. В то же время это не замена уже существующим мощным статистическим пакетам, таким как Statistica, а скорее дополнение, помогающее оценить возможности манипулирования данными и принципы работы с основными статистическими методами.
Каждый раздел содержит список вопросов и заданий для самопроверки.
Пособие также содержит список учебно-методических материалов, рекомендуемых для самостоятельной работы студентов.
РАЗДЕЛ I. ВВЕДЕНИЕ В ТЕОРИЮ ВЕРОЯТНОСТЕЙ
Закономерности, которым подчиняются случайные события, изучаются в разделах математики, которые называются теорией вероятностей и математической статистикой.
Понятие о случайном событии
Опыт, эксперимент, наблюдение явления называются испытанием. Испытаниями, например, являются: бросание монеты, выстрел из винтовки, бросание игральной кости (кубика с нанесенными на каждую грань числом очков — от одного до шести).
Результат, исход испытания называется событием.
Для обозначения событий используются большие буквы латинского алфавита: А, В, С и т. д.
Два события называются совместимыми, если появление одного из них не исключает появление другого в одном и том же испытании.
Испытание: однократное бросание игральной кости. Событие А — появление четырех очков. Событие В— появление четного числа очков. События Аи В совместимые.
Два события называются несовместимыми, если появление одного из них исключает появление другого в одном и том же испытании.
Испытание: однократное бросание монеты. Событие А — выпадение герба, событие В — выпадение цифры. Эти события несовместимы, так как появление одного из них исключает появление другого.
Несовместимость более чем двух событий означает их попарную несовместимость
Испытание: однократное бросание игральной кости. Пусть события А1, А2, А3, А4, А5, А6 соответственно выпадение одного очка, двух, трех и т. д. Эти события являются несовместимыми..
Два события А и В называются противоположными, если в данном испытании они несовместимы и одно из них обязательно происходит.
Событие, противоположное событию А, обозначают через А
.Введение в теорию вероятностей.
Основные понятия и термины статистики.
Статистические методы обработки экспериментальных данных.
Компьютерная обработка данных анализа в специализированной программе EasyStatistics.
Испытание: бросание монеты. Событие А — выпадение герба, событие В — выпадение цифры. Эти события противоположны, так как исходами бросания могут быть лишь они, и появление одного из них исключает появление другого, т. е. А = В
Событие называется достоверным, если в данном испытании оно является единственно возможным его исходом, и невозможным, если в данном испытании оно заведомо не может произойти.
Испытание: извлечение шара из урны, в которой все шары белые. Событие А — вынут белый шар — достоверное событие; событие В — вынут черный шар — невозможное событие.
Достоверное и невозможное события в данном испытании являются противоположными.
Событие А называется случайным, если оно объективно может наступить или не наступить в данном испытании.
Выпадение шести очков при бросании игральной кости — случайное событие. Оно может наступить, но может и не наступить в данном испытании.
Прорастание девяноста восьми зерен пшеницы из ста — случайное событие. Это событие может наступить, но, может быть, прорастет зерен больше или меньше.
Классическое определение вероятности
Всякое испытание влечет за собой некоторую совокупность исходов — результатов испытания, т. е. событий. Во многих случаях возможно перечислить все события, которые могут быть исходами данного испытания.
Говорят, что совокупность событий образует полную группу событий для данного испытания, если его результатом обязательно становится хотя бы одно из них.
События Ul, U2, ..., Un , образующие полную группу попарно несовместимых и равновозможных событий, будем называть элементарными событиями.
Вернемся к опыту с подбрасыванием игральной кости. Пусть Ui — событие, состоящее в том, что кость выпала гранью с цифрой i. Как уже отмечалось, события U1, U2, …, U6 образуют полную группу попарно несовместимых событий. Так как кость предполагается однородной и симметричной, то события U1, U2, …, U6 являются и равновозможными, т. е. элементарными.
Событие А называется благоприятствующим событию В, если наступление события А влечет за собой наступление события В.
Пусть при бросании игральной кости события U2, U4 и U6 — появление соответственно двух, четырех и шести очков и А — событие, состоящее в появлении четного очка; события U2, U4 и U6 благоприятствуют событию А.
Классическое определение вероятности
Вероятностью Р (А) события А называется отношение m/n числа элементарных событий, благоприятствующих событию А, к числу всех элементарных событий, т. е.
Вычислим вероятность выпадения герба при одном бросании монеты. Очевидно, событие А — выпадение герба и событие В — выпадение цифры — образуют полную группу несовместимых и равновозможных событий для данного испытания. Значит, здесь n = 2. Событию А благоприятствует лишь одно событие — само А, т. е. здесь m = 1. Поэтому Р(А) = 0,5.
Найти вероятность того, что при бросании игральной кости выпадет число очков, делящееся на 2 (событие А). Число элементарных событий здесь 6. Число благоприятствующих элементарных событий 3 (выпадение 2, 4 и 6).
Поэтому
Из приведенного классического определения вероятности вытекают следующие ее свойства.
1. Вероятность достоверного события равна единице.
Действительно, достоверному событию должны благоприятствовать все n элементарных событий, т. е. m = n и, следовательно, P(A)=1.
2. Вероятность невозможного события равна нулю. В самом деле, невозможному событию не может благоприятствовать ни одно из элементарных событий, т. е. m = 0, откуда P(A)=0.
3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей.
Действительно, случайному событию благоприятствует лишь часть из общего числа элементарных событий. Поэтому в этом случае 0 < m < n , значит, 0 <= Р (А)<= 1.
Относительная частота.
Статистическое определение вероятности.
Классическое определение вероятности не является пригодным для изучения произвольных случайных событий. Так, оно неприемлемо, если результаты испытания не равновозможны. Например, при бросании неправильной игральной кости выпадение ее различных граней не равновозможно.
В таких случаях используется так называемое статистическое определение вероятности.
Пусть произведено n испытаний, при этом некоторое событие А наступило m раз. Число m называется абсолютной частотой (или просто частотой) события А, а отношение
При транспортировке из 10 000 арбузов испортилось 26. Здесь m= 26 — абсолютная частота испорченных арбузов, а P*(A)=0,0026 относительная.
Результаты многочисленных опытов и наблюдений помогают заключить: при проведении серий из n испытаний, когда число n сравнительно мало, относительная частота Р*(A) принимает значения, которые могут довольно сильно отличаться друг от друга. Но с увеличением n — числа испытаний в сериях — относительная частота Р*(А) приближается к некоторому числу Р(А), стабилизируясь возле него и принимая все более устойчивые значения.
Было проведено 10 серий бросаний монеты, по 1000 бросаний в каждой. Относительные частоты выпадения герба оказались равными 0,501; 0,485; 0,509; 0,536; 0,485; 0,488; 0,500;0,497; 0,494; 0,484. Эти частоты группируются около числа 0,5
Статистическое определение вероятности
Вероятностью события А в данном испытании называется число Р (А), около которого группируются значения относительной частоты при больших n.
По официальным данным шведской статистики, относительные частоты рождения девочек по месяцам 2007 г. характеризуются следующими числами (расположены в порядке следования месяцев, начиная с января): 0,486; 0,489; 0,490; 0,471; 0,478; 0,482; 0,462; 0,484; 0,485; 0,491; 0,482; 0,473. Эти частоты группируются около числа 0,482.
Таким образом, относительная частота события приближенно совпадает с его вероятностью, если число испытаний достаточно велико.
Геометрическая вероятность
До этого мы рассматривали возможные эксперименты, в которых реализуется конечное множество событий. Однако существует большое количество задач, для которых такое предположение не является справедливым. При решении таких задач предполагается, что множество реализуемых событий может быть представлено в виде некоторой геометрической фигуры, а конкретное событие соответствует точке заданной части этой фигуры.
В качестве события A можно рассмотреть любую подобласть области Ω. Например, фигуру внутри исходной фигуры на плоскости или отрезок, лежащий внутри исходного отрезка на прямой.
Заметим, что элементарным событием на таком множестве может быть только точка. В самом деле, если множество содержит более одной точки, его можно разбить на два непустых подмножества. Следовательно, такое множество уже неэлементарно.
Теперь определим вероятность. Тут тоже все легко: вероятность «попадания» в каждую конкретную точку равна нулю. Иначе получим бесконечную сумму одинаковых положительных слагаемых (ведь элементарные события равновероятны), которые в сумме больше P(Ω) = 1.
Итак, элементарные события для бесконечных областей Ω — это отдельные точки, причем вероятность «попадания» в любую из них равна нулю. Но как искать вероятность неэлементарного события, которое, подобно Ω, содержит бесконечное множество точек? Вот мы и пришли к определению геометрической вероятности.
Геометрическая вероятность события A, являющегося подмножеством множества Ω точек на прямой или плоскости — это отношение площади фигуры A к площади всего множества Ω.
Мишень имеет форму окружности. Какова вероятность попадания в ее правую половину, если попадание в любую точку мишени равновероятно? При этом промахи мимо мишени исключены.

Взглянем на картинку: нас устроит любая точка из правого полукруга. Очевидно, площадь S(A) этого полукруга составляет ровно половину площади всего круга, поэтому имеем
P=0,5
Студент и студентка договариваются о встрече на заданном промежутке времени Т. Тот, кто приходит первым ожидает другого в течение времени t
В качестве множества элементарных событий рассмотри квадрат, состоящий из точек (x,y), 0<=x<=T, 0<=y<=T, где x и у время прихода его и ее.
Благоприятсвующие события образуют точки, для которых |x-y|<t, т.е. точки квадрата между прямыми y=x-t, y=x+t. Площадь получающейся фигуры равна T2-(T-t)2, а площадь всего квадрата – Т2. Отсуда искомая вероятность
Свойства вероятностей
Сложение вероятностей несовместимых событий
Суммой событий А и В называется событие С = А + В, состоящее в наступлении по крайней мере одного из событий А или В.
Стрельба двух стрелков (каждый делает по одному выстрелу). Событие А — попадание в мишень первым стрелком, событие В — попадание в мишень вторым стрелком. Суммой событий А и В будет событие С = А + В, состоящее в попадании в мишень по крайней мере одним стрелком.
Произведением событий А и В называется событие С = АВ, состоящее в том, что в результате испытания произошло и событие А, и событие В.
Аналогично произведением конечного числа событий A1 А2, …, Ak называется событие А = А1 * A2 * ... * Ak, состоящее в том, что в результате испытания произошли все указанные события.
В условиях предыдущего примера произведением событий А и В будет событие С = АВ, состоящее в попадании в мишень двух стрелков.
Из определения непосредственно следует, что АВ = ВА.
Вероятность суммы двух несовместимых событий А и В равна сумме вероятностей этих событий:
Р (А + В) = Р (А) + Р (В).
Следствие. Сумма вероятностей противоположных событий А и А
В урне 10 шаров: 3 красных, 5 синих и 2 белых. Какова вероятность вынуть цветной шар, если вынимается один шар? Вероятность вынуть красный шар Р(А) = 0,3, синий Р (В) =0,5.
Так как события А и В несовместимы, то по теореме имеем P(A+B)=0,8.
На клумбе растут 20 красных, 30 синих и 40 белых астр. Какова вероятность сорвать в темноте окрашенную астру, если рвется одна астра? Искомая вероятность равна сумме вероятностей сорвать красную или синюю астру, т. е. 20/90+30/90=50/90=5/9.
Умножение вероятностей
Два события А и В называются независимыми, если вероятность появления каждого из них не зависит от того, появилось другое событие или нет. В противном случае события А и В называют зависимыми.
Пусть в урне находятся 2 белых и 2 черных шара. Пусть событие А — вынут белый шар. Очевидно, Р (А) =0,5. После первого испытания вынутый шар кладется обратно в урну, шары перемешиваются и снова вынимается шар. Событие В — во втором испытании вынут белый шар — также имеет вероятность р (В) =0,5 , т. е. события А и В — независимые.
Предположим теперь, что вынутый шар в первом испытании не кладется обратно в урну. Тогда если произошло событие А, т. е. в первом испытании вынут белый шар, то вероятность события В уменьшается (P(В) = 1/3); если в первом испытании был вынут черный шар, то вероятность события В увеличивается (Р(В) = 2/3 ) Итак, вероятность события В существенно зависит от того, произошло или не произошло событие А; в таких случаях события А и В — зависимые.
Пусть А и В — зависимые события. Условной вероятностью РA(В) события В называется вероятность события В, найденная в предположении, что событие А уже наступило.
Если события А и В независимы, то РА(В) =Р(В).
Вероятность произведения двух зависимых событий А и В равна произведению вероятности одного из них на условную вероятность другого, найденную в предположении, что первое событие уже наступило:
Р (АВ) = Р (А)РА(В).
Р (ВА) = Р (В)РВ(А).
Р (А)РА(В) = Р (В)РB(А).
Вероятность произведения двух независимых событий А и В равна произведению вероятностей этих событий:
Р (АВ) = Р (А) Р (В).
Найти вероятность одновременного поражения цели двумя орудиями, если вероятность поражения цели первым орудием (событие А) равна 0,8, а вторым (событие В) — 0,7.
События А и В независимы, поэтому искомая вероятность Р(АВ) = 0,7 • 0,8 = 0,56.
Сложение вероятностей совместимых событий
Вероятность суммы двух совместимых событий A и В равна сумме вероятностей этих событий минус вероятность их произведения:
Р(А + В) = Р(А) + Р (В) — Р(АВ).
Вероятности попадания в цель при стрельбе первого и второго орудий соответственно равны: Р(А)=0,7 и Р(В)=0,8. Найти вероятность попадания при одном залпе (из обоих орудий) хотя бы одним из орудий.
Очевидно, события А к В совместимы и независимы. Поэтому
Р (А + В) =Р (А) +Р (В) - Р (АВ) = 0,7 + 0,8 - 0,7* 0,8 = 1,5 — 0,56 = 0,94.
Замечание. Если события А и В несовместимы, то их произведение АВ есть невозможное событие и, следовательно, Р (АВ) = 0.
Формула полной вероятности
Вероятность события А, которое может наступить лишь при условии появления одного из n попарно несовместимых событий В1, В2, ..., Вn образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А:
Р (А) = Р (В1) PB1 (А) + Р (В2)РВ2 (А) + ... + Р (Вn)РBn(А)
Имеются три одинаковых по виду ящика. В первом находятся две белые мыши и одна серая, во втором — три белые и одна серая, в третьем — две белые и две серые мыши. Какова вероятность того, что из наугад выбранного ящика будет извлечена белая мышь?
Обозначим В1 — выбор первого ящика, В2 — выбор второго ящика, B3 — выбор третьего ящика, А — извлечение белой мыши.
Так как все ящики одинаковы, то Р (B1)= Р (B2) = Р (B3) = 1/3.
Если выбран первый ящик, то Рв1 (А) = 2/3. Аналогично Рв2 (А) =3/4, Рв3(А) = 0,5. Наконец, по формуле получаем:
В группе студентов 4 отличника, 13 хорошо успевающих и 8 слабых студентов. Результаты предшествующих экзаменационных сессий показали, что отличники получают только отличные оценки (потому они и отличники); «хорошисты», как правило, в девяти случав из десяти получают отличные или хорошие оценки; наконец слабые студенты в одном случае из пяти получают хорошие оценки.
Для сдачи экзамена выбирается один студент. Найти вероятность события А, что студент получит хорошую или отличную оценку.
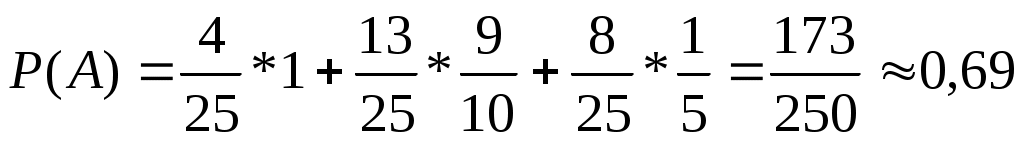
Основные формулы комбинаторики
Комбинаторика — раздел математики, изучающий вопросы о том, сколько комбинаций определенного типа можно составить из данных предметов (элементов).
Как при решении задач с использованием классического определения вероятности, так и в дальнейшем нам понадобятся некоторые формулы комбинаторики. Приведем наиболее употребительные из них.
Размещениями из n различных элементов по m элементов (m х n) называются комбинации, составленные из данных n элементов по m элементов, которые отличаются либо самими элементами, либо порядком элементов.
Например, из трех элементов а, b, с можно составить по два элемента следующие размещения:
ab, ас, ba, bc, ca, cb.
Число различных размещений из n элементов по m элементов определяется с помощью формулы
Сколько можно составить сигналов из 6 флажков различного цвета, взятых по 2? Искомое число сигналов 5*6=30.
Перестановками из n различных элементов называются размещения из этих n элементов по n.
Перестановки можно считать частным случаем размещений при m = n. Следовательно, число всех перестановок из n элементов вычисляется по формуле Рn = n(n - 1)(n - 2) ... 3 • 2 • 1 = n!
Сколько трехзначных чисел можно составить из цифр 1, 2, 3, если каждая цифра входит в изображение числа только один раз? Искомое число трехзначных чисел Р = 3! = 1 *2*3 = 6.
Сочетаниями из n различных элементов по m элементов называются комбинации, составленные из данных n элементов по m элементов, которые отличаются хотя бы одним элементом.
Отметим разницу между сочетаниями и размещениями: в первых не учитывается порядок элементов.
Число сочетаний из п элементов по m элементов вычисляется по формуле
Отметим особенность формулы:
Этой особенностью удобно пользоваться, когда m > n/2.
Сколькими способами можно выбрать две детали из ящика, содержащего 10 деталей? Искомое число способов
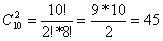
Приведем, наконец, один из примеров применения формул комбинаторики к нахождению вероятности события.
Набирая номер телефона, абонент забыл две последние цифры и, помня лишь, что эти цифры различны, набрал их наудачу. Какова вероятность того, что номер набран правильно?
Две последние цифры можно набрать
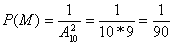
Дискретные и непрерывные случайные величины.
Понятие «случайные величины»
Случайной величиной называется переменная величина, которая в зависимости от исхода испытания случайно принимает одно значение из множества возможных значений.
Примеры.
1) Число очков, выпавших при однократном бросании игральной кости, есть случайная величина, она может принять одно из значений: 1, 2, 3, 4, 5, 6;
2) прирост веса домашнего животного за месяц есть случайная величина, которая может принять значение из некоторого числового промежутка;
3) число родившихся мальчиков среди пяти новорожденных есть случайная величина, которая может принять значения 0,1,2, 3, 4, 5.
Случайные величины будем обозначать прописными буквами X, Y, Z, а их возможные значения — соответствующими строчными буквами х, у, z. Например, если случайная величина X имеет три возможных значения, то они будут обозначены так: x1,x2,x3.
Случайная величина, принимающая различные значения, которые можно записать в виде конечной или бесконечной последовательности, называется дискретной случайной величиной.
Случайные величины из примеров 1 и 3 дискретные.
Случайная величина, которая может принимать все значения из некоторого числового промежутка, называется непрерывной случайной величиной.
Случайная величина из примера 2 является непрерывной.
В отличие от неслучайных (детерминированных) величин для случайной величины нельзя предсказать точно, какое она примет значение в определенных условиях, можно только указать закон распределения этой случайной величины.
Закон распределения случайной величины
Закон распределения считается заданным, если известны:
-
множество возможных значений случайной величины; -
способ количественного определения вероятности попадания случайной величины в произвольную область этого множества.