Файл: Учебнометодическое пособие знакомит студентов с основными понятиями о.doc

Пусть на плоскость бросают два тела, имеющие форму тетраэдра, грани которого занумерованы числами 1, 2, 3, 4. Допустим, что для каждого тетраэдра вероятность упасть на любую грань равна 1/4. В этом случае, если бросания тетраэдров выполняются независимо, то вероятность получить, например, результат (2,4), т. е. вероятность того, что первый тетраэдр упадет на грань 2, второй - на грань 4, равна (1/4)(1/4) = 1/16. Аналогично вычисляются и вероятности других исходов, так что каждый из 16 элементарных исходов имеет вероятность 1/16. На этом же пространстве элементарных исходов определим некоторую величину У, которая будет называться случайной величиной и значения которой у представляют собой суммы чисел, стоящих на нижних гранях тетраэдра.

(1,1)=2 (1,2)=3 (1,3)=4 (1,4)=5

(2,1)=3 (2,2)=4 (2,3)=5 (2,4)=6

(3,1)=4 (3,2)=5 (3,3)=6 (3,4)=7

(4,1)=5 (4,2)=6 (4,3)=7 (4,4)=8

Используя данные этой таблицы, легко получить распределение вероятностей f(y) случайной величины y.

Y	2	3	4	5		6	7	8
p(y)	1/16	2/16	3/16	4/16		3/16	2/16	1/16
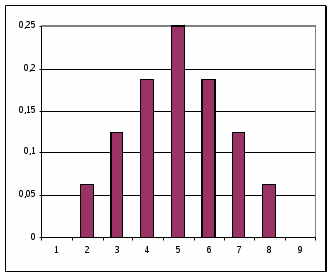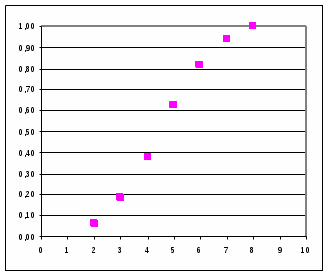Элементарные исходы и соответствующие значения y					График функции распределения

Функция F(x) = р(Х < х), определенная на множестве всех веще­ственных чисел х и задающая вероятность того, что случайная величина X не превзой­дет х, называется функцией распределения

Если X — случайная величина, то каково бы ни было вещественное число х, существует функция f(x) = р(Х = х), задающая вероятность того, что X принимает значение х. Эта функция определяет распределение частот и носит название плотности вероятности.

---

Функция распределения непрерывной случайной величины связана с плотностью вероятности следующим отношением:

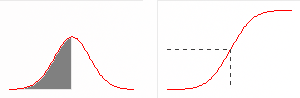Для дискретных случайных величин плотность распределения определяется набором вероятностей для отдельных дискретных значений в пространстве элементарных событий.
ТЕОРЕТИЧЕСКИЕ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ
При решении целого ряда теоретических и прикладных вопросов теории вероятностей и математической статистики возникает задача нахождения такого математического описания случайных величин, получаемых либо в ходе теоретических построений, либо при проведении экспериментов, с помощью которого они могут быть охарактеризованы посредством небольшого числа параметров. Этот подход состоит в попытке найти математическое выражение для так называемого теоретического распределения и выделить на основании аналитических выкладок и экспериментов параметры этого распределения таким образом, чтобы вся существенная информация, заключенная в анализируемых наборах случайных величин, сконцентрировалась в этих параметрах, а также в функциональной форме распределения.

Из большого числа теоретических распределений мы рассмотрим достаточно подробно в этом пособии только три, играющие важнейшую роль в теории вероятностей: биномиальное, пуассоновское и нормальное.
Биномиальное распределение
Повторные независимые испытания называются испытаниями Бернулли, если при каждом испытании имеется только два возможных исхода и вероятности этих исходов остаются неизменными для всех испытаний.

Пространство элементарных событий для каждого отдельного испытания состоит из двух точек, которые принято называть «успехом» (У) и «неудачей» (Н), а их вероятности обозначать соответственно через р и q, p+q=1. Для n испытаний Бернулли пространство элементарных событий содержит 2

---

ⁿ точек или последовательностей из n символов У и Н, где каждая точка представляет возможный исход составного опыта. Можно подсчитать вероятность появления какой-то определенной последовательности. Так как опыты независимы, то такая вероятность получается перемножением вероятностей элементарных событий У и Н, составляющих данную последовательность.

Рассмотрим следующий пример. Пусть пол новорожденного не зависит от пола детей, родившихся в семье до него. Примем для простоты, что соотношение полов 1 : 1, а это значит, что вероятности рождения мальчика или девочки одинаково равны ½. Если в семье двое детей, то можно оценить вероятность и того, что оба ребенка мальчики или девочки или один — мальчик, а другой — девочка. При принятом упрощении вероятности рождения двух мальчиков или двух девочек равны ½*½ =¼, а вероятности рождения сначала девочки, а потом мальчика и наоборот также равны ¼.

Усложним задачу. Пусть в семье пятеро детей и нас интересует вероятность того, что трое из них — мальчики, а двое — девочки, и при этом последовательность, в которой рождались эти дети, неважна. Тогда, исходя из тех же предположений, что и в предыдущем параграфе, вероятность рождения трех мальчиков будет равна (½)³, a девочек— (½)², а общая вероятность в семье с пятью детьми иметь трех мальчиков и двух девочек равна (½)³(½)²n₅, где n₅ —число различных последовательностей рождений трех мальчиков и двух девочек в рассматриваемой семье. Чему же равно это число? Очевидно, что оно равно числу сочетаний из пяти по два или по три т.е.



Таким образом, интересующая нас вероятность равна 5/16. Этот результат может быть записан в виде



Как в этой, так и в большом числе других задач представляет интерес лишь число успехов или неудач, достигнутых в последовательности из n испытаний Бернулли, независимо от порядка их следования. В общем случае, если производится серия из n зависимых испытаний, в каждом из которых возможны два исхода с вероятностями p и q=1-p, не меняющимися от испытания к испытанию, и при этом k раз имел место успех, а (n — k) раз — неудача (0 < k < n), то вероятность

Пусть в аудитории имеется 6 светильников и каждый из при включении может перегореть с вероятностью 1/4. Считается, что аудитория непригодна для занятий, если горят меньше чем четыре лампочки. Интерес представляет определение вероятности того, что после включения освещения аудитория будет непригодна для занятий.

---

Событие, означающее пригодность светильника при включении, обозначим через А. Тогда р(А) = 3/4, aq(A) = 1/4. Аудитория будет пригодна для занятий, если в ней будет гореть 4, 5 или 6 светильников. Вероятность сложного события, состоящего в том, что не менее 4 лампочек будет исправно, может быть подсчитана следующим образом:


Представим себе, что некоторое редкое заболевание встречается у 0,1% данной большой популяции. Из этой популяции случайно выбирают 5000 человек и проверяют на это заболевание. Интерес представляет определение того, каково наиболее вероятное число людей, имеющих это заболевание, и какова вероятность, что оно будет обнаружено именно у этого количества людей.

Условия задачи полностью соответствуют схеме Бернулли, поэтому наиболее вероятное число людей, у которых будет обнаружено заболевание при обследовании 5000 людей, равно n*р= 5000*0,001 = 5. Вероятность того, что именно у 5 человек будет найдено это заболевание, может быть найдена из распределения Бернулли:



Даже на непросвещенный взгляд вычисление интересующего нас результата таких параметрах получить довольно сложно. Мы отложим получение численного значения интересующей нас вероятности и перейдем к рассмотрению нового распределения, которое может быть представлено как приближение биномиального
Распределение Пуассона
Пусть в нашем распоряжении имеется биномиальная случайная величина с параметрами n и р, распределение вероятностей которой задается формулой биноминального распределения. Предположим, что n неограниченно увеличивается, а параметр р стремится к нулю таким образом, что произведение n*p=λ остается постоянным. Тогда,



Теперь вернемся к численной оценке вероятности обнаружения в случайной популяции из 5000 людей ровно пяти человек, страдающих неким заболеванием, встречающимся с частотой 0,001. Используя пуассоновское приближение биномиального распределения, имеем (λ=n*p=5):


Числовые характеристики дискретных случайных величин

---

Математическое значение дискретной случайной величины Х, имеющее конечное число возможных значений, равно

Дисперсия дискретной случайной величины Х, имеющее конечное число возможных значений, равно

или

Дискретная случайная величина задана рядом распределения:

Xi	1	2	4
Pi	0.1	0.3	0.6

M(X)=1*0.1+2*0.3+4*0.6=3.1

D(X)=(1-3.1)²*0.1+(2-3.1)²*0.3+(4-3.1)²*0.6=1.29

Или по второй формуле

D(X)=1²*0.1+2²*0.3+4²*0.6-3.1²=1.29

Нормальное распределение
В теории вероятностей и математической статистике важнейшую роль играет так называемое нормальное или гауссовское распределение. Значимость нормального распределения определяется тем, что оно служит хорошим приближением для большого числа наборов случайных величин, получаемых при наблюдениях и экспериментах. Нормальное распределение почти всегда имеет место, когда наблюдаемые случайные величины формируются под влиянием большого числа случайных факторов, ни один из которых существенно не превосходит остальные.

С другой стороны, нормальное распределение появляется как точное решение некоторых математических задач в рамках принятых моделей исследуемых явлений. Одно из первых таких решений, приводящие к нормальному закону распределения, были получены К. Гауссом при решении задач теории ошибок наблюдений и Дж. Максвеллом при учении распределения скоростей молекул в газе.

Функция 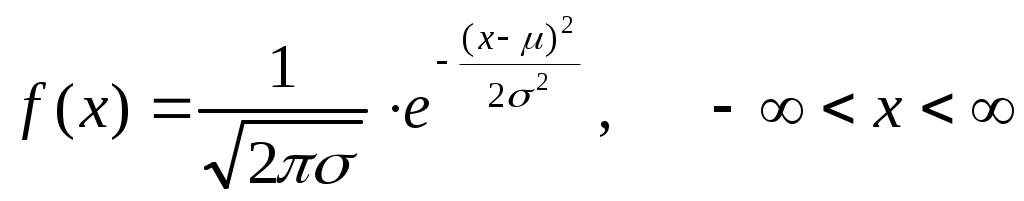носит название плотности нормального распределения, а ее интеграл 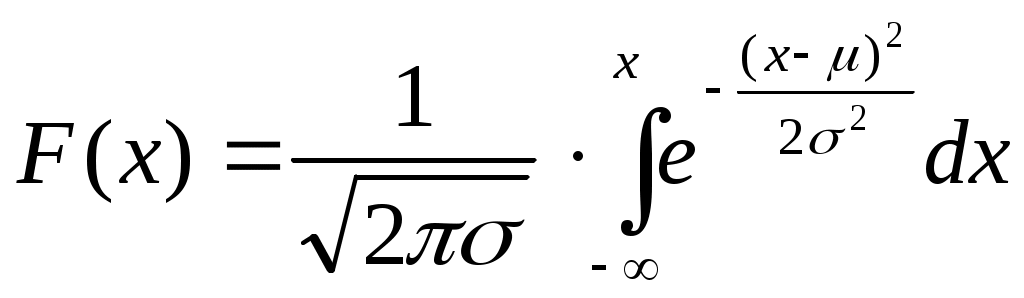называется нормальной функцией распределения.

Постоянная определена таким образом

---