Файл: Учебнометодическое пособие знакомит студентов с основными понятиями о.doc

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 12.12.2023

Просмотров: 471

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

ВВЕДЕНИЕУчебно-методическое пособие знакомит студентов с основными понятиями о теории вероятностей, случайных процессах, статистическом оценивании и проверке гипотез, статистических методах обработки экспериментальных данных, математических методах, принятых в биологических исследованиях.Пособие состоит из четырех разделов: Введение в теорию вероятностей. Основные понятия и термины статистики. Статистические методы обработки экспериментальных данных. Компьютерная обработка данных анализа в специализированной программе EasyStatistics. Введение в теорию вероятностей дает представление о случайных событиях, вероятности и ее свойствах, случайных величинах и основных теоретических распределениях случайных величин.При изучении второго раздела разбираются понятия о совокупности и выборке, классификации признаков, дается представление о схемах научного эксперимента и научных гипотезах, достоверности и надежности результатов.Третий раздел знакомит со статистическими методами описания групп, способами их сравнения в зависимости от характера распределения исходных данных. Большое внимание уделено корреляционно-регрессионному анализу, лежащему в основе многомерных методов анализа. Разбираются широко распространенные в биологических исследованиях методы оценки динамики, цикличности и классификации. При описании каждого метода описываются условия, необходимые для проведения статистической обработки, и возможные трудности в интерпретации полученных показателей. Четвертый раздел посвящен практическому применению методов статистической обработки данных с помощью специализированной программы «Статистическая обработка медико-биологических данных» (EasyStatistics). Данная программа разработана автором пособия (Роспатент №2003612171) и предназначена для статистической обработки данных биологических и медицинских исследований и, в первую очередь, нацелена на выполнение курсовых и дипломных работ студентами. В то же время это не замена уже существующим мощным статистическим пакетам, таким как Statistica, а скорее дополнение, помогающее оценить возможности манипулирования данными и принципы работы с основными статистическими методами. Каждый раздел содержит список вопросов и заданий для самопроверки.Пособие также содержит список учебно-методических материалов, рекомендуемых для самостоятельной работы студентов.РАЗДЕЛ I. ВВЕДЕНИЕ В ТЕОРИЮ ВЕРОЯТНОСТЕЙЗакономерности, которым подчиняются случайные события, изучаются в разделах математики, которые называются теорией вероятностей и математической статистикой.Понятие о случайном событииОпыт, эксперимент, на­блюдение явления называются испытанием. Испытаниями, напри­мер, являются: бросание монеты, выстрел из винтовки, бросание игральной кости (кубика с нанесенными на каждую грань числом очков — от одного до шести).Результат, исход испытания называется событием. Для обозначения событий используются большие буквы ла­тинского алфавита: А, В, С и т. д.Два события называются совместимыми, если появление одного из них не исключает появление другого в одном и том же испытании.Испытание: однократное бросание игральной кости. Событие А — появление четырех очков. Событие В— появле­ние четного числа очков. События Аи В совместимые.Два события называются несовместимы­ми, если появление одного из них исключает появление другого в одном и том же испытании.Испытание: однократное бросание монеты. Собы­тие А — выпадение герба, событие В — выпадение цифры. Эти события несовместимы, так как появление одного из них исключает появление другого.Несовместимость более чем двух событий означает их попарную несовместимостьИспытание: однократное бросание игральной кости. Пусть события А1, А2, А3, А4, А5, А6 соответственно выпа­дение одного очка, двух, трех и т. д. Эти события являются несов­местимыми..Два события А и В называются проти­воположными, если в данном испытании они несовместимы и одно из них обязательно происходит.Событие, противоположное событию А, обозначают через А.Испытание: бросание монеты. Событие А — выпадение герба, событие В — выпадение цифры. Эти события противоположны, так как исходами бросания могут быть лишь они, и появление одного из них исключает появление другого, т. е. А = В или А = В.Событие называется достоверным, если в данном испытании оно является единственно возможным его ис­ходом, и невозможным, если в данном испытании оно заведомо не может произойти.Испытание: извлечение шара из урны, в которой все шары белые. Событие А — вынут белый шар — достоверное событие; событие В — вынут черный шар — невозможное событие.Достоверное и невозможное события в данном испытании являются противоположными.Событие А называется случайным, если оно объективно может наступить или не наступить в данном испы­тании.Выпадение шести очков при броса­нии игральной кости — случайное событие. Оно может наступить, но может и не наступить в данном испытании.Прорастание девяноста восьми зерен пшеницы из ста — случайное событие. Это событие может наступить, но, может быть, прорастет зерен больше или меньше.Классическое определение вероятностиВсякое испыта­ние влечет за собой некоторую совокупность исходов — резуль­татов испытания, т. е. событий. Во многих случаях возможно пере­числить все события, которые могут быть исходами данного испы­тания.Говорят, что совокупность событий обра­зует полную группу событий для данного испытания, если его ре­зультатом обязательно становится хотя бы одно из них.События Ul, U2, ..., Un , образующие полную группу попарно несовместимых и равновозможных собы­тий, будем называть элементарными событиями.Вернемся к опыту с подбрасыванием игральной кости. Пусть Ui — событие, состоящее в том, что кость выпала гранью с цифрой i. Как уже отмечалось, события U1, U2, …, U6 образуют полную группу попарно несовместимых событий. Так как кость предполагается однородной и симметрич­ной, то события U1, U2, …, U6 являются и равновозможными, т. е. элементарными.Событие А называется благоприят­ствующим событию В, если наступление события А влечет за собой наступление события В.Пусть при бросании игральной кости события U2, U4 и U6 — появление соответственно двух, четырех и шести очков и А — событие, состоящее в появлении четного очка; собы­тия U2, U4 и U6 благоприятствуют событию А.Классическое определение вероятностиВероятностью Р (А) события А называется отношение m/n числа элементарных событий, благоприятствующих событию А, к числу всех элементарных событий, т. е. Вычислим вероятность выпадения герба при одном бросании монеты. Очевидно, событие А — выпадение герба и событие В — выпадение цифры — образуют полную группу несовместимых и равновозможных событий для данного испытания. Значит, здесь n = 2. Событию А благоприятствует лишь одно со­бытие — само А, т. е. здесь m = 1. Поэтому Р(А) = 0,5.Найти вероятность того, что при бросании иг­ральной кости выпадет число очков, делящееся на 2 (событие А). Число элементарных событий здесь 6. Число благоприятст­вующих элементарных событий 3 (выпадение 2, 4 и 6). Поэтому .Из приведенного классического определения вероятности вы­текают следующие ее свойства.1. Вероятность достоверного события равна единице.Действительно, достоверному событию должны благоприят­ствовать все n элементарных событий, т. е. m = n и, следовательно, P(A)=1.2. Вероятность невозможного события равна нулю. В самом деле, невозможному событию не может благоприят­ствовать ни одно из элементарных событий, т. е. m = 0, откуда P(A)=0.3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей.Действительно, случайному событию благоприятствует лишь часть из общего числа элементарных событий. Поэтому в этом случае 0 < m < n , значит, 0 <= Р (А)<= 1.Относительная частота.Статистическое определение ве­роятности.Классическое определение вероятности не являет­ся пригодным для изучения произвольных случайных событий. Так, оно неприемлемо, если результаты испытания не равновозможны. Например, при бросании неправильной игральной кости выпадение ее различных граней не равновозможно.В таких случаях используется так называемое статистическое определение вероятности.Пусть произведено n испытаний, при этом некоторое событие А наступило m раз. Число m называется абсолютной часто­той (или просто частотой) события А, а отношение называется относительной частотой события А.При транспортировке из 10 000 арбузов испор­тилось 26. Здесь m= 26 — абсолютная частота испорченных ар­бузов, а P*(A)=0,0026 относительная.Результаты многочисленных опытов и наблюдений помогают заключить: при проведении серий из n испытаний, когда число n сравнительно мало, относительная частота Р*(A) принимает зна­чения, которые могут довольно сильно отличаться друг от друга. Но с увеличением n — числа испытаний в сериях — относитель­ная частота Р*(А) приближается к некоторому числу Р(А), стабилизируясь возле него и принимая все более устойчивые значения.Было проведено 10 серий бросаний монеты, по 1000 бросаний в каждой. Относительные частоты выпадения герба оказались равными 0,501; 0,485; 0,509; 0,536; 0,485; 0,488; 0,500;0,497; 0,494; 0,484. Эти частоты группируются около числа 0,5Статистическое определение вероят­ностиВероятностью события А в данном испытании называется число Р (А), около которого группируются значения относительной частоты при больших n.По официальным данным шведской статистики, относительные частоты рождения девочек по месяцам 2007 г. харак­теризуются следующими числами (расположены в порядке сле­дования месяцев, начиная с января): 0,486; 0,489; 0,490; 0,471; 0,478; 0,482; 0,462; 0,484; 0,485; 0,491; 0,482; 0,473. Эти частоты группируются около числа 0,482.Таким образом, относительная частота события приближенно совпадает с его вероятностью, если число испытаний достаточно велико. Геометрическая вероятностьДо этого мы рассматривали возможные эксперименты, в которых реализуется конечное множество событий. Однако существует большое количество задач, для которых такое предположение не является справедливым. При решении таких задач предполагается, что множество реализуемых событий может быть представлено в виде некоторой геометрической фигуры, а конкретное событие соответствует точке заданной части этой фигуры. В качестве события A можно рассмотреть любую подобласть области Ω. Например, фигуру внутри исходной фигуры на плоскости или отрезок, лежащий внутри исходного отрезка на прямой.Заметим, что элементарным событием на таком множестве может быть только точка. В самом деле, если множество содержит более одной точки, его можно разбить на два непустых подмножества. Следовательно, такое множество уже неэлементарно.Теперь определим вероятность. Тут тоже все легко: вероятность «попадания» в каждую конкретную точку равна нулю. Иначе получим бесконечную сумму одинаковых положительных слагаемых (ведь элементарные события равновероятны), которые в сумме больше P(Ω) = 1.Итак, элементарные события для бесконечных областей Ω — это отдельные точки, причем вероятность «попадания» в любую из них равна нулю. Но как искать вероятность неэлементарного события, которое, подобно Ω, содержит бесконечное множество точек? Вот мы и пришли к определению геометрической вероятности.Геометрическая вероятность события A, являющегося подмножеством множества Ω точек на прямой или плоскости — это отношение площади фигуры A к площади всего множества Ω.Мишень имеет форму окружности. Какова вероятность попадания в ее правую половину, если попадание в любую точку мишени равновероятно? При этом промахи мимо мишени исключены. Взглянем на картинку: нас устроит любая точка из правого полукруга. Очевидно, площадь S(A) этого полукруга составляет ровно половину площади всего круга, поэтому имеем P=0,5Студент и студентка договариваются о встрече на заданном промежутке времени Т. Тот, кто приходит первым ожидает другого в течение времени tВ качестве множества элементарных событий рассмотри квадрат, состоящий из точек (x,y), 0<=x<=T, 0<=y<=T, где x и у время прихода его и ее.Благоприятсвующие события образуют точки, для которых |x-y|<t, т.е. точки квадрата между прямыми y=x-t, y=x+t. Площадь получающейся фигуры равна T2-(T-t)2, а площадь всего квадрата – Т2. Отсуда искомая вероятность Свойства вероятностейСложение вероятностей несовместимых событийСуммой событий А и В называется собы­тие С = А + В, состоящее в наступлении по крайней мере одного из событий А или В.Стрельба двух стрелков (каждый де­лает по одному выстрелу). Событие А — попадание в мишень пер­вым стрелком, событие В — попадание в мишень вторым стрелком. Суммой событий А и В будет событие С = А + В, состоящее в попадании в мишень по крайней мере одним стрелком.Произведением событий А и В назы­вается событие С = АВ, состоящее в том, что в результате испыта­ния произошло и событие А, и событие В.Аналогично произведением конечного числа событий A1 А2, …, Ak называется событие А = А1 * A2 * ... * Ak, состоящее в том, что в результате испытания произошли все указанные события.В условиях предыдущего примера произведением событий А и В будет событие С = АВ, состоящее в попадании в мишень двух стрелков.Из определения непосредственно следует, что АВ = ВА.Вероятность суммы двух несовместимых событий А и В равна сумме вероятностей этих событий:Р (А + В) = Р (А) + Р (В). Следствие. Сумма вероятностей противоположных собы­тий А и А равна единице:Р(А) + Р(А

Коэффициент сопряженности Чупрова. Дальнейшим обоб-щением четырехпольных таблиц являются многопольные таблицы, для которых сопряженность наиболее часто оценивается по формуле, предложенной русским статистиком А. А. Чупровым. Прежде чем приводить ее рассмотрим несколько реальных ситуаций, когда такая оценка может потребоваться. Известно, например, что окраска тюльпанов связана с наличием определенных пигментов. Может представлять интерес вопрос о том, с какими именно пигментами преимущественно связана та или иная окраска цветка. Или другой пример. Окружающая гнездо полярной крачки обстановка может представлять собой зеленые растения, растения и гальку, пестрые камешки и т. д. При этом можно наблюдать самые разные по качеству гнезда: от его отсутствия до очень хорошо сделанного. В этом случае желательно знать, связано ли качество гнезда с какой-то одной или несколькими характеристиками окружающей среды. Общим для этих и других подобных задач является то, что в распоряжении экспериментатора оказываются данные о некотором множестве объектов, обладающих двумя признаками, причем каждый из признаков может иметь несколько градаций. В этом случае , где m - число разновидностей явления Х; k - число разновидностей явления Y, n – общее число объектов (m*k). Независимо то того, что каждый из описательных признаков, несмотря на разницу в численности его разновидностей, можно свести к альтернативному - только с двумя разновидностями, довольно часто в практике возникает необходимость работать с описательными признаками более двух разновидностей. В таких случаях необходимо при вычислении коэффициента корреляции составлять так называемую корреляционную таблицу (где X1,X2,...Xn - обозначают разновидность одного признака, а Y1, Y2... Yn - разновидности другого).При наличии такой схемы коэффициент корреляции находят по формуле: , где - коэффициент связи, m- число разновидностей явления Х; k - число разновидностей явления Y.Данный метод пригоден также и для экспрессной оценки связи между количественными (например возраст) и качествен-ными (например брак) параметрами.На практике (особенно в зоологии и ботанике) довольно часто встречаются другие меры измерения связи.

, чтобы вероятность попадания в случайный интервал от -∞
Постоянные μ (математическое ожидание) и σ2 (дисперсия) называются параметрами распределения.



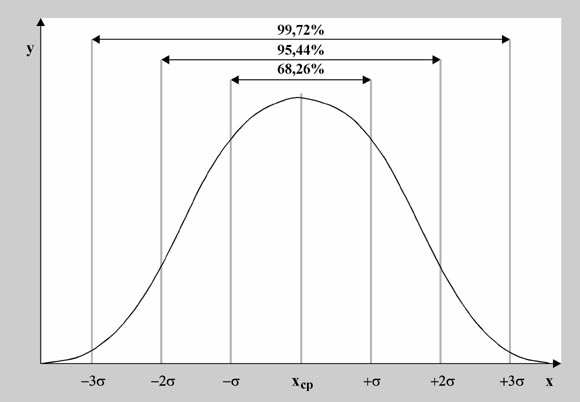
Общим для всех кривых нормального распределения является то, что примерно 68, 95 и 99,7 % площади под ними лежат соответственно в пределах ±σ, ±2σ, ±3σ.

Вопросы для самопроверки:


  1. Участники жеребьевки тянут из ящика жетоны с номерами от 1 до 100. Найти вероятность того, что номер первого наудачу извлеченного жетона не содержит цифры 5.

  2. При стрельбе по мишени вероятность сделать отличный вы­стрел равна 0,3, а вероятность выстрела на оценку «хорошо» рав­на 0,4. Какова вероятность получить за сделанный выстрел оценку не ниже «хорошо»?

  3. Вероятность того, что лицо умрет на 71-м году жизни, рав­на 0,04. Какова вероятность того, что человек не умрет на 71-м году?

  4. В урне 30 шаров: 15 белых, 10 красных и 5 синих. Какова вероятность вынуть цветной шар, если вынимается один шар?

  5. В урне 3 белых и 3 черных шара. Из урны дважды выни­мают по одному шару, не возвращая их обратно. Найти вероятность появления белого шара при втором испытании, если при первом испытании был извлечен черный шар.

  6. В колоде 36 карт. Наудачу вынимаются из колоды 2 кар­ты. Определить вероятность того, что вторым вынут туз, если первым тоже вынут туз.

  7. Пусть существует две лотереи: 5 из 36 и 31 из 36. Где вероятность выиграть больше?

  8. Два стрелка стреляют по цели. Вероятность поражения цели первым стрелком при одном выстреле равна 0,8, вторым стрел­ком — 0,7. Найти вероятность поражения цели двумя пулями в одном залпе.

  9. Студент М может заболеть гриппом (событие А) только в результате либо переохлаждения (событие В), либо контакта с другим больным (событие С). Требуется найти Р (А), если Р (В) = 0,5, Р (С) = 0,5, Рв (А) = 0,3, Рс (А) = 0,1 при условии не­совместимости В и С.

  10. Слово «керамит» составлено из букв разрезной азбуки. Затем карточки с буквами перемешиваются, и из них извлекаются по очереди четыре карточки. Какова вероятность, что эти четыре карточки в порядке выхода составят слово «река»?

  11. Вероятность получения желаемого результата в каждом опыте одинакова и равна 0,2. Опыты проводятся последовательно до получения желаемого результата. Определить вероятность того, что придется проводить пятый опыт.

  12. В ящике лежат 10 черных носков и 6 зеленых, все одного размера. Вы, не глядя, вытащили 3 носка, какова вероятность того, что образовалась хотя бы одна пара ?

13. Найти дисперсию и математическое ожидание дискретной случайной величины X, заданной законом распределения:

а)

X
4,3
5,1
10,6

p
0,2
0,3
0,5

б)

X
131
140
160
180

p
0,05
0,1
0,25
0,6

  1. В супе объемом 10л плавает 50 перчинок. С какой вероятностью в ложку объемом 0.01л попадет 1 перчинка.

  2. К случайной величине прибавили постоянную а. Как при этом изменятся ее а) математическое ожидание; б) дисперсия?

  3. Пусть вес пойманной рыбы подчиняется нормальному закону с параметрами: μ = 375 г, σ2= 25 г. Найти вероятность того, что вес пойманной рыбы будет от 300 до 425 г.

  4. Диаметр детали, изготовленной цехом, является случайной величиной, распределенной по нормальному закону. Дисперсия ее равна 0,0001, а математическое ожидание — 2,5 см. Найти границы, в которых с вероятностью 0,9973 заключен диаметр науда­чу взятой детали.

  5. Принимая вероятности рождения мальчика и девочки одина­ковыми, найти вероятность того, что среди 4 новорожденных 2 мальчика.

  6. Производится 10 независимых испытаний, в каждом из ко­торых вероятность появления события А равна 0,6. Найти диспер­сию случайной величины X — числа появлений события А в этих испытаниях.



РАЗДЕЛ II. ОСНОВНЫЕ ПОНЯТИЯ И ТЕРМИНЫ

БИОЛОГИЧЕСКОЙ СТАТИСТИКИ
Генеральная совокупность и выборка
Пусть требуется изучить множество однородных объектов (это множество называет­ся статистической совокупностью) относительно некоторого каче­ственного или количественного признака, характеризующего эти объекты. Например, если имеется партия деталей, то качественным признаком может служить стандартность детали, а количествен­ным — контролируемый размер детали.

Лучше всего произвести сплошное обследование, т. е. изучить каждый объект. Однако в большинстве случаев по разным причи­нам это сделать невозможно. Препятствовать сплошному обследо­ванию может большое число объектов, недоступность их. Если, на­пример, нужно знать среднюю глубину воронки при взрыве снаря­да из опытной партии, то, производя сплошное обследование, мы уничтожим всю партию.

Если сплошное обследование невозможно, то из всей совокуп­ности выбирают для изучения часть объектов.

Множество объектов, конечное или бесконечное, относительно которого делаются статистические выводы, носит название генеральной совокупности. Реально же мы имеем дело с конечными генеральными совокупностями, размеры которых, правда, могут колебаться в очень широких пределах.

Например, вся генеральная совокупность уссурийских тигров насчитывает около двухсот особей, в то время как число таких деревьев, как березы или осины, измеряется миллионами. В статистических выводах важен не сам по себе объем генеральной совокупности, а та доля от него, которую составляет выборка. Во всех случаях, когда объем выборки меньше сотой части всей генеральной совокупности, последнюю по отношению к выборке принято считать практически бесконечной и использовать математический аппарат, основанный на таком представлении.

Множество объектов, случайно отобранных из генеральной совокупности, называется выборкой.

Плоды одного дерева (200 штук) обследуют на на­личие специфического для данного сорта вкуса. Для этого отби­рают 10 шт. Здесь 200 — объем генеральной совокупности, а 10 — объем выборки.

Число объектов генеральной совокупности и выборки называ­ется соответственно объемом генеральной совокупности и объемом выборки.

Если выборку отбирают по одному объекту, который обследу­ют, и снова возвращают в генеральную совокупность, то выборка называется повторной. Если объекты выборки уже не возвращаются в генеральную совокупность, то выборка называется бесповторной. На практике чаще используется бесповторная выборка. Если объем выборки составляет небольшую долю объема генеральной совокупности, то разница между повторной и бесповторной незначительна.


Непреднамеренный отбор. Метод последовательных номеров.

Случайный и механический методы отбора

Особенностью биологических исследований является то, что подопытный материал, находящийся в распоряжении исследователя, поступает к нему случайно. Поэтому не всегда удается соблюсти метод случайного отбора. Пренебрежение методами случайного отбора приводит к тому, что результаты одинаковых исследований различны у различных исследователей.

Можно опять применить случайный отбор по таблице случайных чисел. Кроме этого существует метод, называемый механическим (Россия) или систематическим (США, Англия). Сущность этого метода в следующем: делят общее число случаев на число случаев, за которыми надо наблюдать, и получают так называемую интервальную стопу. Затем по таблице находят первое число и 5, 10, 15, 20.

Признаки и показатели
ПРИЗНАКОМ в статистике называют свойство, характерную черту или иную особенность единиц совокупности, которые могут быть наблюдаемы и измерены. Признаки, принимающие различные значения или видоизменения у отдельных единиц совокупности, называются варьирующими, а отдельные их значения или видоизменения - вариантами.

В литературе приняты различные принципы клас­сификации признаков по шкалам измерений. Классификация в за­висимости от числа допустимых арифметических операций над признаками, измеренными в данных шкалах, включает:
Номинальные признаки (признаки с неупорядоченными состо­яниями, классификационные признаки), например: велосипед, мотоцикл, автомобиль. Номинальные признаки могут быть оциф­рованы — 0,1,2, однако смысла эти цифры, за исключением воз­можности различать признаки между собой, не имеют. Частным случаем номинальных признаков являются бинарные (каче­ственные, дихотомические) признаки, представляющие собой но­минальные признаки с двумя градациями, например: «нет» — 0, «да» — 1. Рекомендуется для бинарных признаков использо­вать оцифровку типа 0 и 1, а не какую-либо иную (например, -1 и +1), так как только эти две цифры предполагается исполь­зовать в методах анализа бинарных признаков.
Порядковые признаки (признаки с упорядоченными состояния­ми, ординальные признаки), например: отлично, хорошо, удов­летворительно, плохо. Порядок состояний имеет смысл, призна­ки могут быть осмысленно оцифрованы (в данном примере: 5, 4, 3, 2) и могут сравниваться между собой, однако расстояния между ними не определены. Как и предыдущие, подобного типа признаки часто используются в задачах диагностики, в том числе медицинской.

Количественные (численные, вариационные) признаки, иногда подразделяемые на интервальные и относительные, различаю­щиеся положением нулевой отметки на шкале измерения. На­пример, год рождения — относительный количественный признак, а срок службы в рядах вооруженных сил — интервальный коли­чественный признак. Если в первом примере определены только операции различения, сравнения и вычитания, то во втором к ним добавляются операции сложения и отношения. Числен­ные признаки определяют измеряемые или исчислимые количе­ства (величины) и являются истинными количественными, при­чем могут измеряться как непрерывные, так и целочисленные признаки.
Действия над признаками, измеренными в различных шкалах

Шкала измерения
Допустимые действия
Пример применения

Номинальная
Различение
Наличие или отсутствие симптома

Порядковая
Различение, сравнение
Школьная оценка

Количественная
Различение, сравнение, все арифметические операции
Температура, масса, время, длина


Шкалы могут приводиться одна к другой: количественная шкала — к порядковой или номинальной, порядковая шкала — к номиналь­ной. Обратные операции считаются некорректными. Приведение одной шкалы к другой обычно называют понижением шкалы. При­ведение признаков к шкале, отличной от тех, в которых первоначально признаки были измерены, необходимо при анализе групп призна­ков, измеренных в разных шкалах. Понижение шкалы ведет к потере некоторой части информации об изучаемых признаках.
Правила ранжирования
Использование порядковой шкалы позволяет присваивать ранги объектам по какому-либо признаку. Таким образом, метрические значения переводятся в ранговые. При этом фиксируются различия в степени выраженности свойств. В процессе ранжирования следует придерживаться 2 правил.

Правило порядка ранжирования. Надо решить, кто получает первый ранг: объект с самой большей степенью выраженности какого-либо качества или наоборот. Чаще всего это абсолютно безразлично и не отражается на конечном результате. Традиционно принято первый ранг приписывать объектам с большей степенью выраженности качества (большему значению – меньший ранг). Например, чемпиону присуждают первое место, а не наоборот. Хотя, и здесь если бы был принят обратный порядок, то результаты от этого не изменились бы. Так что порядок ранжирования каждый исследователь вправе определять сам. Например, Е.В. Сидоренко рекомендует меньшему значению приписывать меньший ранг. В некоторых случаях это удобнее, но непривычнее.

Смотрите также файлы