ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 1132
Скачиваний: 29
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
до того момента, когда количество больных станет равно нулю.
Уровень A.
Ответ:
Ответ:
через 39 дней
Ответ:
980 переболеют
20 не заболеют
Ответ:
648
Уровень B.
Ответ:
при K 1,1
Уровень C.
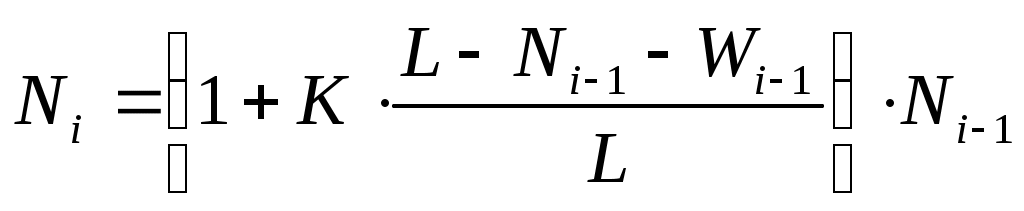 ,
, 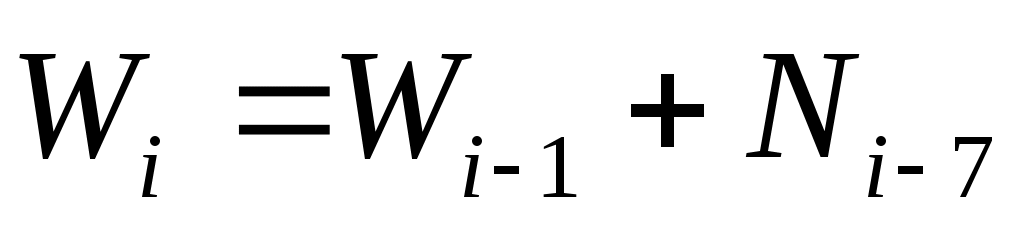 .
.
Постройте график изменений количества больных этой и предыдущей моделей на одном поле:
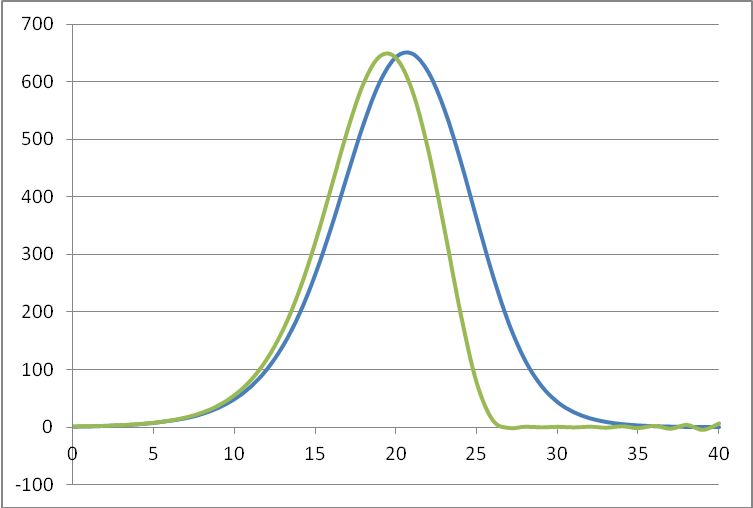
Анализируя результаты моделирования, докажите, что эта модель неадекватна.
Ответ:
отрицательное число больных при i 27
количество выздоровевших больше количества жителей при i 22
Какие допущения, на ваш взгляд, были сделаны неверно при разработке этой модели?
Ответ:
формула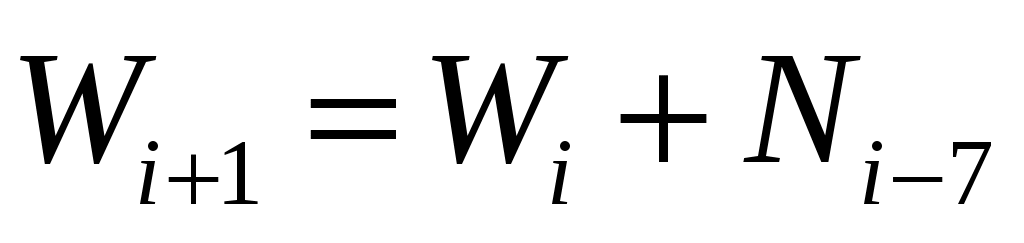 учитывает человека как выздоровевшего несколько раз (все дни, которые он болел)
учитывает человека как выздоровевшего несколько раз (все дни, которые он болел)
Сравните поведение двух моделей при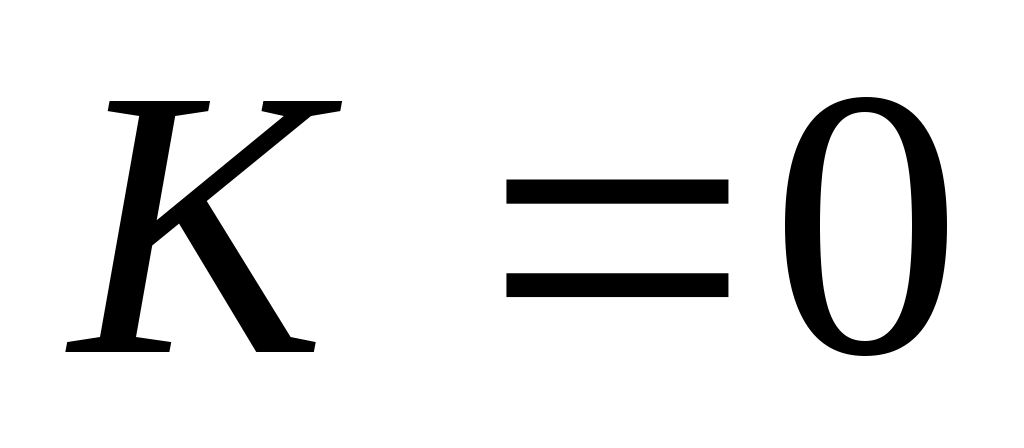 ,
, 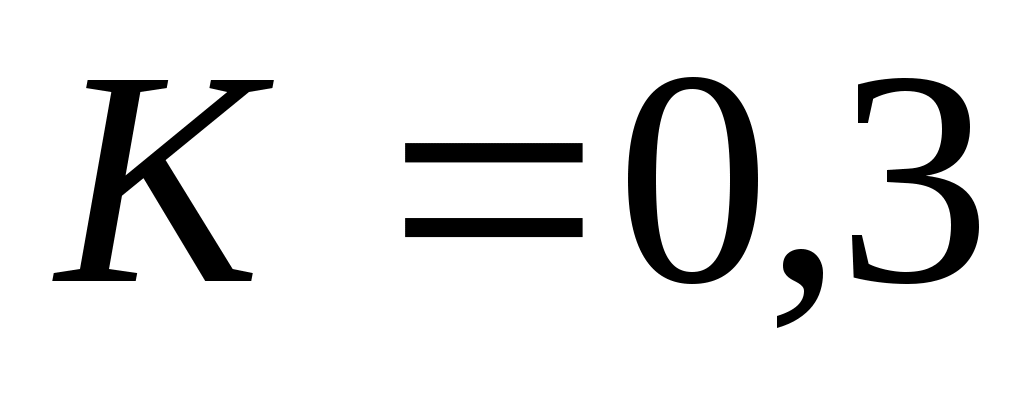 и
и 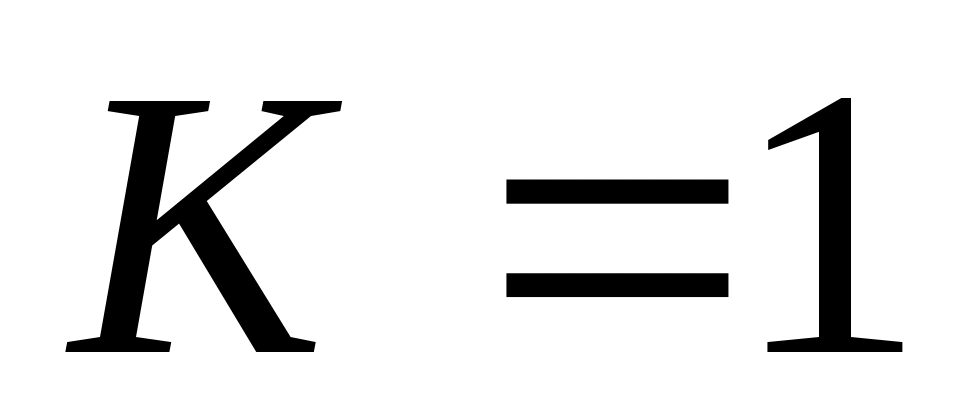 . Сделайте выводы.
. Сделайте выводы.
Ответ:
K = 0 результаты совпадают
K = 0,3 вторая модель неадекватна, количество выздоровевших более 4000
K = 1 вторая модель дает нереально большие положительные и отрицательные значения N и W
Для выполнения работы откройте файл-заготовку ХищникЖертва.xls.
Выполните моделирование биологической системы «щуки-караси»
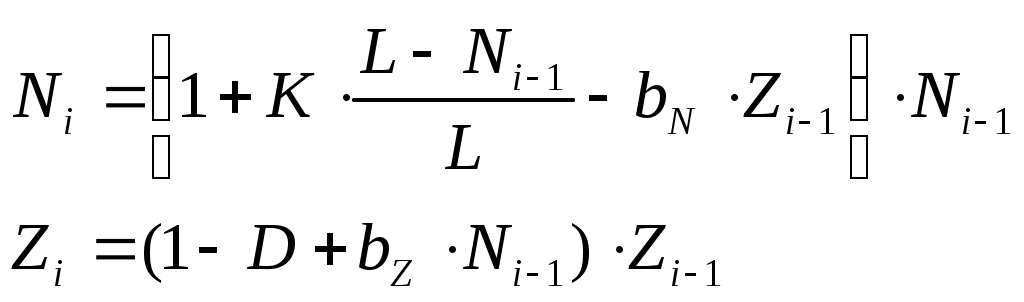
где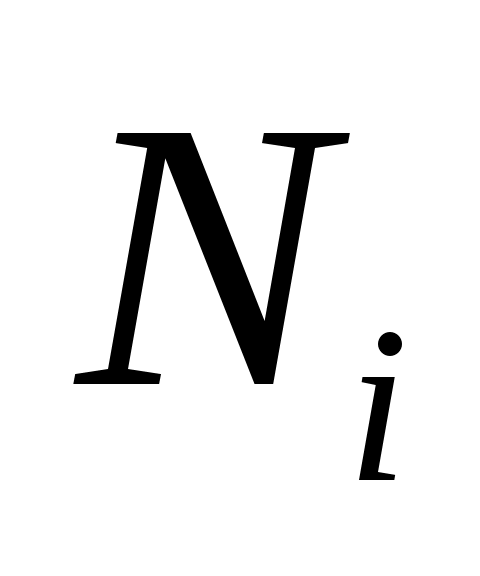 – численность карасей
– численность карасей
 – численность щук
– численность щук
при следующих значениях параметров:
 – коэффициент прироста карасей;
– коэффициент прироста карасей;
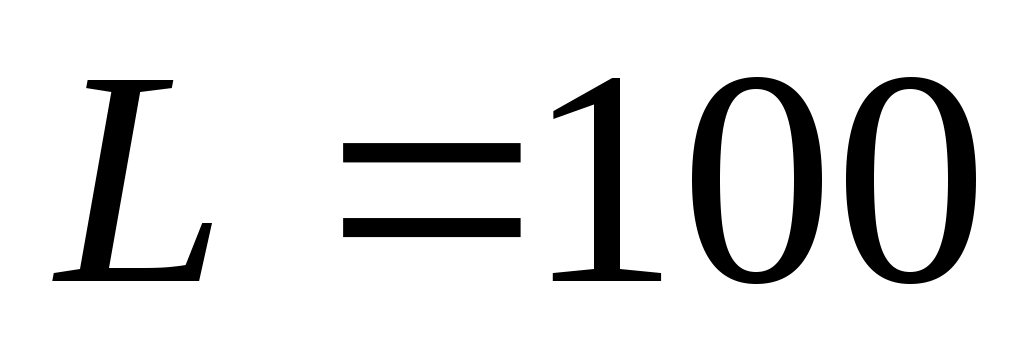 – предельная численность карасей;
– предельная численность карасей;
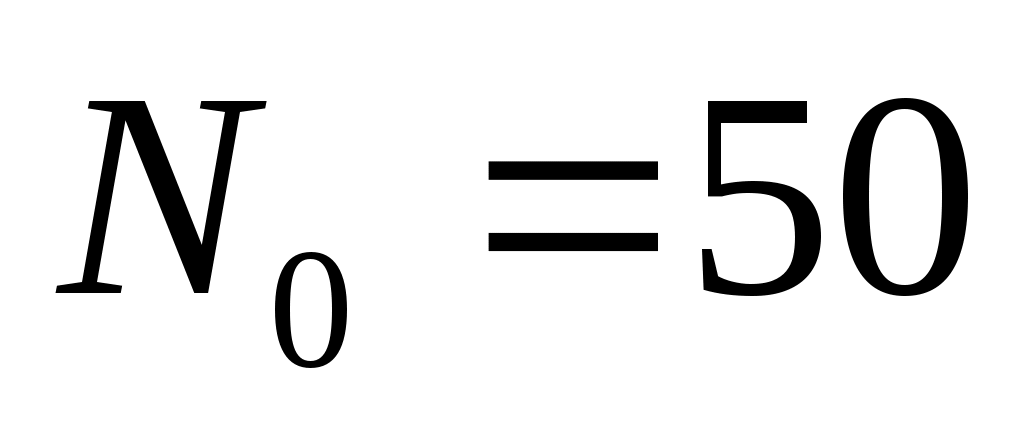 – начальная численность карасей;
– начальная численность карасей;
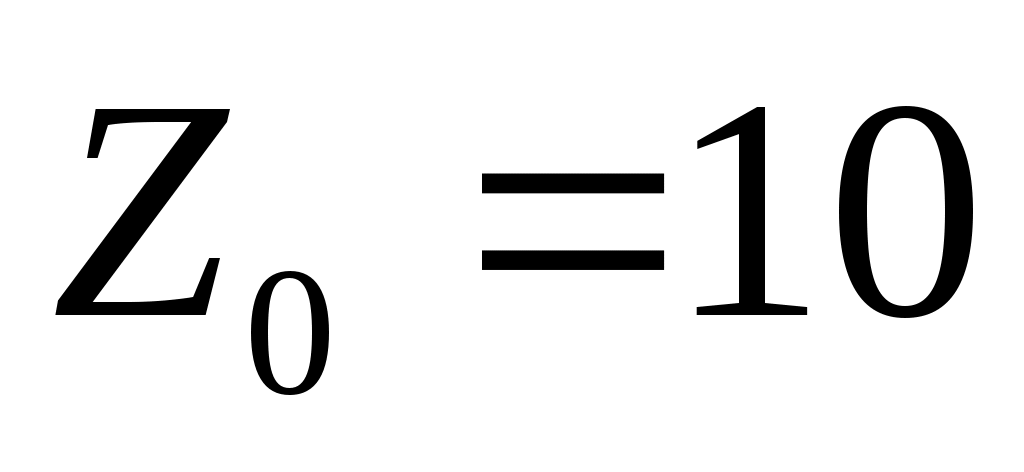 – начальная численность щук;
– начальная численность щук;
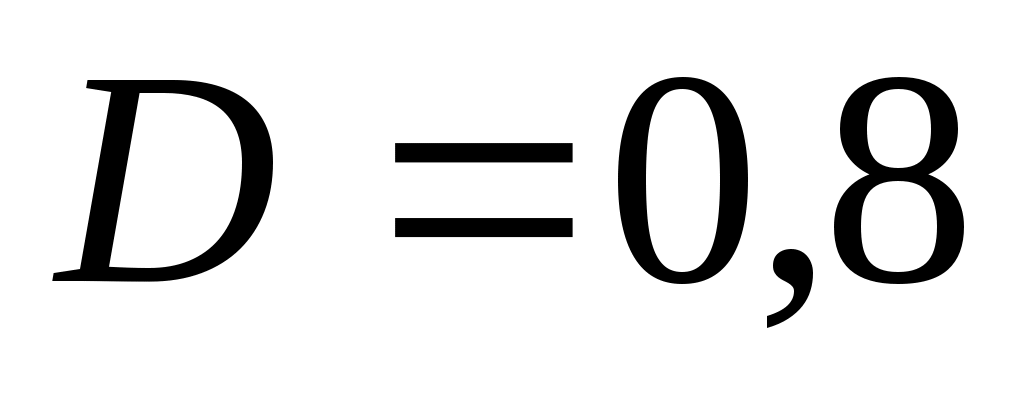 – коэффициент смертности щук без пищи;
– коэффициент смертности щук без пищи;
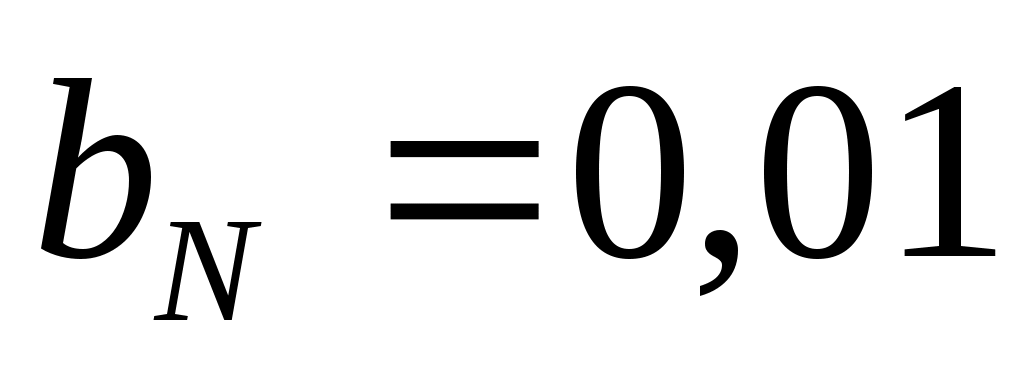 и
и 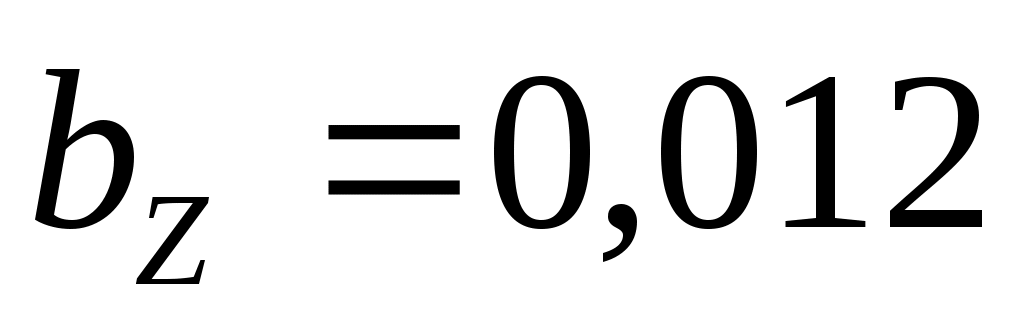 – коэффициенты модели.
– коэффициенты модели.
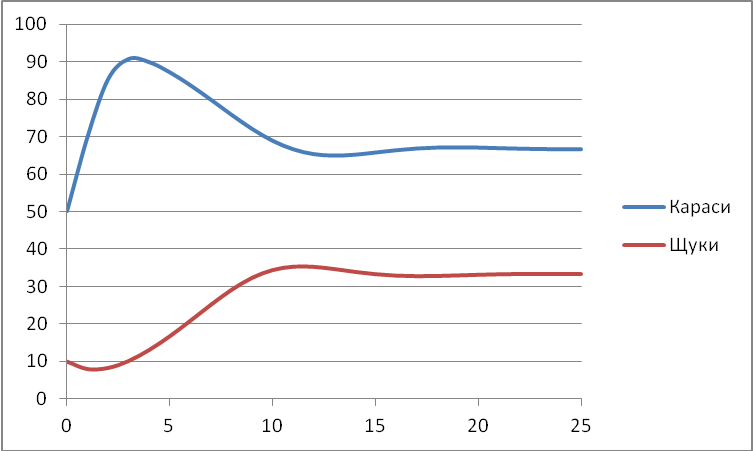
Постройте на одном поле графики изменения численности карасей и щук в течение 30 периодов моделирования.
Уровень A.
Ответ:
Ответ:
66 карасей
33 щуки
Ответ:
значения коэффициентов
Уровень B.
Ответ:
на начальную часть графиков до установления равновесия
Ответ:
при bZ=0,1 появляются отрицательные значения
Уровень C.
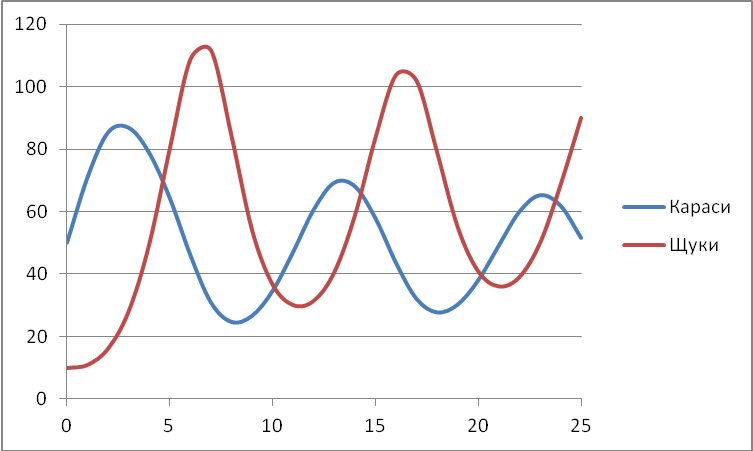
Как вы можете объяснить это с точки зрения биологии?
Ответ:
Количество карасей растет, растет кормовая база щук и их количество увеличивается. Затем карасей становится меньше, щукам уже не хватает еды, они начинают вымирать. И т.д. по циклу.
Ответ:
bZ = 0,007
Как вы можете объяснить это с точки зрения биологии?
Ответ:
Щуки не наедаются теми карасями, которых они способны поймать.
Для выполнения работы откройте файл-заготовку ДвеПопуляции.xls.
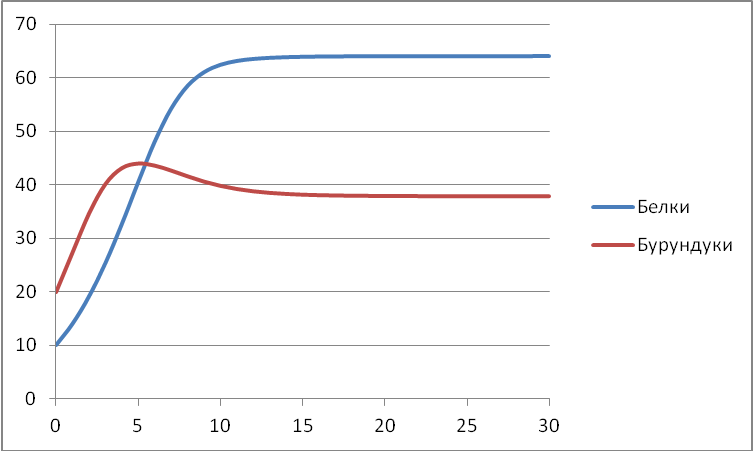
Белки и бурундуки живут в одном лесу и едят примерно одно и то же (конкурируют за пищу). Модель, описывающая изменение численности двух популяций, имеет вид:
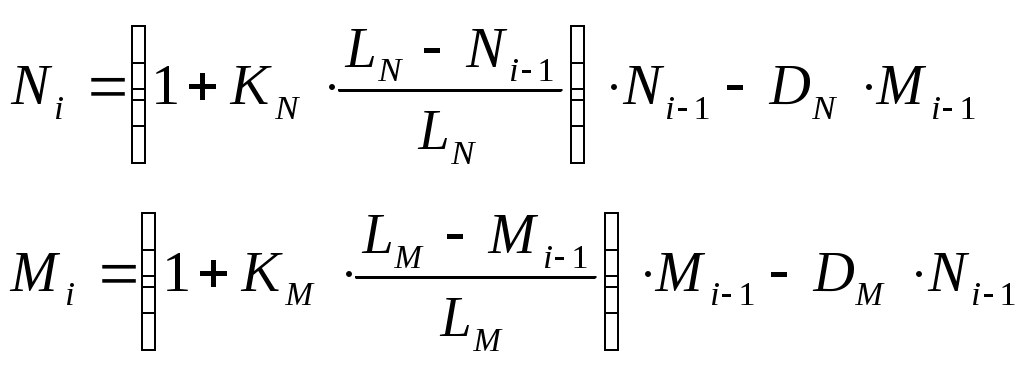
Здесь и
и 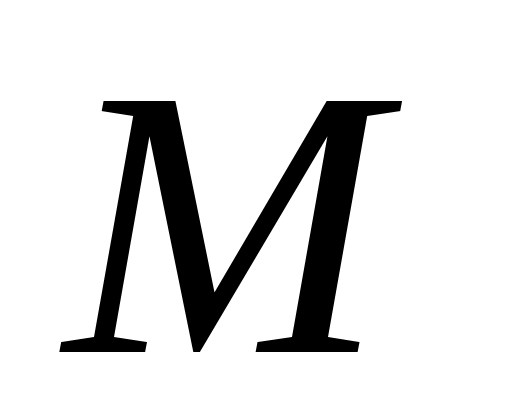 – численность белок и бурундуков;
– численность белок и бурундуков; 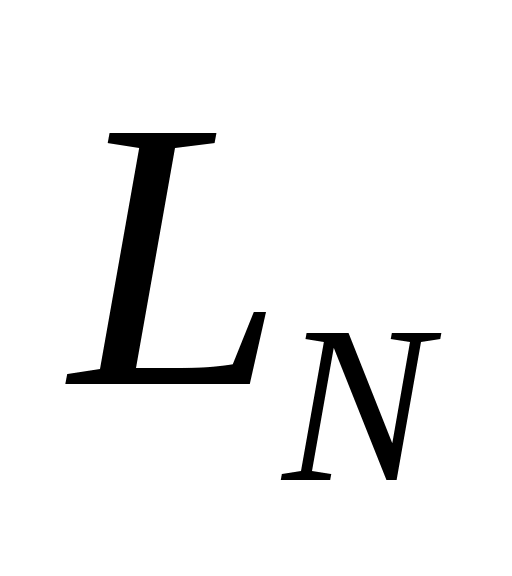 и
и 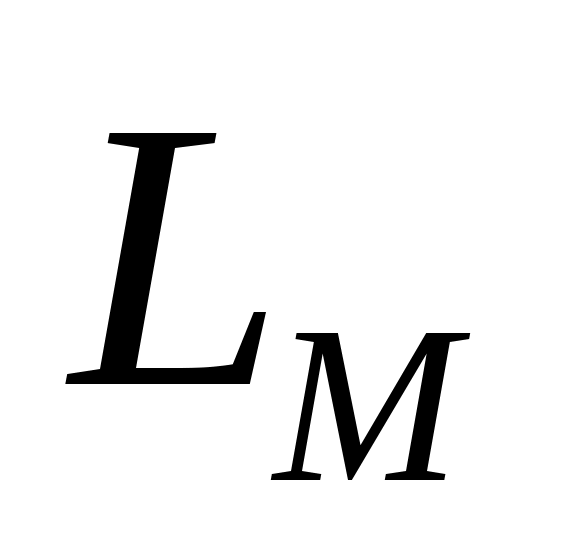 – их максимальные численности;
– их максимальные численности; 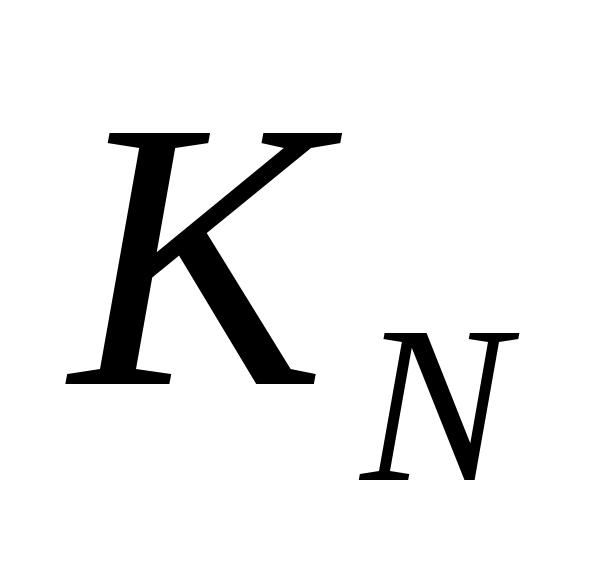 и
и 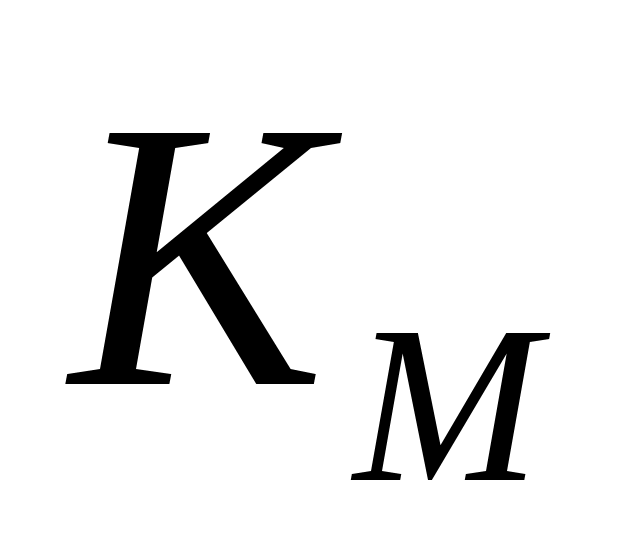 – коэффициенты прироста;
– коэффициенты прироста; 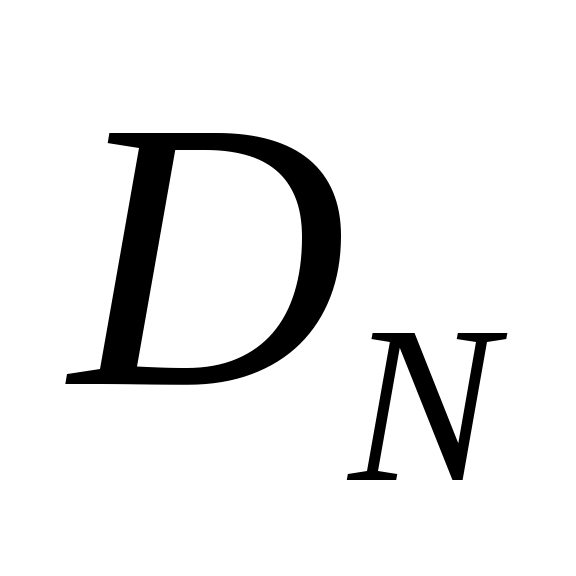 и
и 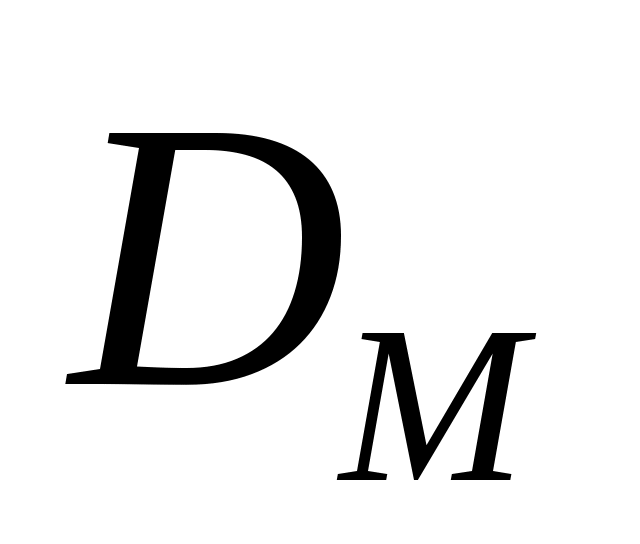 – коэффициенты взаимного влияния.
– коэффициенты взаимного влияния.
Объясните, на основании каких предположений была построена эта модель.
Ответ:
Увеличение численности другого виду уменьшает количество корма и поэтому снижает численность животных данного вида.
Выполните моделирование изменения численности двух популяций в течение 30 периодов при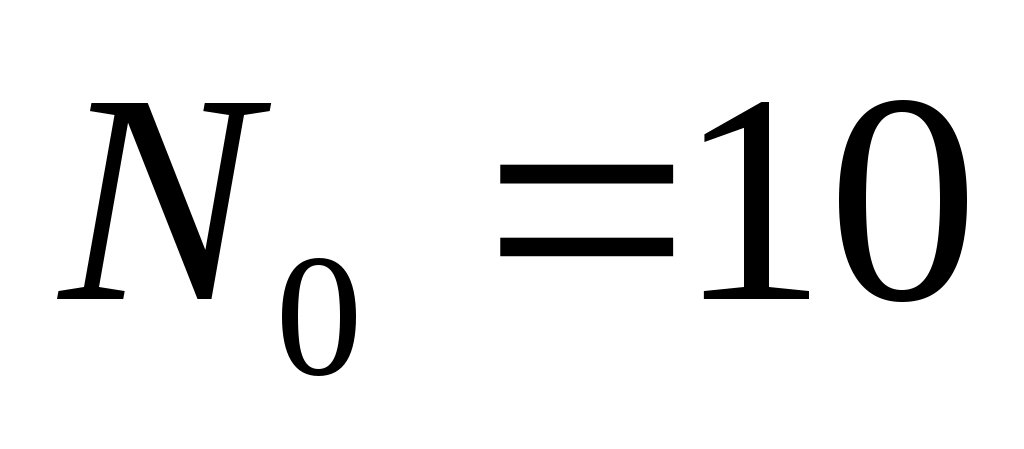 ,
, 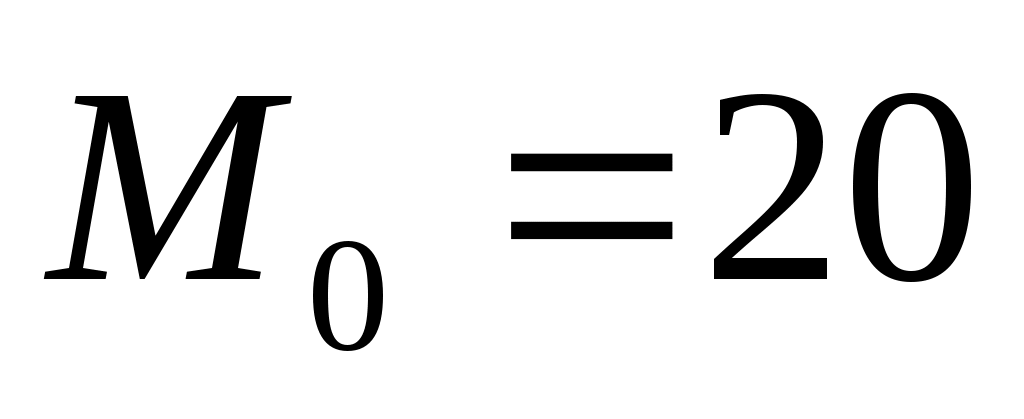 ,
, 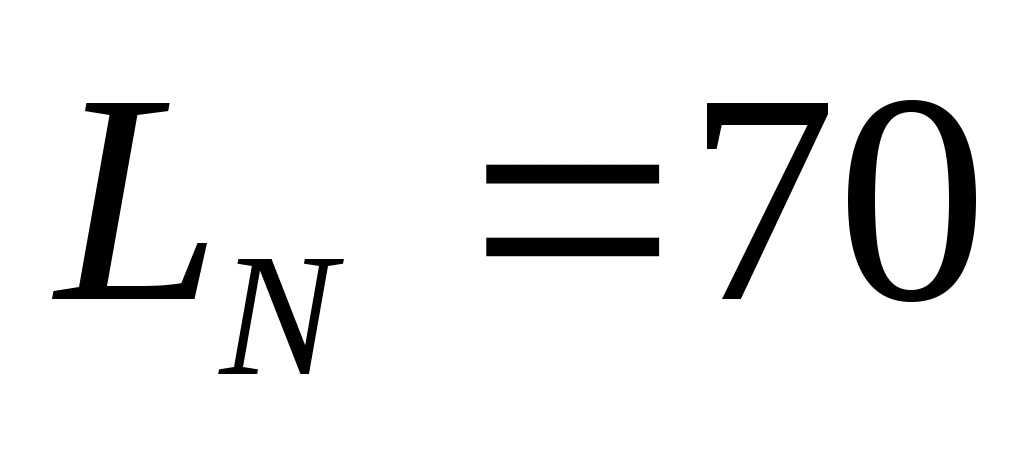 ,
, 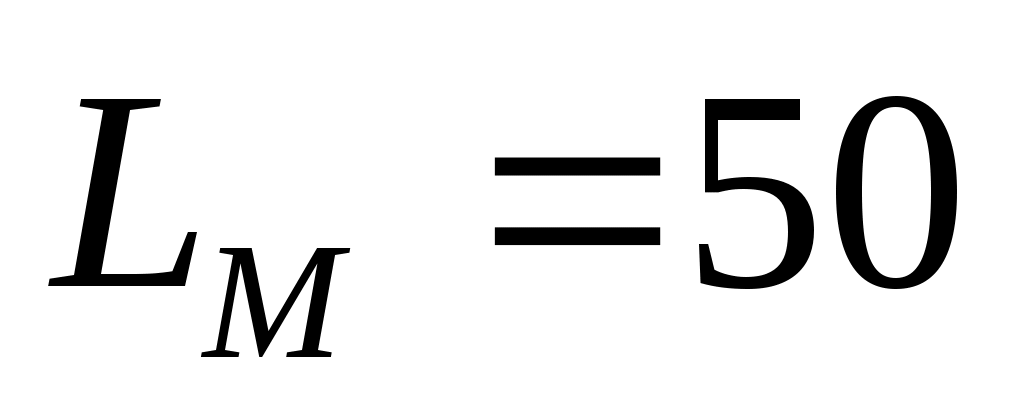 ,
, 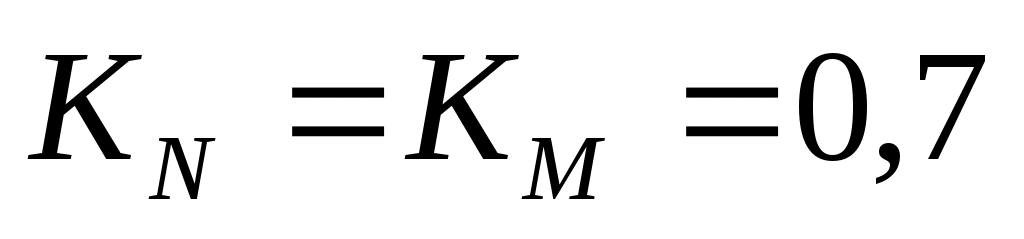 и
и 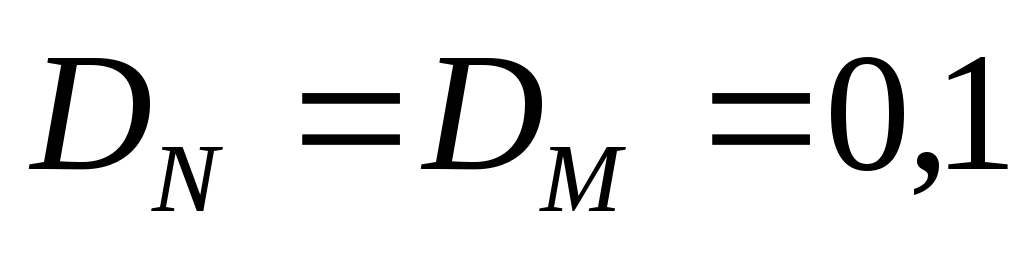 .
.
Уровень A.
Ответ:
Да, она учитывает влияние одной популяции на другую.
Уровень A.
-
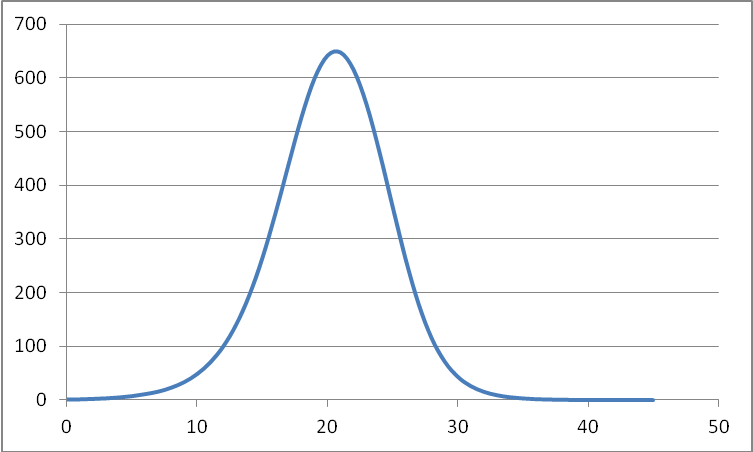
Постройте график изменения количества больных в течение 40 дней.
Ответ:

-
Когда закончится эпидемия?
Ответ:
через 39 дней
-
Сколько человек переболеет, а сколько вообще не заболеет гриппом?
Ответ:
980 переболеют
20 не заболеют
-
Каково максимальное число больных в один день?
Ответ:
648
Уровень B.
-
Изменяя коэффициент с шагом 0,1, определите, при каких значениях
с шагом 0,1, определите, при каких значениях  модель явно перестает быть адекватной.
модель явно перестает быть адекватной.
Ответ:
при K 1,1
Уровень C.
-
*Сравните модель, использованную в этой работе, со следующей моделью:
Постройте график изменений количества больных этой и предыдущей моделей на одном поле:

Анализируя результаты моделирования, докажите, что эта модель неадекватна.
Ответ:
отрицательное число больных при i 27
количество выздоровевших больше количества жителей при i 22
Какие допущения, на ваш взгляд, были сделаны неверно при разработке этой модели?
Ответ:
формула
Сравните поведение двух моделей при
Ответ:
K = 0 результаты совпадают
K = 0,3 вторая модель неадекватна, количество выздоровевших более 4000
K = 1 вторая модель дает нереально большие положительные и отрицательные значения N и W
- 1 2 3 4 5 6
Модель «хищник-жертва»
Для выполнения работы откройте файл-заготовку ХищникЖертва.xls.
Выполните моделирование биологической системы «щуки-караси»
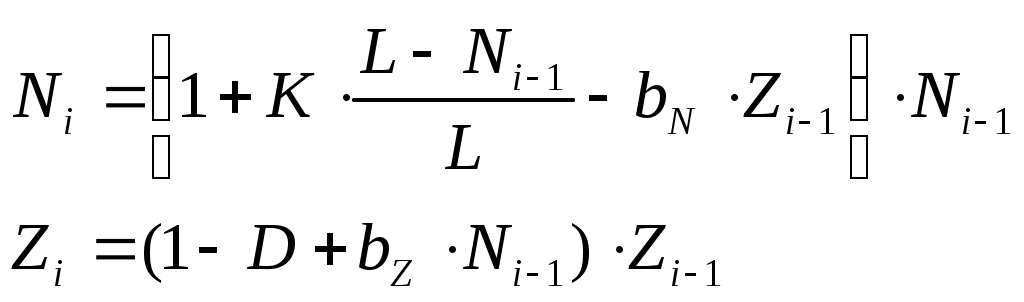
где
при следующих значениях параметров:
Постройте на одном поле графики изменения численности карасей и щук в течение 30 периодов моделирования.
Уровень A.
-
Выполните моделирование двух популяций в течение 25 периодов. Постройте графики изменения численности карасей и щук.
Ответ:

-
Сколько карасей и щук живут в водоеме в состоянии равновесия?
Ответ:
66 карасей
33 щуки
-
Выясните, что влияет на количество рыб в состоянии равновесия: начальная численность хищников и жертв или значения коэффициентов модели?
Ответ:
значения коэффициентов
Уровень B.
-
На что влияет начальная численность хищников и жертв?
Ответ:
на начальную часть графиков до установления равновесия
-
Подберите значения коэффициентов, при которых модель становится неадекватна. Объясните, почему вы считаете, что она неадекватна.
Ответ:
при bZ=0,1 появляются отрицательные значения
Уровень C.
-
Установите значения коэффициентов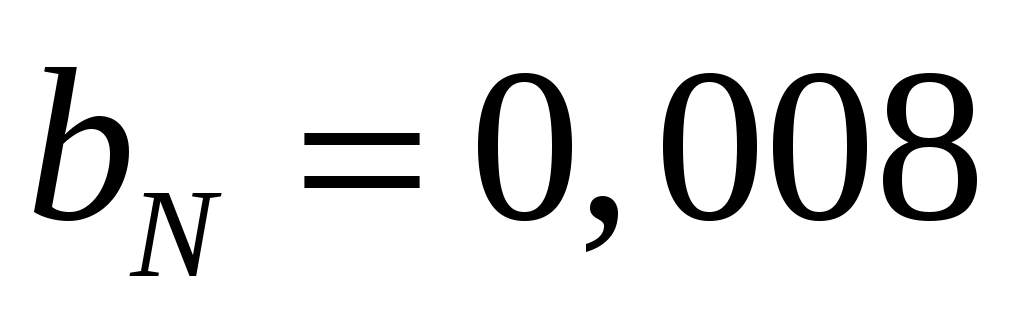 и
и 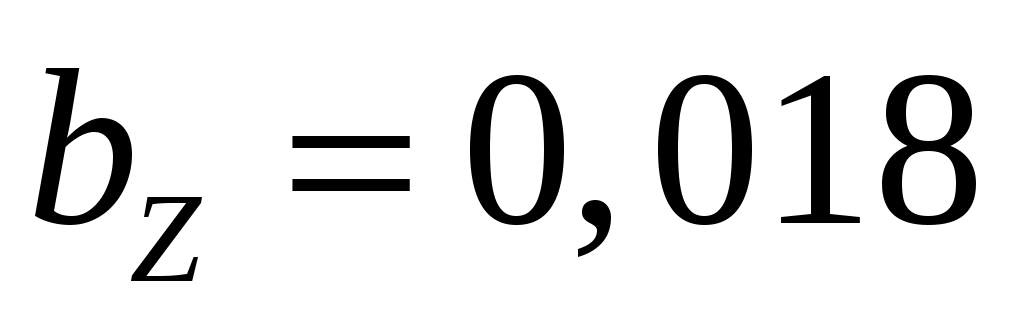 . Вставьте в отчёт график, который вы увидели:
. Вставьте в отчёт график, который вы увидели:

Как вы можете объяснить это с точки зрения биологии?
Ответ:
Количество карасей растет, растет кормовая база щук и их количество увеличивается. Затем карасей становится меньше, щукам уже не хватает еды, они начинают вымирать. И т.д. по циклу.
-
Установите значения коэффициента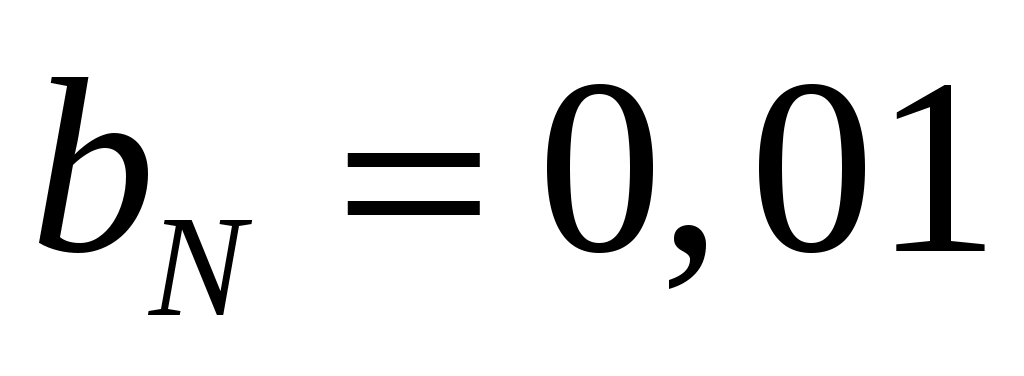 . Найдите экспериментально наибольшее значения коэффициента bZ (с точностью 0,001), при котором к 25 году щуки вымирают, а численность карасей достигает предельно возможного значения.
. Найдите экспериментально наибольшее значения коэффициента bZ (с точностью 0,001), при котором к 25 году щуки вымирают, а численность карасей достигает предельно возможного значения.
Ответ:
bZ = 0,007
Как вы можете объяснить это с точки зрения биологии?
Ответ:
Щуки не наедаются теми карасями, которых они способны поймать.
Практическая работа № 11а.
Модель «две популяции»
Для выполнения работы откройте файл-заготовку ДвеПопуляции.xls.
Белки и бурундуки живут в одном лесу и едят примерно одно и то же (конкурируют за пищу). Модель, описывающая изменение численности двух популяций, имеет вид:
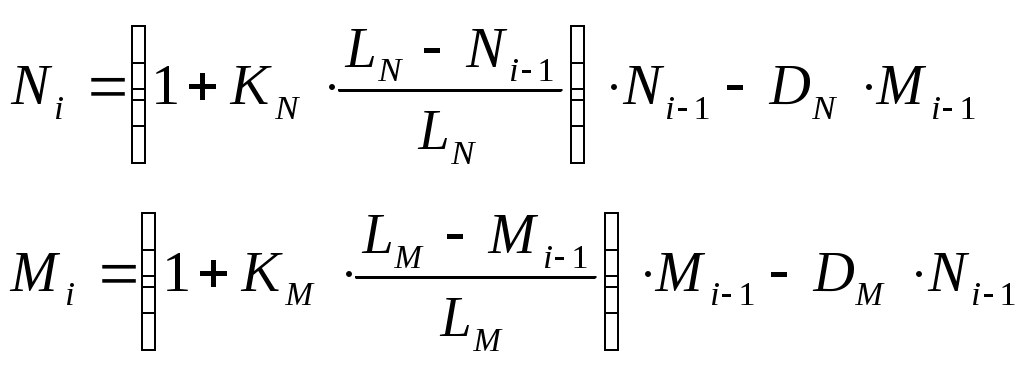
Здесь
Объясните, на основании каких предположений была построена эта модель.
Ответ:
Увеличение численности другого виду уменьшает количество корма и поэтому снижает численность животных данного вида.
Выполните моделирование изменения численности двух популяций в течение 30 периодов при
Уровень A.
-
Постройте графики изменения численности обеих популяций на одном поле.

-
Является ли эта модель системной? Почему?
Ответ:
Да, она учитывает влияние одной популяции на другую.