ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 1130
Скачиваний: 29
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Уровень B.
-
Напишите программу, которая моделирует полет мяча, брошенного вертикально вверх, при
Остальные необходимые данные есть в тексте § 10. Выполните следующие задания:
-
определите время полета, максимальную высоту подъема мяча и скорость в момент приземления; -
вычислите время полета и максимальную высоту подъема мяча, используя модель движения без сопротивления воздуха:
-
сравните эти результаты с полученными при моделировании с учетом сопротивления;
без учёта
сопротивления
с учётом
сопротивления
ошибка (%)
Время полета, с
4,07
3,90
4,4%
Максимальная высота, м
20,39
18,23
11,8%
Скорость приземления, м/с
20
18,45
8,4%
-
можно ли в этой задаче пренебречь сопротивлением воздуха? почему?
Ответ:
нельзя, без учета силы сопротивления результаты имеют значительную ошибку (по высоте – более 10%)
-
с помощью табличного процессора постройте графики изменения скорости, ускорения и силы сопротивления (указание: из программы сохраните данные в CSV-файл, разделив данные в каждой строке точками с запятой):
Скорость:
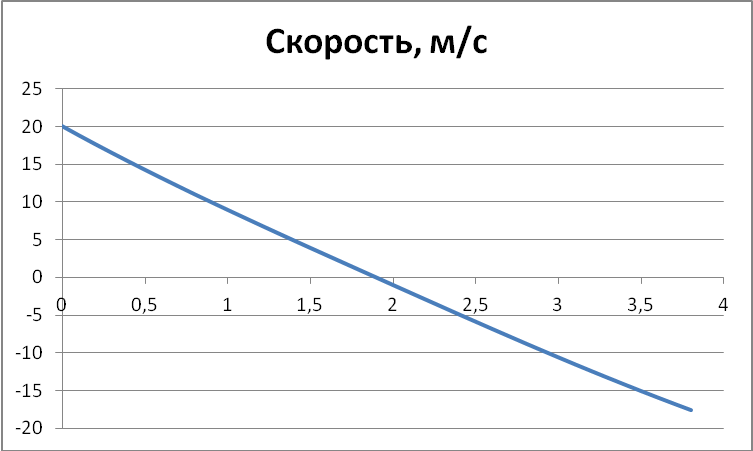
Ускорение:
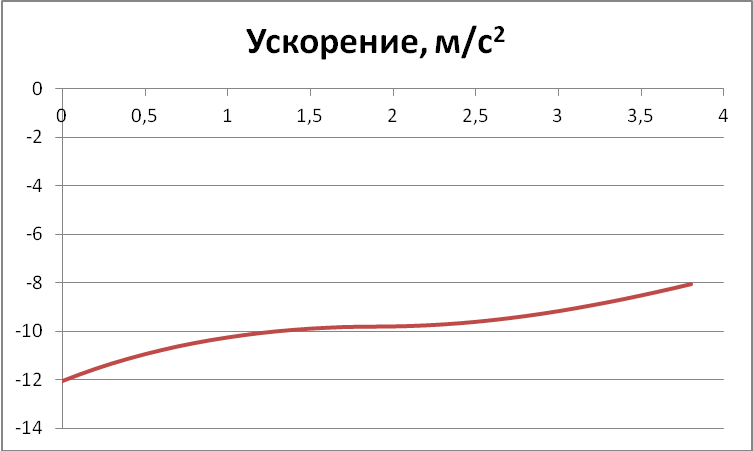
Сила сопротивления:
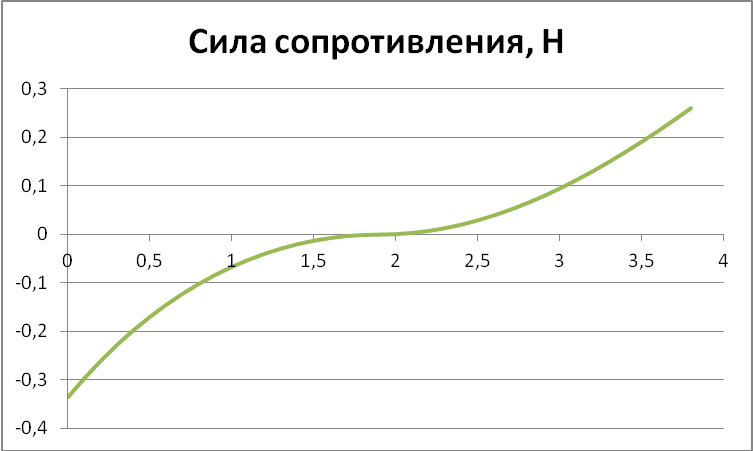
-
уменьшите шаг сначала до 0,01 с и повторите моделирование; затем выполните моделирование при шагах 0,001 и 0,0001; сделайте выводы по поводу выбора шага в данной задаче.
Ответ:
Уменьшение шага дискретизации меньше 0,001 с не приводит к изменению результата. Значит, можно использовать шаг 0,001 с.
Уровень C.
-
*Выполните моделирование движения мяча, брошенного под углом 45° к горизонту (при тех же остальных условиях, что и в задаче уровня B):
-
определите время полета, максимальную высоту и дальность полета мяча, скорость в момент приземления; -
сравните результаты со случаем, когда сопротивление воздуха не учитывается
без учёта
сопротивления
с учётом
сопротивления
ошибка (%)
Время полета, с
2,88
2,81
2,5%
Максимальная высота, м
10,19
9,65
5,6%
Дальность полета, м
40,77
44,93
9,3%
Скорость приземления, м/с
20
22,61
11,5%
-
сделайте выводы
Ответ:
В этой задаче нельзя не учитывать сопротивление воздуха. Это упрощение приводит к существенным ошибкам (более 10% по скорости).
-
Постройте с помощью табличного процессора две траектории движения шарика: без учёта и с учётом сопротивления воздуха:
Ответ:
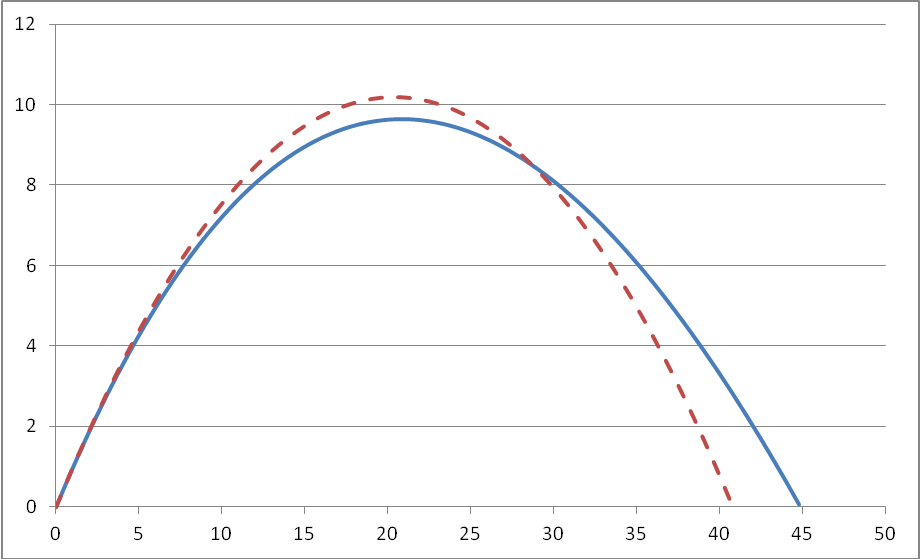
-
Выберите интервал дискретизации и обоснуйте его выбор:
Ответ:
Достаточно выбрать интервал дискретизации 0,001 с. Дальнейшее уменьшение не приводит к изменению результата.
- 1 2 3 4 5 6
Моделирование развития популяции
Для выполнения работы откройте файл-заготовку Популяция.xls.
Уровень A.
-
Постройте графики изменения численности популяции животных для моделей ограниченного и неограниченного роста при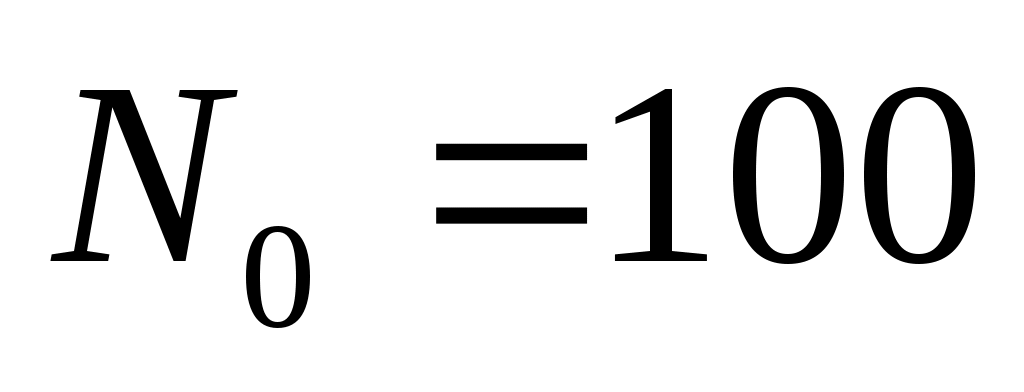 ,
, 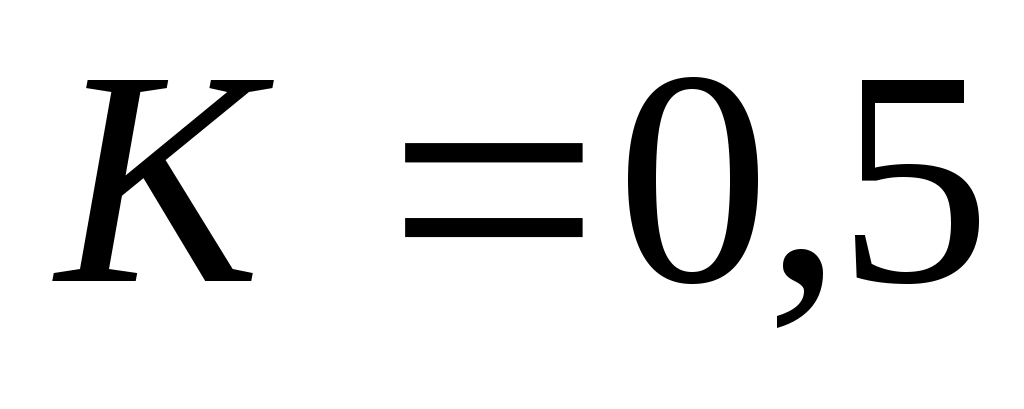 и
и 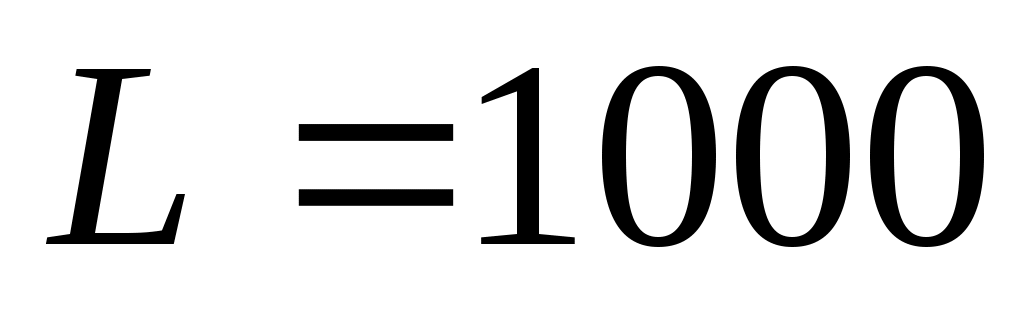 в течение первых 15 периодов. Определите, когда модель неограниченного роста перестает быть адекватной (отклонение от модели ограниченного роста составляет более 10%).
в течение первых 15 периодов. Определите, когда модель неограниченного роста перестает быть адекватной (отклонение от модели ограниченного роста составляет более 10%).
Ответ:
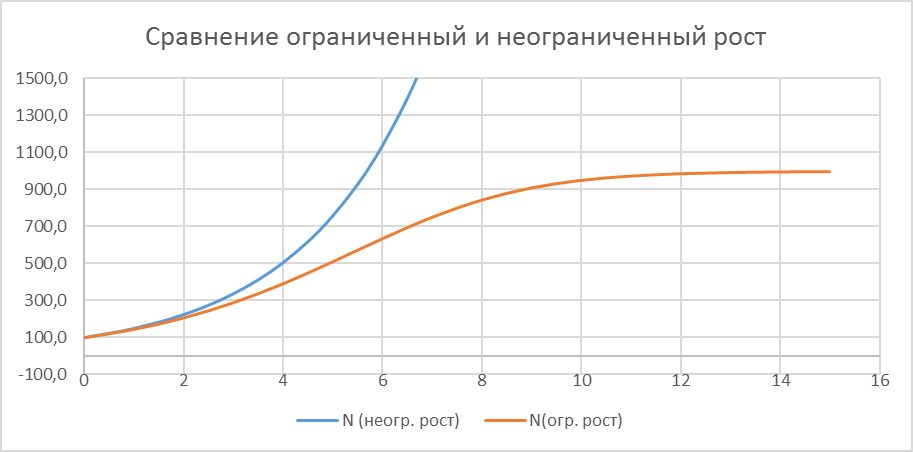
через 3 года
-
Используя подбор параметра, определите, при каких коэффициентах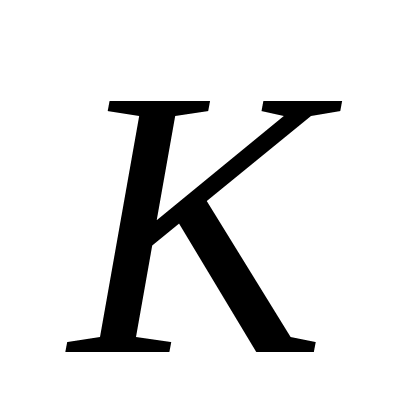 модель неограниченного роста остается адекватной в течение не менее 10 периодов.
модель неограниченного роста остается адекватной в течение не менее 10 периодов.
Ответ:
< 0,075
-
Используя модель ограниченного роста из предыдущей задачи, выполните моделирование популяции с учетом отлова (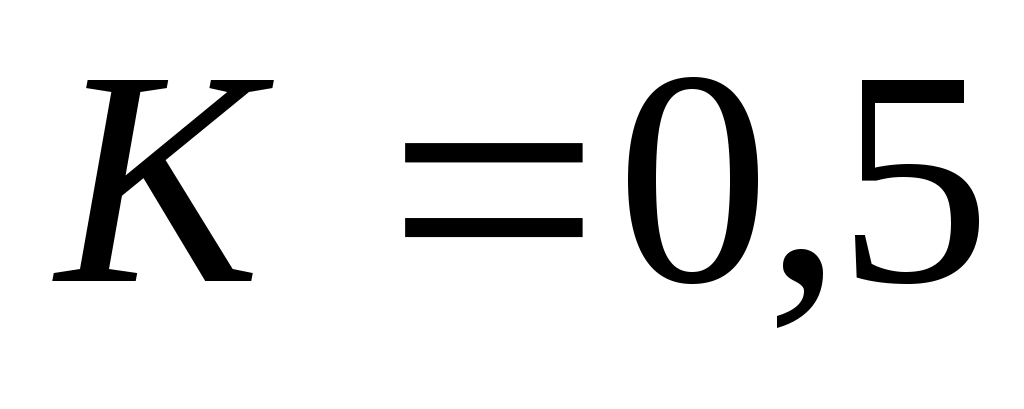 ,
, 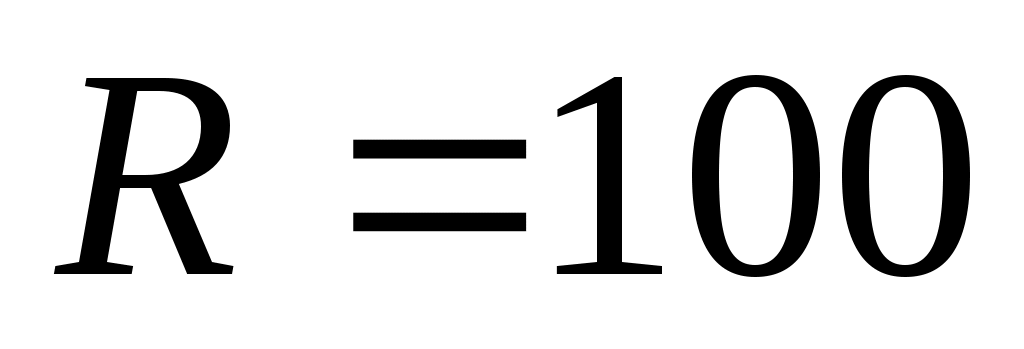 ). Предполагается, что животных начали отлавливать через 10 лет после начала наблюдений.
). Предполагается, что животных начали отлавливать через 10 лет после начала наблюдений.
-
постройте график изменения численности животных в течение 40 периодов;
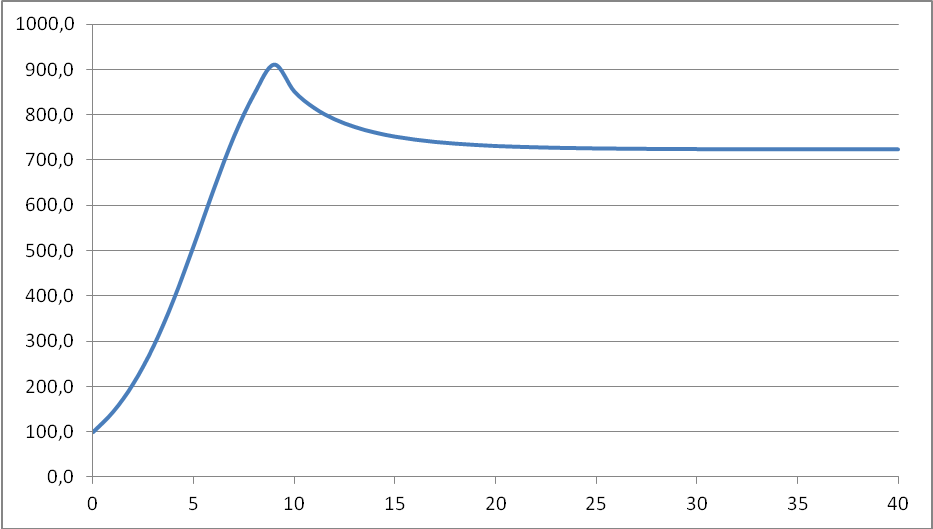
-
определите количество животных в состоянии равновесия по результатам моделирования;
Ответ:
724
-
проверьте, зависит ли оно от начальной численности?
Ответ:
не зависит
Уровень B.
-
Определите количество животных в состоянии равновесия теоретически, из модели ограниченного роста с отловом; сравните это значение с результатами моделирования
Ответ:
723,6
-
Определите, на что влияет начальная численность животных;
Ответ:
на начальный участок графика (до установления равновесия)
-
Определите (по результатам моделирования) максимальный отлов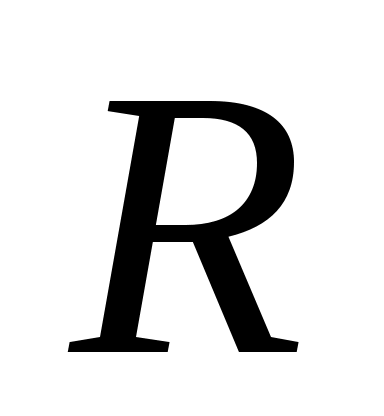 , при котором популяция не вымирает.
, при котором популяция не вымирает.
Ответ:
125
Уровень C.
-
*Определите максимально допустимый отлов теоретически, из модели ограниченного роста с отловом; сравните это значение с результатами моделирования
Ответ:
125
Из какого условия вы нашли это значение?
дискриминант уравнения (K/L)N2-KN+R=0 равен нулю
-
Моделирование эпидемии
Для выполнения работы откройте файл-заготовку Эпидемия.xls.
При эпидемии гриппа число больных
где
где
Считается, что в начале эпидемии заболел 1 человек, все заболевшие выздоравливают через 7 дней и больше не болеют.
Выполните моделирование развития эпидемии при