Файл: Моделирование работы процессора.doc

3. 
   Какова численность белок и бурундуков в состоянии равновесия?
   

Ответ:

64 белки

38 бурундуков

4. 
   Что влияет на состояние равновесия, коэффициенты модели или начальная численность?
   

Ответ:

коэффициенты

5. 
   На что влияет начальная численность животных?
   

Ответ:

на начальный участок графиков до установления равновесия

Уровень B.

6. 
   При каком значении коэффициента через 30 лет останется 30 бурундуков? (используйте подбор параметра).
   

Ответ:

DM = 0,13

7. 
   Сколько тогда будет белок?
   

M = 65

8. 
   Найдите какие-нибудь значения коэффициента , при котором модель становится неадекватна;
   

Ответ:

DM = 0,2

появление отрицательных значений

Уровень C.

9. 
   *Предложите аналогичную модель взаимного влияния трех видов.
   

Ответ:

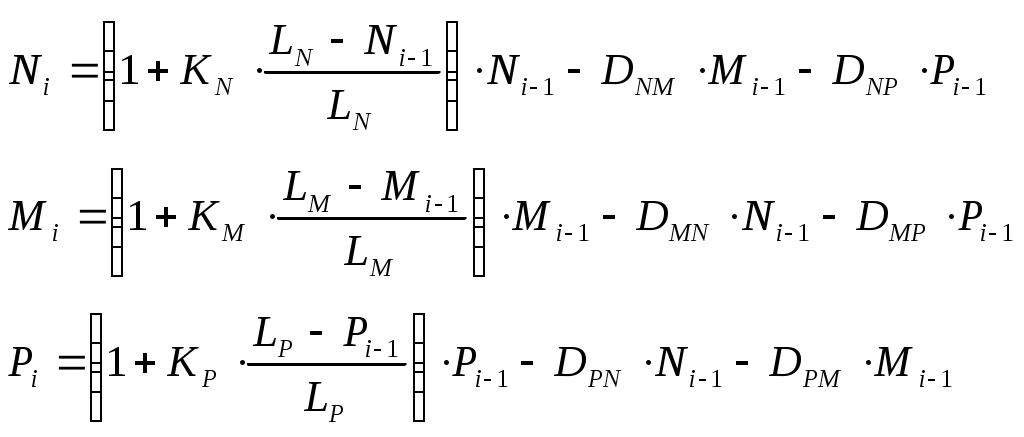
6. 1   2   3   4   5   6

---

Саморегуляция

Для выполнения работы откройте файл-заготовку Саморегуляция.xls.

Биологи выяснили, что для каждого вида животных существует некоторая минимальная численность популяции, которая необходима для выживания этой колонии. Это может быть одна пара животных (например, для ондатр) или даже тысячи особей (для американских почтовых голубей). Если количество животных становится меньше этого минимального значения, популяция вымирает. Для этого случая предложена следующая модель изменения численности:

, (*)

Эта модель отличатся от модели ограниченного роста только дополнительным множителем , где и – некоторые числа (параметры), смысл которых вам предстоит выяснить.

Уровень A.

1. 
   Выполните моделирование для 30 периодов при следующих значениях параметров модели:
   

Постройте на одном графике кривые, показывающие изменение численности по классической модели ограниченного роста и по модели (*).



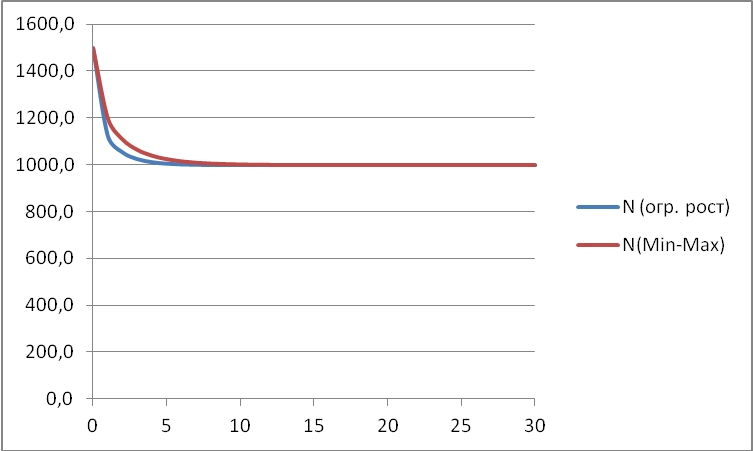
Сделайте выводы и опишите, в чём проявляется саморегуляция для этих моделей.

Ответ:

Если N₀ > L, восстанавливается предельная численность L

2. 
   Постройте аналогичные графики для F = 500:
   

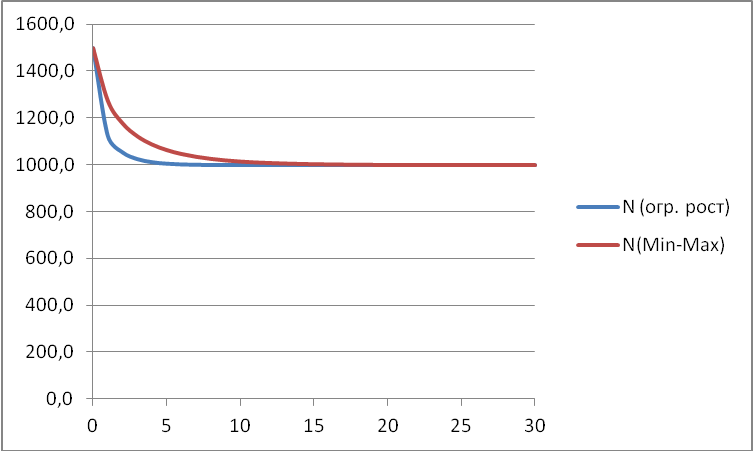
Сделайте вывод о том, как коэффициент F на саморегуляцию.

При увеличении F переход к установившемуся значению выполняется более плавно.

3. 
   Через 10 периодов в результате изменения природных условия число животных уменьшилось до 400 (то есть,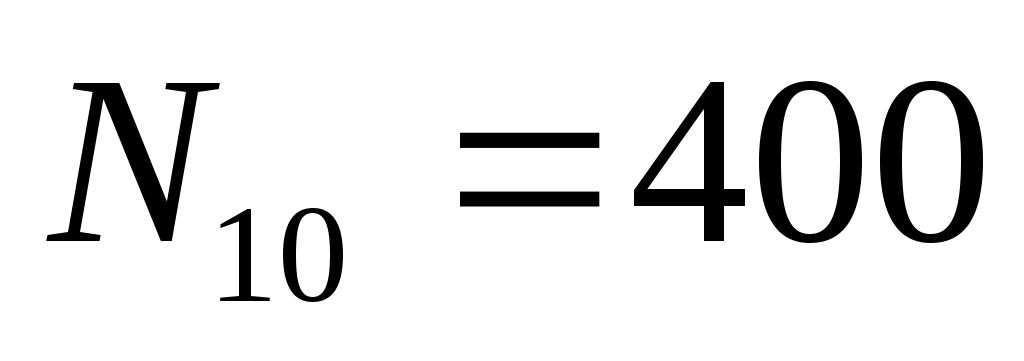 ). Используйте значение F = 500. Выполните моделирование при этих условиях и постройте графики:
   

---

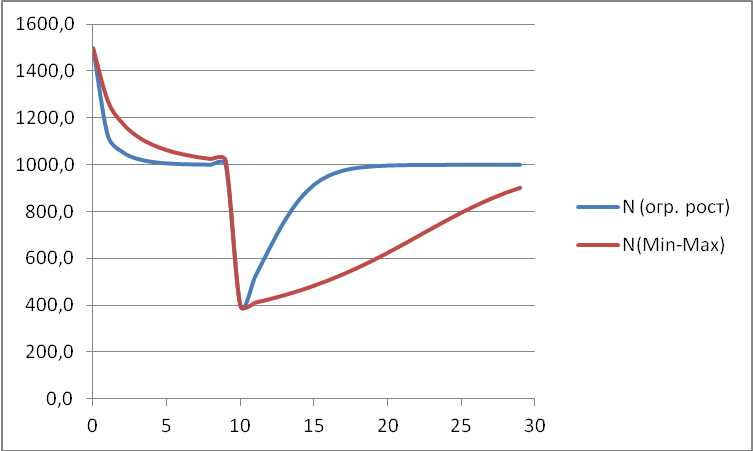
Опишите, чем отличается поведение двух сравниваемых моделей.

Численность L по модели (*) восстанавливается более плавно.

Как влияет изменение F на переходные процессы?

При увеличении F переход к установившемуся значению выполняется более плавно.

Уровень B.

4. 
   Повторите моделирование п. 3 при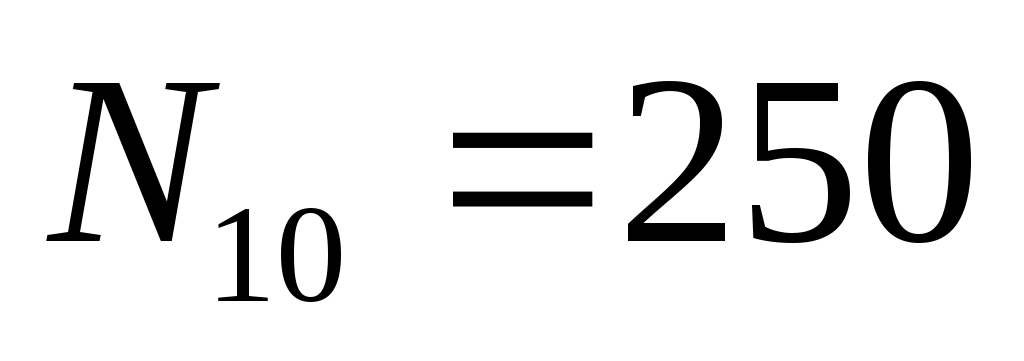 и постройте графики:
   

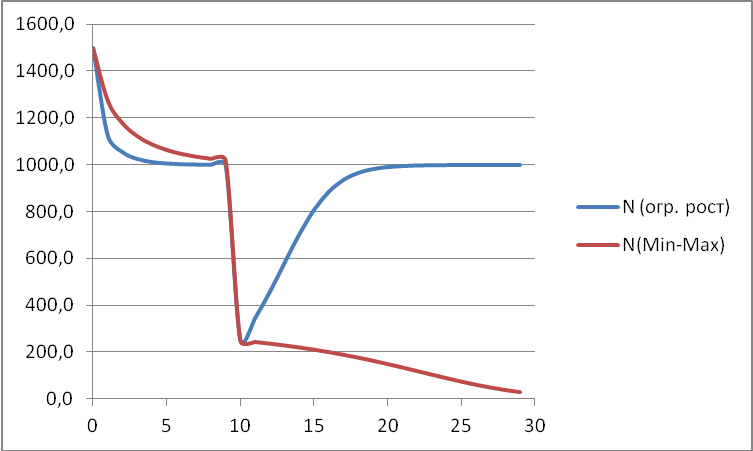
Cделайте выводы:

В этом случае саморегуляция в модели (*) не сработала, популяция вымерла. Возможно, из-за слишком маленькой численности N₁₀.

Уровень C.

5. 
   Экспериментируя с моделями, найдите минимальную численность популяции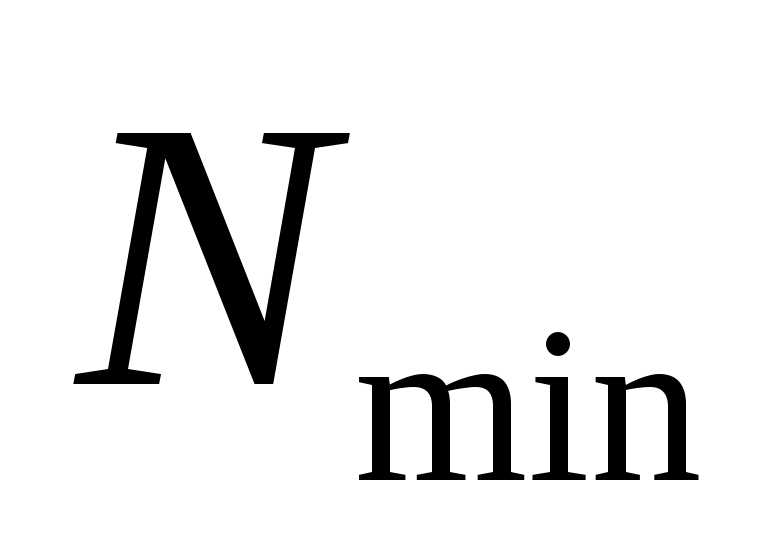 , при которой она выживает в соответствии с моделью (*).
   

Ответ:

300

6. 
   Сделайте выводы о смысле коэффициента в модели (*).
   

Ответ:

M – это минимально допустимая численность. Если число животных меньше, чем M, саморегуляция не работает.

7. 
   Сравните свойства саморегуляции для модели ограниченного роста и модели (*).
   

Ответ:

В модели ограниченного роста саморегуляция работает всегда, а в модели (*) – только при численности, большей, чем M.

6. 
   Методы Монте-Карло

Уровень А.

1. 
   Используя метод Монте-Карло, приближённо определите значение числа  (см. § 12 учебника). Запишите в таблицу полученные результаты при различных значениях N:
   

N	100	1000	10000	100000	1000000
Результат ( )	2,68	3,068	3,1264	3,1418	3,14272
Ошибка , %	14,693%	2,343%	0,484%	0,007%	0,036%

---

Относительная ошибка в процентах вычисляется по формуле

,

где  = 3,1415926… и – приближённое значение числа , полученное в результате моделирования.

Уровень B.

2. 
   Не используя значение , с помощью метода Монте-Карло вычислите площади кругов различного диаметра (с тремя знаками в дробной части):
   

   R	1	2	3	4	5
   S	3,141	12,565	28,279	50,244	78,454

3. 
   С помощью электронных таблиц постройте по этим данным зависимость S от R.
   
4. 
   Используя линию тренда, подберите функцию, которая лучше всего соответствует этой зависимости.
   

Ответ:

5. 
   Сравните эту функцию с известной вам формулой площади круга. Сделайте выводы.
   

Выводы:

Формулы построена в целом правильно, но с некоторой погрешностью в коэффициенте и показателе степени.

Уровень C.

6. 
   Не используя значение , с помощью метода Монте-Карло вычислите объёмы шаров различного диаметра:
   

   R	1	2	3	4	5
   V	4,189	33,512	113,094	268,008	523,751

7. 
   С помощью электронных таблиц постройте по этим данным зависимость V от R.
   
8. 
   Используя линию тренда, подберите функцию, которая лучше всего соответствует этой зависимости.
   

Ответ:

9. 
   Сравните эту функцию с известной вам формулой объёма шара. Сделайте выводы.
   

Выводы:

Формулы построена в целом правильно, но с некоторой погрешностью в коэффициенте и показателе степени.

---

6. 
   Системы массового обслуживания

Для моделирования обслуживания клиентов в банке предложена следующая модель:

• 
  за 1 минуту в банк входит случайное число клиентов, от 0 до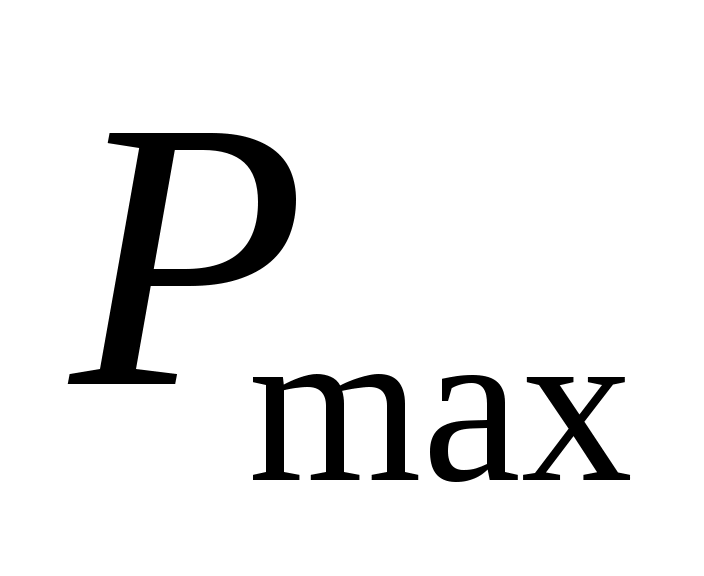 (распределение равномерное);
  
• 
  на обслуживание клиентов требуется от до 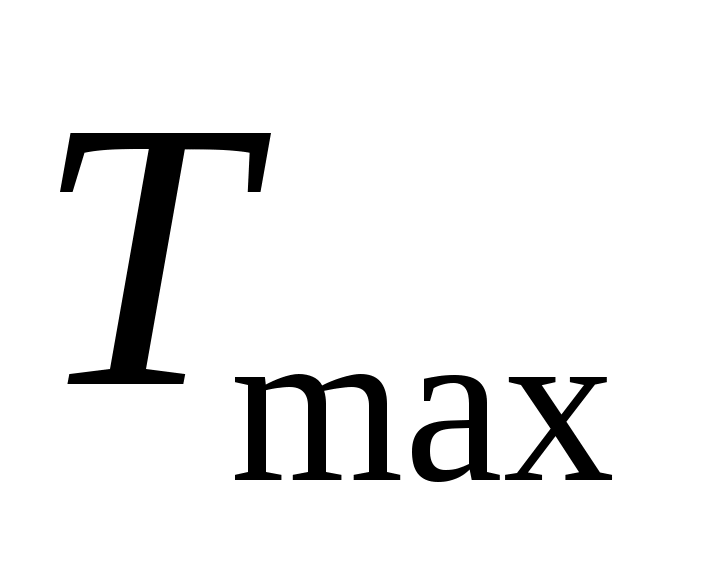минут; время обслуживания 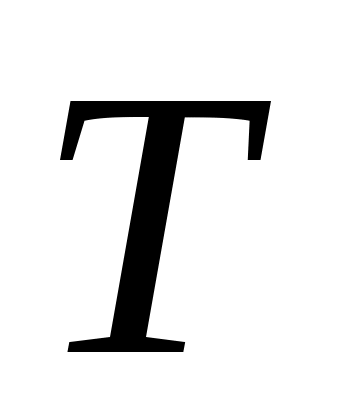определяется для каждой рабочей минуты случайным образом (распределение равномерное);
  
• 
  моделирование выполняется для интервала времени , равного 8-часам (рабочая смена).
  
• 
  число клиентов, находящихся в помещении банка, вычисляется по формуле
  

где – количество клиентов, вошедших за -ую минуту, а – количество клиентов, обслуженных за это время;

• 
  если кассир обслуживает клиента за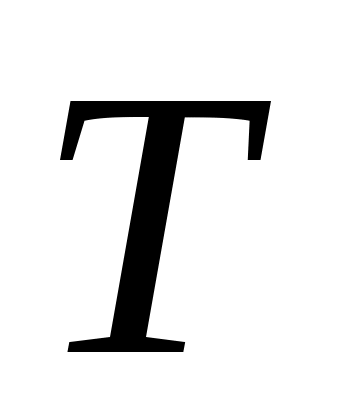 минут, то можно считать, что за 1 минуту он сделает часть работы, равную 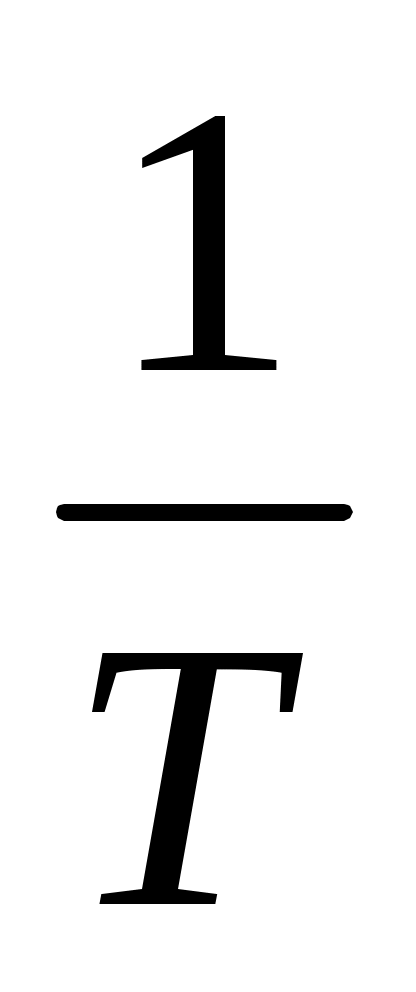; если предположить, что скорость работы кассиров одинакова, то касс за 1 минуту обслужат 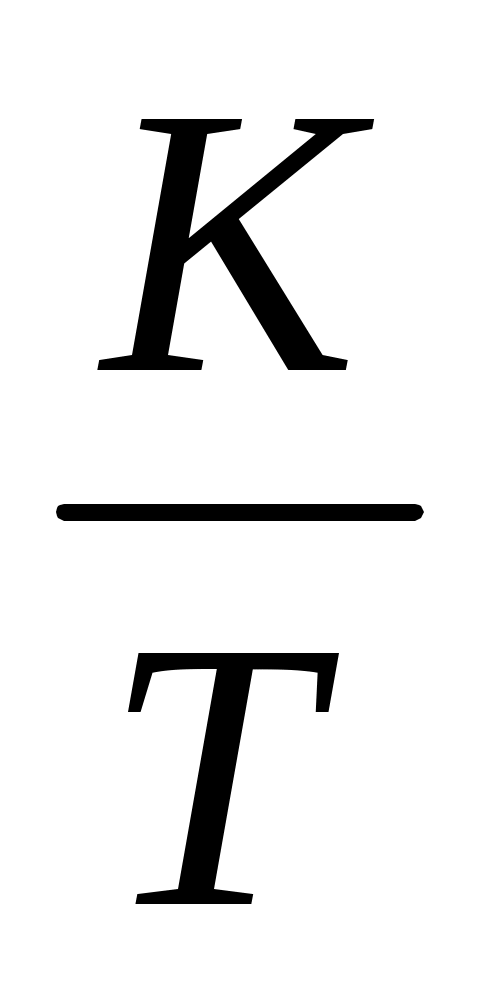клиентов;
  
• 
  если считать, что клиентов равномерно распределяются по кассам, так что средняя длина очереди равна 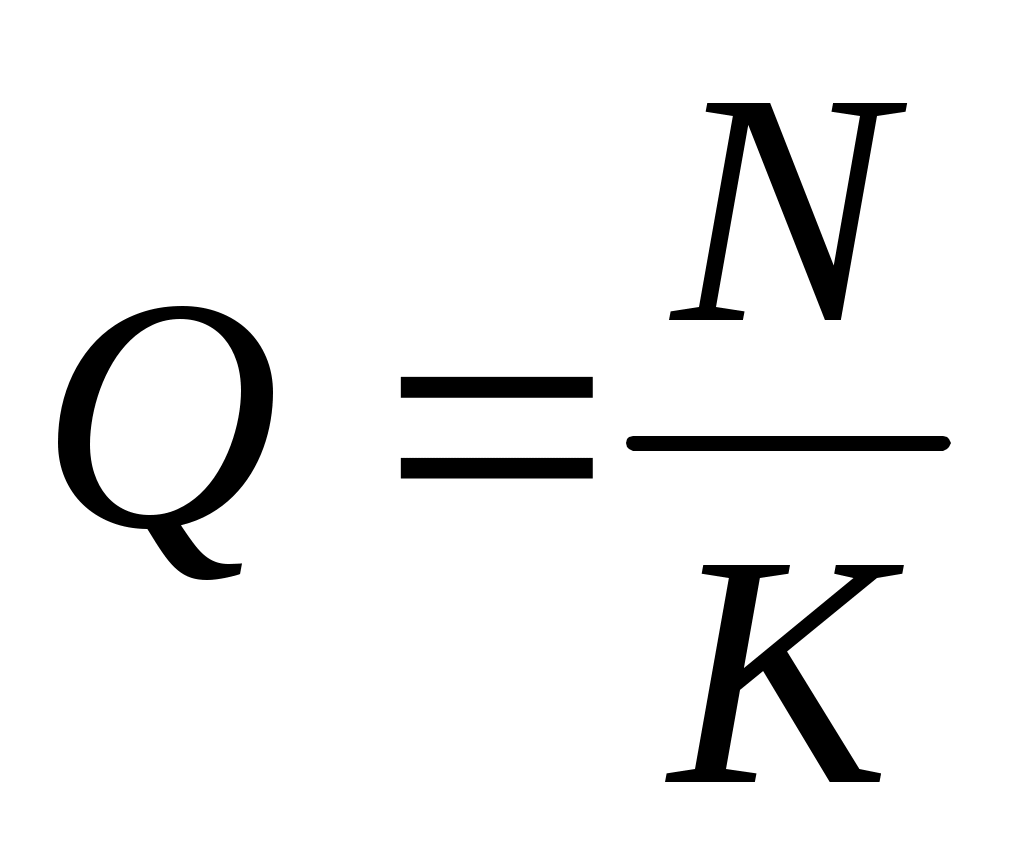, а среднее время ожидания в течение этой минуты равно
  

---