Файл: ВсяМехЛАБраб2части.doc

(7), где А’_тр.2 — работа по преодолению силы трения за N₂ оборотов колеса. С другой стороны по основному закону динамики вращательного движения: (8), гдеи, гдеr_в - радиус конической поверхности, по которой действует сила трения (внутренний радиус шкива или радиус вала). Отсюда, зная I можно оценить силу трения.

Покажем, как можно экспериментально определить момент инерции махового колеса. Из (7) выразим А и подставим в (6):

(8), или

(9).

Так как и, гдеt – время падения груза с высоты h, r – наружный радиус шкива (радиус поверхности, с которой сматывается нить!!!), уравнение (9) примет вид: .

Откуда 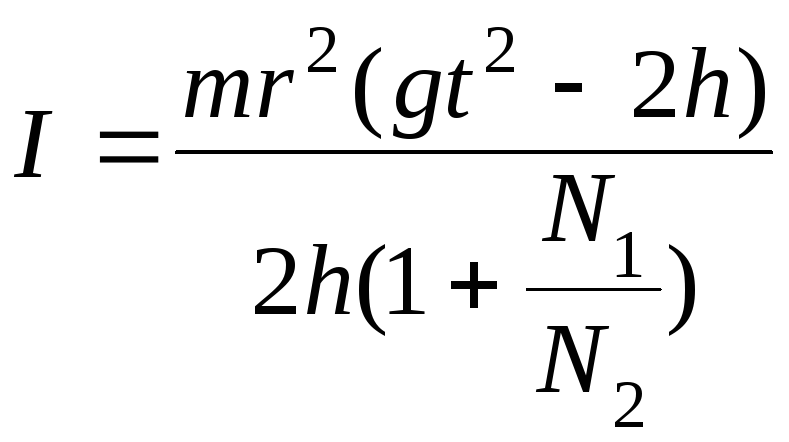 (10)

Если N – число оборотов от начала движения до полной остановки колеса, то N₂=N-N₁,  r - ?.

Вопросы к допуску:

1. Что такое момент инерции? В каких единицах он измеряется?

2. Когда говорят о вращательном движении? Дать определение.

3. Какова связь линейных и угловых величин?

4. Можно ли считать движение груза равноускоренным? Является ли оно таковым в реальности? Какие пренебрежения имеют место по ходу вывода расчетной формулы?

5. Записать расчетную формулу и пояснить все входящие в нее величины. Как по ходу работы вы будете получать их значение?

6. Что еще надо измерить, чтобы стало возможной оценка величины силы трения? О какой силе трения здесь идет речь? Между какими поверхностями она действует?

7. Расскажите об устройстве прибора.

8. Радиусы каких сечений используются при расчете в работе?

Содержание экспериментальных заданий

Задание 1.Определение момента инерции махового колеса.

1. Измерить штангенциркулем диаметр шкива и определить его радиус r.

2. Измерить расстояние h от нижней части висящего груза до пола. Рекомендуется не менять по ходу выполнения всего задания.

3. Измерить время t падения груза секундомером.

4. Подсчитать число оборотов N колеса от начала вращения до остановки и число оборотов N₁ до падения груза.

5. Момент инерции вычислить по формуле (10) в системе СИ.

6. Проделать опыт несколько раз, занося результаты отдельных отсчетов в таблицу 1.

   №	m, кг	r, м	h, м	t, с	N1	N	N2	I, кг∙м2
   1.
   2.
   3.

7. Оценить погрешность результата, как косвенного измерения.

8. Записать полученный результат с указанием границ погрешности.

Задание 2.Оценка величины силы трения между валом и шкивом.

1. Измерить диаметр вала и вычислить его радиус .

2. Вывести формулу для силы трения в используемом приборе на основе положений, приведенных выше.

3. Произвести расчеты 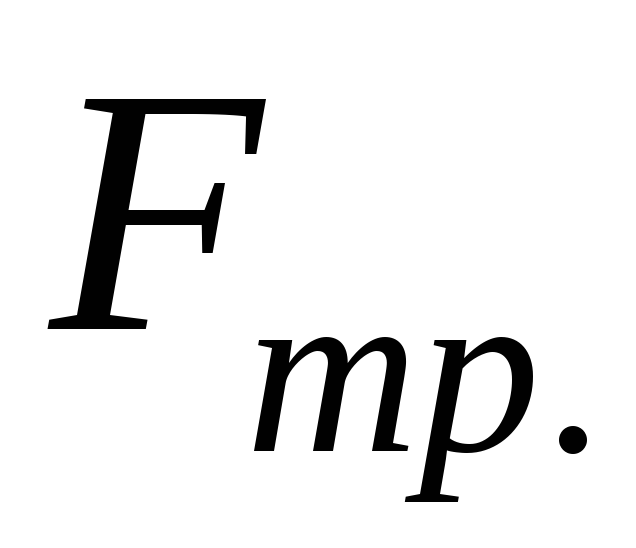и ее момента.

4. Сравнить по величине вращающие моменты сил, действующих на маховое колесо при ее вращении по заданию 1.

5. Сделать вывод.

Вопросы к отчету.

1. Что называется моментом инерции точки и тела относительно оси вращения? От чего зависит момент инерции тела? Какую роль он играет во вращательном движении?

2. Запишите основной закон динамики вращательного движения.

3. Как он запишется применительно к маховому колесу до и после падения груза? Какие силы обеспечивают вращение махового колеса в каждом из этих случаев?

4. Приведите план вывода формулы для расчета момента инерции однородного диска.

5. Каким будет движение махового колеса при отсутствии трения?

6. Назвать вид движения маховика и груза, подвешенного к нити. Записать кинематические и динамические уравнения движения груза и маховика.

7. Сформулируйте закон сохранения и изменения механической энергии.

8. Вывести расчетную формулу.

9. Вывести формулу для момента инерции маховика без учета силы трения.

Лабораторная работа № 2.4.

Определение момента инерции тел различной формы

методом крутильных колебаний.

Цель работы: экспериментальное определение момента инерции образцов методом трифилярного подвеса и проверка теоремы Штейнера.

Приборы и принадлежности: трифиляр, секундомер, штангенциркуль, масштабная линейка, весы, образцы для измерения.

Описание прибора и теория метода.

Одним из методов определения момента инерции тел является метод трифилярного подвеса. Трифиляр представляет собой круглую платформу, подвешенную на 3-х симметрично расположенных нитях (рис.1). Верхние концы нитей симметрично прикреплены к диску. Платформа может совершать крутильные колебания вокруг вертикальной оси, перпендикулярной к ее плоскости и проходящей через ее центр.

Вращательный импульс, необходимый для начала крутильных колебаний, сообщается платформе путем поворота верхнего диска вокруг его оси.

При крутильных колебаниях платформы ее центр масс перемещается по оси вращения, занимая наивысшее положение при максимальном отклонении платформы от положения равновесия и наинизшее при прохождении положения равновесия.

Если платформа массы m, вращаясь в одном направлении, поднялась на высоту h, то приращение потенциальной энергии будет равно , гдеg – ускорение свободного падения.

Вращаясь в другом направлении платформа придет в положение равновесия с кинетической энергией, равной ,I – момент инерции платформы, - угловая скорость платформы в момент достижения ею положения равновесия.

Пренебрегая работой сил трения, на основе закона сохранения механической энергии имеем: или(1).

Если l – длина нитей подвеса, R – радиус платформы, r – радиус верхнего диска, то по рис.2 определим h.

В положении равновесия центр нижнего диска находится в точке О. Рассмотрим радиус диска ОА. При его повороте на угол  центр нижнего диска переходит в точку О₁ и приподнимается на расстояние , гдеd и d₁ - расстояние между верхним и нижним дисками соответственно в положении равновесия и при повороте на угол  нижнего диска относительно верхнего.

Далее требуется провести ряд математических преобразований, чтобы выразить приблизительно высоту подъема h через радиусы дисков и длину нитей, т.е. через R, r и l. Запишем: 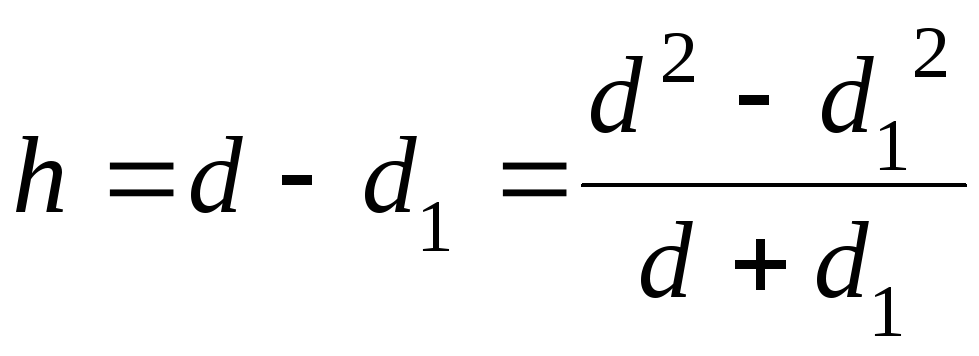(2). Из прямоугольного треугольника ВВ₂А: , аналогично из ВВ₁А₁ найдем d₁, где В₁А₁ выражаем по теореме косинусов из треугольника В₁О₁А₁: . Подставим в (2):

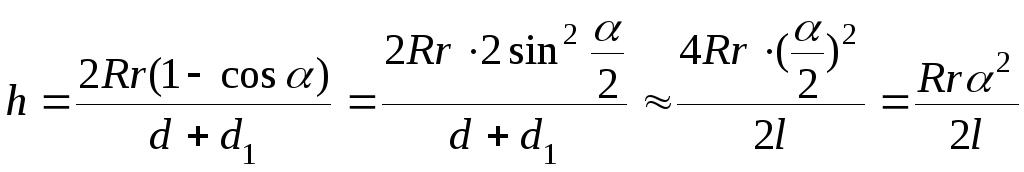(3), где приближенные замены оправданы в случае большой длины нитей l и малых углах отклонений  при крутильных колебаниях нижнего диска трифиляра (это дает приближение данного движения в форме гармонических колебаний).

Подставляя (3) в (1), получаем: . Продифференцировав это выражение по времени, сократив наи поделив наI, получим уравнение движения системы: 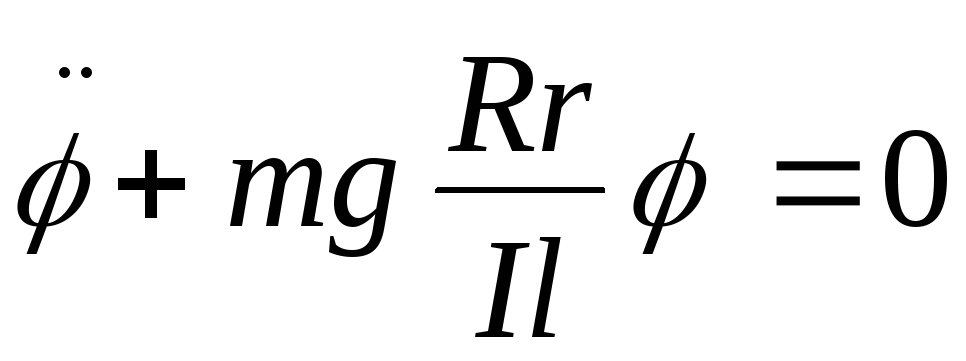(4). Решение этого уравнения имеет вид: