Файл: ВсяМехЛАБраб2части.doc

Описание установки и метода

Б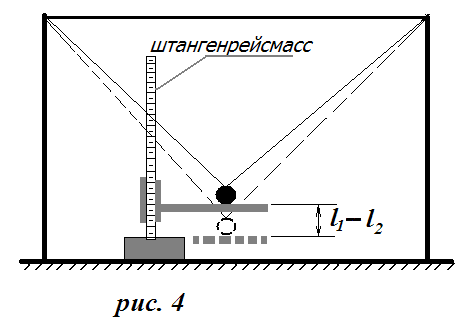ольшинство косвенных методов измерения ускорения свободного паденияg основано на использовании формулы (9) для периода гармонических колебаний математического маятника.

Пусть нам известны периоды двух математических маятников различной длины. Тогда можно записать на основе (9):

и .

Возводим оба равенства в квадрат и находим их разность:

.

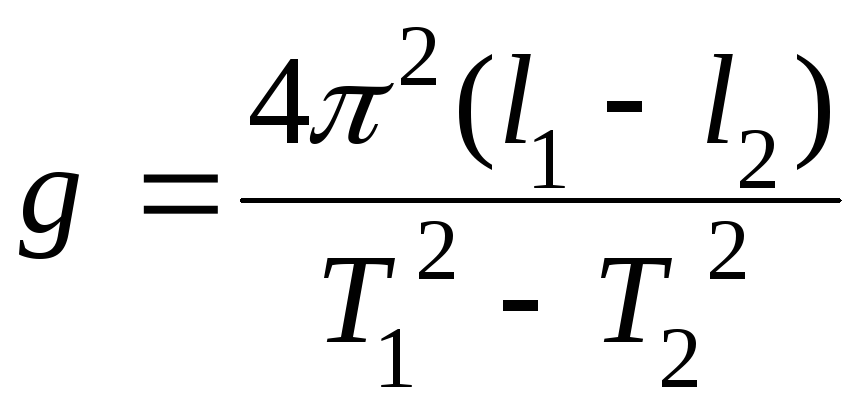Если определять период по времени t совершения маятником N колебаний, т.е. . Тогда расчетная формула примет окончательный вид:

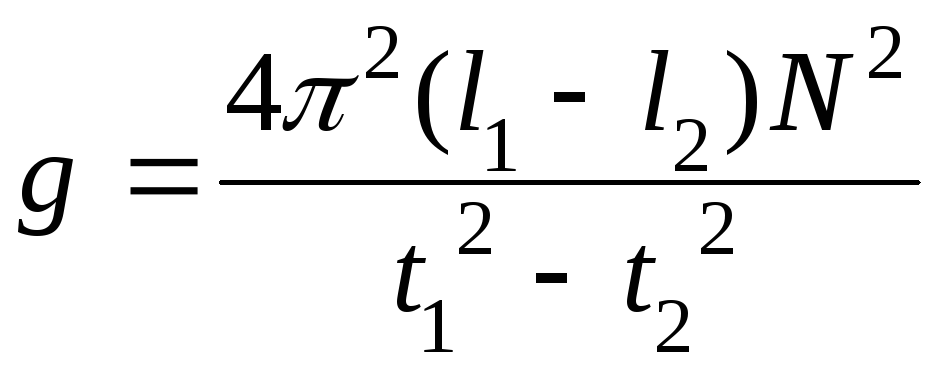(10) - расчетная формула для ускорения свободного падения.

В работе рекомендуется использовать бифилярный маятник – груз, подвешенный на двух расходящихся нитях (рис.4). При этом сама длина соответствующего математического маятника НЕ измеряется, а измеряется разность длин (l₁-l₂) с помощью штангенрейсмасса.

Вопросы к допуску:

1. Какое движение называется колебаниями?

2. Что такое математический маятник?

3. Дайте определение и запишите формулы для вычисления периода математического маятника.

4. Как с помощью математического маятника можно найти величину ускорения свободного падения?

5. Записать расчетную формулу для нахождения ускорения свободного падения и пояснить, как в работе находятся значения входящих в нее величин.

6. Что представляет собой штангенрейсмасс? Его назначение.

7. Можно ли с его помощью измерить длину математического маятника? Для измерения какой величины он используется в данной работе?

8. Почему углы отклонения должны быть малыми?

Содержание экспериментальных заданий

Задание1.Определение ускорения свободного падения с помощью математического маятника.

1. Установить бифилярный маятник так, чтобы длины двух нитей были равны – симметричное расположение шарика на нитях.

2. Отметить по шкале штангенрейсмасса положение нижней точки шарика, занести результат отсчета по шкале в тетрадь.

3. Отклонить на небольшой угол шарик и отпустить.

4. Включить секундомер (при прохождении шарика положения равновесия или в положении его максимального отклонения от положения равновесия) и измерить время, за которое будет совершено 20, 30 и 50 колебаний.

5. Поднять шарик, одинаково укоротив обе нити.

6. Отметить по шкале штангенрейсмасса второе положение шарика, отсчет по шкале записать.

7. Вычислить разность отсчетов по шкале штангенрейсмасса, т.е. расстояния между двумя использованными положениями шарика.

8. С помощью секундомера аналогично п.4) произвести измерение промежутков времени, за которые будет совершено 20, 30 и 50 колебаний.

9. Результаты измерений занести в таблицу 1. Таблица 1.

   	первый маятник		второй маятник		l1-l2, м	g, м/с2
   N	отсчет по шкале, м	t1, с	отсчет по шкале. м	t2, с
   20
   30
   50

10. Вычислить по (10) ускорения свободного падения по данным для 20, 30 и 50 колебаний.

11. Сделать вывод о влиянии выбора числа совершаемых за отмеряемое время колебаний на точность результата вычисления величины g.

12. Пользуясь известным значением g из таблицы (см. в конце книги) для широты вашей местности, произвести вычисление абсолютной и относительной погрешностей для среднего значения результатов косвенного измерения величины ускорения свободного падения.

13. Записать результат в виде ,.

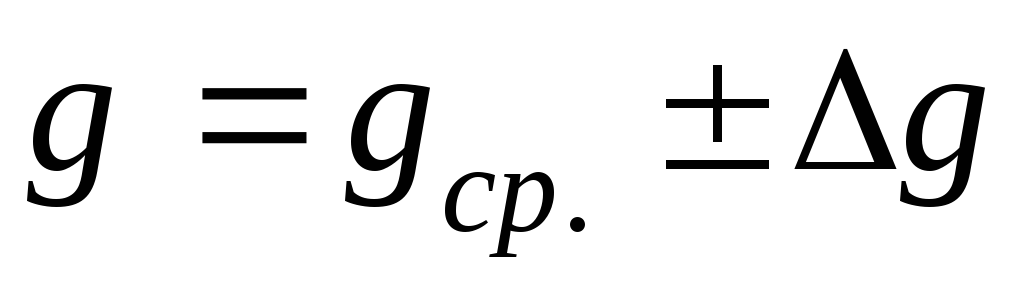Вопросы к отчету.

1. Какие колебания называются гармоническими? Дать определение их основных характеристик (амплитуды, фазы, периода, частоты, циклической частоты).

2. При каких условиях колебания математического маятника можно считать гармоническими?

3. Какая сила называется квазиупругой?

4. Какая сила выполняет роль возвращающей силы в случае математического маятника? Доказать, что она является квазиупругой.

5. Вывести формулу периода колебаний математического маятника, определив двумя способами коэффициент квазиупругости k системы.

6. Вывести расчетную формулу.

Приложение 1.

Оценка погрешностей лабораторных измерений и

вычислений по физике.

Измерение как метод познания – специфическое сравнение данной величины с некоторым его значением, принятым за эталон, с целью получения ее количественного значения. Специфическое – основанное на создании и использовании специальной измерительной техники, определенных физических процессов и материальных орудий в качестве средств измерения, а также некоторых теоретических предпосылок.

Способ измерения включает в себя 3 главных момента: 1) выбор единицы измерения и получение набора соответствующих мер; 2) установление правила сравнения измеряемой величины с мерой и правило сложения мер; 3) описание процедуры сравнения.

Измерения делятся на:

1. прямые – при которых измеряемая величина непосредственно сравнивается с эталоном или определяется с помощью измерительного прибора, проградуированного в соответствующих единицах;

2. косвенные – при которых производятся прямые измерения нескольких других величин, с которыми искомая величина функционально связана на основании определенной физической закономерности.

Из математики известен смысл функциональной зависимости: каждому набору значений аргументов (независимых аргументов – результатов прямых измерений) соответствует не более одного значения функции (зависимой переменной – результата косвенного измерения). Всякая функциональная зависимость, положенная в основу косвенного измерения, выражается формулой. Эта формула выражает определение (например, ,),закон (например, ,) или выведенноеследствие совокупности определений, законов, принципов и пр.

Абсолютно точных измерений не существует. Точная оценка границ погрешности также невозможна, а можно лишь определить степень доверия к полученному результату. Это значит, что можно определить ожидаемую воспроизводимость результатов при повторных измерениях.

При измерении различных физических величин исходят из той точности измерений, которая практически нас удовлетворяет.

Точность измерения характеризуется: 1) границами допущенной погрешности, т.е. самой погрешностью; 2) вероятностью того, что найденное приближенное значение заключено в этих пределах.

Общая погрешность складывается из погрешности отсчета (вследствие округления показаний до заданной степени точности, чаще она не превышает половины наименьшего деления шкалы прибора, но иногда необходимо учитывать субъективные причины возможных неточностей отсчета, обусловленные индивидуальными свойствами наблюдателя), инструментальной погрешности (обусловлена конструкцией прибора, обычно не превышает цены деления прибора) и случайной погрешности (обусловленной, например, неправильной установкой прибора, влиянием внешних условий).

Оценить погрешность – значит вычислить абсолютную погрешность, измеряемую в единицах той же физической величины. Абсолютная погрешность равна произведению относительной погрешности на значение самой величины.

Для характеристики погрешностей используют еще такие понятия:

• средняя квадратичная погрешность отдельных измерений – мера разброса результатов измерений ;

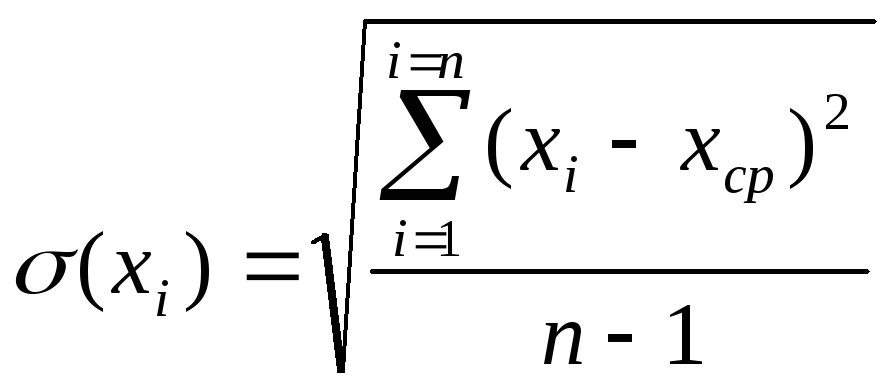• средняя квадратичная погрешность среднего значения ;

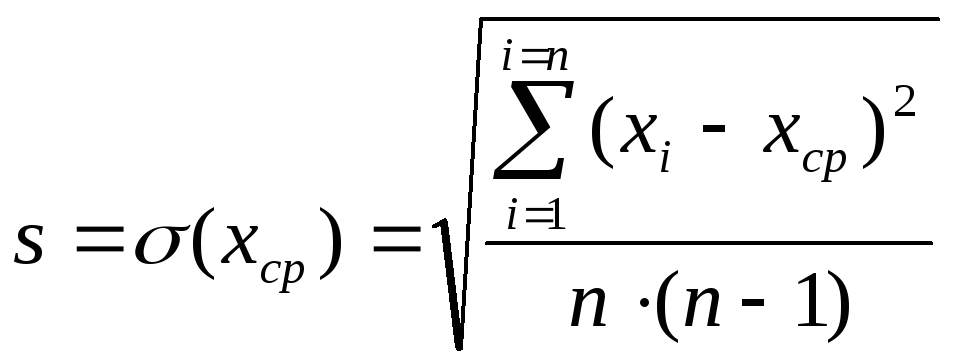• дисперсия – квадрат средней квадратичной погрешности s²;

• доверительный интервал Е, соответствующий доверительной вероятности Р_Е. Так, Е=ts, где t – любое число.

В случае малого числа измерений доверительный интервал среднего значения Е = х_ср – Х можно найти по формуле Стьюдента Е=t_ss, где t_s – коэффициент Стьюдента, который находится по таблице.

Табл. Значение t_s для различных значений доверительной вероятнотси Р_s и числа измерений n.