Файл: trigonometrich_ryad.doc

2. Тригонометрический ряд

Полезно рассмотреть частный вид функциональных рядов, так называемые тригонометрические ряды. Членами тригонометрических рядов служат тригонометрические функции sin nx и

cos nx (n=1,2,3,…), взятые с числовыми коэффициентами. Тригонометрические функции, так же как и степенные, используются для разложения по ним функций.

О п р е д е л е н и е 1. Функциональный ряд вида

+(cos nx+sin nx) (1)

где ,и вещественные числа, называется тригонометрическим рядом.

(Свободный член обозначается для удобства некоторых дальнейших выкладок).

Каждый член тригонометрического ряда является периодической функцией с периодом 2. Действительно, постояннуюможно, как известно, считать периодической функцией с каким угодно периодом, в частности с периодом2;sin x и cos x (п=1) имеют период 2;sin 2x и cos 2x (п=2), как известно, имеют период , следовательно, число2также является их периодом; вообщеsin пx и cos пx имеют период, равный , и, следовательно, числотакже является их периодом. Поэтому можно сказать, что если ряд (1) сходится, то его сумма является периодической функцией с периодом2.

---

Изучим одно свойство системы тригонометрических функций.

О п р е д е л е н и е 2. Система функций (х), (х),…, заданных в некотором промежутке , называется ортогональной системой в ,если

при nm (2)

и

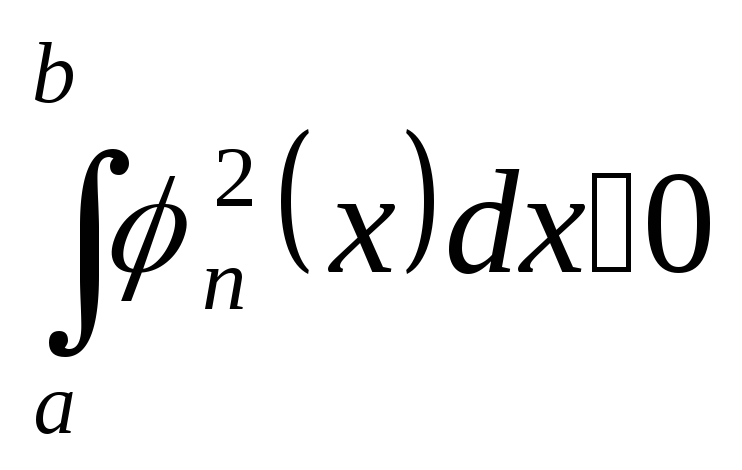при любом п.

(Последнее неравенство означает, в частности, что ни одна из функций системы не есть тождественный нуль.)

Т е о р е м а. Система функций

1, cos x, sin x, cos 2x, sin 2x,…, cos nx, sin nx,… (3)

является ортогональной системой в промежутке .

Доказательство. Проверим выполнение равенства (2) для функций системы (3). Для этого надо проверить непосредственным вычислением равенство нулю интегралов от произведений различных функций системы (3), то есть от произведения двух косинусов с разными аргументами, двух синусов с разными аргументами, произведения косинуса на синус (с любыми аргументами) и произведения любого синуса или любого косинуса из системы (3) на единицу, которая является первой функцией системы (3).

Итак, проводим указанные выкладки:

а)

б)

в) Пусть nm:

в силу пункта а), так как (m+n) и (m-n) – целые числа, отличные от нуля.

г) Пусть nm:

---

опять в силу пункта а).

д)

в силу пункта б) первый интеграл равен нулю; второй интеграл равен нулю в силу пункта б) при nm; если же n=m, то этот интеграл равен нулю потому, что подынтегральная функция тождественно равна нулю: sin(m-n)x=sin0=0.

Также проверяется легко и второе требование:

Таким образом, теорема доказана.

Примеры

№1Является ли система функций

ортогональной?

1.

2.

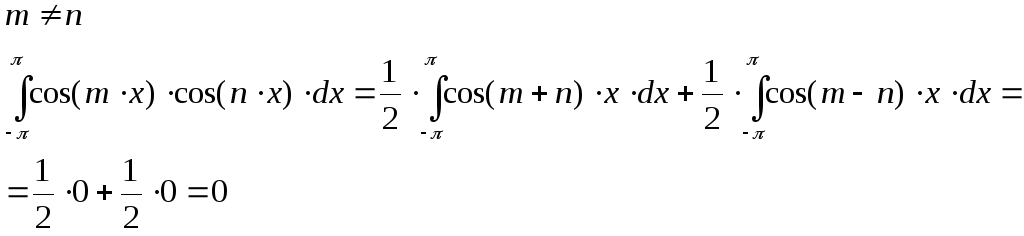
3.

Таким образом система является ортогональной.

№2Является ли система функций

ортогональной.

1.

2.

3.

Таким образом, система является ортогональной.

№3

---

Функция является ортогональной.

---

3. Ряд фурье

Ранее было введено понятие ряда Тейлора. Так был назван специальный ряд, коэффициенты которого вычислялись по определенному правилу с помощью некоторой заданной функции f(х). Таким образом, каждой бесконечно дифференцируемой функции ставился в соответствие ее ряд Тейлора.

Изучая тригонометрические ряды, можно пойти по такому же пути. Возьмем некоторую функцию f(х), определенную в (а может быть, и в большем промежутке или даже на всей числовой оси), и составим с ее помощью следующие числа:

, ,(1)

О п р е д е л е н и е. Тригонометрический ряд, коэффициентами которого служат числа (1), называется рядом Фурье функции f(х), а сами числа (1) называются коэффициентами Фурье функции f(х).

Для того чтобы можно было вычислить коэффициенты Фурье, нужно, очевидно, предположить, что функция f(х) интегрируема в .

Итак, каждой функции f(х), интегрируемой в , можно поставить в соответствие ее ряд Фурье:

f(х)~ (2)

Докажем предварительно следующее утверждение, относящееся к любому функциональному ряду.

Л е м м а. Если функциональный ряд сходится равномерно ви– некоторая ограниченная вфункция, то рядтакже равномерно сходится в.

Доказательство. Тот факт, что данный ряд равномерно сходится в означает следующее: для всякого ε>0 найдется номер N такой, что неравенство <ε справедливо для всякого n N и для любого

---