ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 17.04.2024
Просмотров: 95
Скачиваний: 0
Так как по условию
![]() ограничена в
ограничена в
![]() ,
то существует число М>0
такое, что
,
то существует число М>0
такое, что![]() <М
для всех
<М
для всех
![]() .
.
Возьмем любое ε>0.
Найдем по определению равномерной
сходимости ряда
![]() номер N
такой, что
номер N
такой, что
![]() <
<![]() для всех
для всех![]() .
Известно, что во всяком сходящемся ряде
множитель, общий для всех членов ряда,
можно «выносить за скобку». Поэтому
справедливо следующее равенство:
.
Известно, что во всяком сходящемся ряде
множитель, общий для всех членов ряда,
можно «выносить за скобку». Поэтому
справедливо следующее равенство:
![]()
Теперь, используя предыдущее неравенство, получаем:
![]()
Итак,
![]() <
<![]() дляn
дляn
![]() N
и для всех
N
и для всех
![]() .
Ввиду произвольности
.
Ввиду произвольности![]()
это и означает,
что ряд
![]() равномерно сходится в
равномерно сходится в
![]() .
.
Т е о р е м а. Если
функция f(х) разлагается на
![]() в равномерно сходящийся тригонометрический
ряд, то этот тригонометрический ряд
есть ее ряд Фурье.
в равномерно сходящийся тригонометрический
ряд, то этот тригонометрический ряд
есть ее ряд Фурье.
Доказательство.
Пусть для
![]()
![]()
![]() (3)
(3)
и ряд сходится
равномерно в
![]() .
Проинтегрируем обе части равенства (3)
в
.
Проинтегрируем обе части равенства (3)
в
![]() .
При вычислении интеграла от правой
части можно по условию теоремы
проинтегрировать ряд почленно:
.
При вычислении интеграла от правой
части можно по условию теоремы
проинтегрировать ряд почленно:
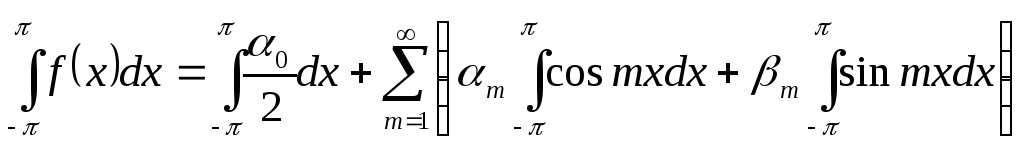
По теореме из § 1 (свойство ортогональности системы тригонометрических
функций) интегралы под знаком суммы равны нулю, и, таким образом, получаем:
![]() ,
,
откуда
![]() ,
то есть
,
то есть![]() (см. формулу (1)).
(см. формулу (1)).
Теперь умножим
обе части равенства (3) на cos
nx,
где п –
любое натуральное число, и проинтегрируем
опять в
![]() .
Умножение всех членов равномерно
сходящегося ряда на ограниченный
множитель cos
nx
в силу леммы не нарушает равномерной
сходимости ряда, и ряд в правой части
(3) можно опять интегрировать почленно:
.
Умножение всех членов равномерно
сходящегося ряда на ограниченный
множитель cos
nx
в силу леммы не нарушает равномерной
сходимости ряда, и ряд в правой части
(3) можно опять интегрировать почленно:
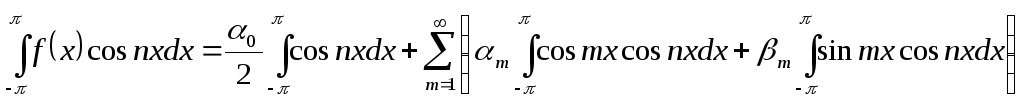 (4)
(4)
В силу теоремы из
§ 1 интеграл в первом слагаемом равен
нулю, первый из интегралов в скобках
равен нулю при n![]() m,
а второй – всегда равен нулю. Следовательно,
из всего ряда в правой части (4) остается
только слагаемое с номером n=m:
m,
а второй – всегда равен нулю. Следовательно,
из всего ряда в правой части (4) остается
только слагаемое с номером n=m:
![]()
(см. конец доказательства теоремы из § 1).
Таким образом,
равенство (4) принимает вид:![]() ,
откуда
,
откуда
![]() ,
то есть
,
то есть
![]() (см.(1)).
(см.(1)).
Таким же образом,
умножая обе части равенства (3) на sin
nx и интегрируя
почленно, получаем, что
![]() .
.
Итак, коэффициенты
тригонометрического ряда (3) совпадают
с коэффициентами Фурье функции f(х),
то есть ряд (3), действительно, является
рядом Фурье функции f(х)
4. Особенности ряда фурье четной и нечетной функций
Пусть функция f(х) задана на
 и четная.
и четная.
Проверим, что в этом случае коэффициенты Фурье bn функции f(х) равны нулю. Так как f(х) – четная функция, то произведение f(х)sin nx – нечетная функция (см. том I, гл. II, § 3), и в силу свойства интеграла от нечетной функции по промежутку, симметричному относительно нуля, можно сказать, что
![]() ,
то есть
,
то есть
![]() (1)
(1)
Формулам для
коэффициентов
![]() можно придать несколько иной вид.
Действительно, произведениеf(х)cos
nx
– четная функция и по свойству интеграла
от четной функции по промежутку,
симметричному относительно нуля, можно
написать (см. предыдущую ссылку):
можно придать несколько иной вид.
Действительно, произведениеf(х)cos
nx
– четная функция и по свойству интеграла
от четной функции по промежутку,
симметричному относительно нуля, можно
написать (см. предыдущую ссылку):
![]()
Итак,
![]() ,
,![]() (2)
(2)
Таким образом, ряд Фурье, соответствующий четной функции, содержит только члены с косинусом и свободный член:
![]() ~
~![]()
![]()
Пусть функция f(х) задана на
 и нечетная.
и нечетная.
Используя рассуждения, аналогичные приведенным выше, можно показать, что в этом случае
![]()
![]() (3)
(3)
![]() (4)
(4)
и поэтому нечетной функции соответствует ряд Фурье, содержащий только члены с синусами:
![]() ~
~![]()

5. Сходимость ряда фурье
Соотношение (2) из
§ 2 оставляет открытым вопрос о том,
сходится ли ряд Фурье функции f(х)
в
![]() ,
и, если сходится, то к какой функции он
сходится: к функции f(х),
породившей этот ряд, или к какой-либо
другой функции?
,
и, если сходится, то к какой функции он
сходится: к функции f(х),
породившей этот ряд, или к какой-либо
другой функции?
Аналогичный вопрос
ставился и в гл. XXII
при рассмотрении ряда Тейлора функции
f(х).
Там были даны условия, необходимые и
достаточные для того, чтобы ряд Тейлора
функции f(х)
сходился в
![]() именно к самой этой функции. Поскольку
не всякая бесконечно-дифференцируемая
функция, то есть такая функция, которой
можно поставить в соответствие ее ряд
Тейлора, удовлетворяет этим условиям,
то и не всякий ряд Тейлора сходится к
той функции, для которой он составлен.
именно к самой этой функции. Поскольку
не всякая бесконечно-дифференцируемая
функция, то есть такая функция, которой
можно поставить в соответствие ее ряд
Тейлора, удовлетворяет этим условиям,
то и не всякий ряд Тейлора сходится к
той функции, для которой он составлен.
Для сходимости
ряда Фурье во всех точках промежутка
![]() и для того, чтобы сумма ряда Фурье во
всем промежутке, за исключением лишь
конечного числа точек, совпадала с
функцией f(х),
породившей этот ряд Фурье, оказываются
достаточными, например, следующие
условия, наложенные на функцию f(х):
и для того, чтобы сумма ряда Фурье во
всем промежутке, за исключением лишь
конечного числа точек, совпадала с
функцией f(х),
породившей этот ряд Фурье, оказываются
достаточными, например, следующие
условия, наложенные на функцию f(х):
Т е о р е м а (Дирихле). Если функция f(х) такова, что
1) f(х) имеет в
![]() разве лишь конечное число точек разрыва
первого рода,
разве лишь конечное число точек разрыва
первого рода,
2) f(х) имеет
конечный правосторонний предел в точке
![]() и конечный левосторонний предел в точке
и конечный левосторонний предел в точке![]() ,
,
3) промежуток
![]() можно разбить на конечное число частей,
внутри каждой из которой f(х) изменяется
монотонно,
можно разбить на конечное число частей,
внутри каждой из которой f(х) изменяется
монотонно,
то ряд Фурье
функции f(х) сходится в промежутке
![]() ,
причем его сумма
,
причем его сумма
а) равна числу
![]() ,(1)
,(1)
если
![]() ,
,
б) равна числу
![]() ,(2)
,(2)
при
![]() и при
и при![]() .
.
Доказательство этой теоремы мы не приводим, так как оно требует довольно длительных и сложных рассуждений.
Замечание 1. Из а)
следует, что сумма ряда Фурье во всякой
точке
![]() ,
в которой f(х)
непрерывна, равна числу
,
в которой f(х)
непрерывна, равна числу
![]() .
Действительно, еслиf(х)
непрерывна в точке х0,
то
.
Действительно, еслиf(х)
непрерывна в точке х0,
то
![]() и значение выражения (1) совпадает со
значением
и значение выражения (1) совпадает со
значением![]() .
Следовательно, сумма ряда Фурье совпадает
с функцией
.
Следовательно, сумма ряда Фурье совпадает
с функцией![]() всюду, где
всюду, где![]() непрерывна.
непрерывна.
Замечание 2. Так
как члены ряда Фурье являются периодическими
функциями с периодом
![]() (как было указано в § 1), то из теоремы
Дирихле следует, что ряд Фурье при
указанных условиях сходится на всей
оси
(как было указано в § 1), то из теоремы
Дирихле следует, что ряд Фурье при
указанных условиях сходится на всей
оси![]() .
.
Замечание 3. Если
функция
![]() ,
для которой составляется ряд Фурье,
сама является периодической функцией
с периодом
,
для которой составляется ряд Фурье,
сама является периодической функцией
с периодом![]() (и удовлетворяет условиям теоремы
Дирихле), то утверждения а), б) и в) этой
теоремы справедливы не только в промежутке
(и удовлетворяет условиям теоремы
Дирихле), то утверждения а), б) и в) этой
теоремы справедливы не только в промежутке
![]() ,
но и в любом промежутке
,
но и в любом промежутке
![]() ,
где
,
где![]()
Таким образом, в
любой точке
![]() числовой оси, отличной от
числовой оси, отличной от![]() ,
сумма ряда Фурье равна значению выражения
(1) (если
,
сумма ряда Фурье равна значению выражения
(1) (если![]() непрерывна в точке
непрерывна в точке![]() ,
то значение (1) совпадает с
,
то значение (1) совпадает с![]() );
в точках вида
);
в точках вида![]() сумма ряда Фурье равна значению выражения
(2).
сумма ряда Фурье равна значению выражения
(2).