Файл: trigonometrich_ryad.doc

6. Разложение функции, заданной в промежутке [0,π], в тригонометрический ряд

Пусть функция задана в промежуткеи на этом промежутке удовлетворяет условиям Дирихле. Её нельзя разложить в ряд Фурье с помощью формул (1) из § 2, так как эти формулы для коэффициентов Фурье предполагают, что функция задана в . Поэтому нужно доопределить функцию каким-нибудь образом в промежутке . Такое доопределение функции желательно делать, если это возможно, так, чтобы продолженная на весь промежуток функция удовлетворяла требованиям теоремы Дирихле. Очевидно, что продолжить заданную функцию таким образом на можно бесчисленным множеством способов. На рисунке 115 показано, например, пять разных способов продолжения функции на, не противоречащих требованиям теоремы Дирихле (график данной функции внарисован жирной сплошной линией, а ее продолжения нанарисованы различными пунктирными линиями или тонкими сплошными линиями).

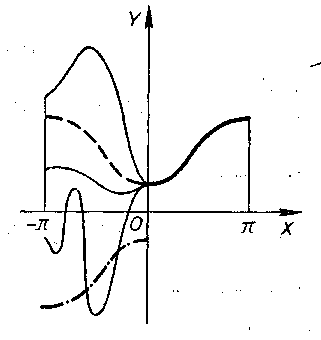
Обозначим через функцию, которая насовпадает с заданной функцией, а наявляется каким-нибудь продолжением функции. Как указывалось выше, таких функцийможно построить, исходя из заданной функции, бесчисленное множество. Все они определены в и удовлетворяют требованиям теоремы Дирихле. Поэтому каждую такую функцию можно по теореме Дирихле разложить в ряд Фурье:

---

(1)

и это разложение справедливо в , за исключением, может быть, конечного числа точек, являющихся точками разрыва функции.

Так как на имеет место равенство=, то разложение (1) дает дляразложение исходной функциив тригонометрический ряд:

(2)

(Этот тригонометрический ряд нельзя назвать рядом Фурье для , так как, как указывалось в начале параграфа, само понятие ряда Фурье неприменимо к функции, заданной на. Числаявляются коэффициентами Фурье функции, но в равенстве (2) их следует рассматривать лишь как числовые коэффициенты некоторого тригонометрического ряда).

Коэффициенты иряда Фурье (1) функцииразличны для различных функций, то есть, иначе говоря, при различных способах продолжения исходной функциимы получим разные ряды (1) и, следовательно, формула (2) дает для исходной функциибесконечное множество разложений в разные тригонометрические ряды. Среди всех возможных продолжений функциинаможно выделить «четное продолжение», то есть такое, при котором функцияоказывается четной в (на рис. 115 оно обозначено простым пунктиром), и «нечетное продолжение», то есть такое, при котором функция оказывается нечетной в (на рис. 115 оно обозначено пунктиром «тире – точка – тире»). При четном продолжении получаем ряд Фурье (1) функции , содержащий только косинусы (см. § 3, пункт 1), и, следовательно, получаем разложениев тригонометрический ряд (2) втолько по косинусам. При нечетном продолжении получаем ряд Фурье (1) для функции, содержащий только синусы (см. § 3, пункт 2), и, следовательно, получаем разложение той же исходной функциив тригонометрический ряд (2) втолько по синусам.

---

На практике при разложении функции , заданной на, в тригонометрический ряд только по косинусам или только по синусам нет необходимости фактически осуществлять ее продолжение на. Ведь после продолжения мы должны воспользоваться формулами (2) или соответственно (4) из § 3, а в этих формулах участвуют интегралы только от 0 до π, то есть по тому промежутку, где=. Способ продолжения играет роль только при подсчете, чему равны суммы полученного ряда в точкахх = 0 и х = π.

Рассмотрим несколько примеров разложения функции, заданной в , в тригонометрический ряд.

Пример 1. зададим функцию в промежутке равенствоми поставим задачу: разложить эту функцию вв тригонометрический ряд по косинусам. Для этого на основании изложенного выше надо вычислить коэффициенты такого разложения по формулам:

;

(см. выкладки из примера 3 в § 4);

Таким образом, разложение функции в ряд по косинусам имеет вид:

(3)

Для того чтобы найти сумму этого ряда в точках х = 0 и х = π, надо вычислить числа (2) из § 4 для функции , которая является четным продолжением заданной функции на промежуток. Так как при четном продолжении продолженная функциянепрерывна прих = 0, то сумма ее ряда Фурье (3) равна 0 в точке х = 0.

---

При х = π имеем:

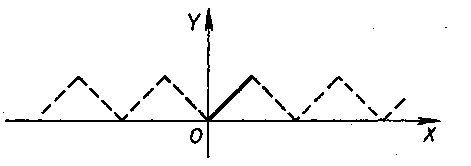
Следовательно, разложение (3) справедливо для . На рисунке116 пунктиром изображен график суммы ряда (3) вне промежутка.

В примере 1 из § 4 была разложена в ряд Фурье нечетная функция

= х в ( см. (3) из § 4). Это разложение справедливо, в частности, и в промежутке ; поэтому его можно рассматривать как разложение в тригонометрический ряд по синусам в промежутке функции.

В примере 3 из § 4 функция, заданная в равенствами (8), может тоже рассматриваться как одно из возможных продолжений функции , заданной только в. Тогда равенство (9) из § 4, которое справедливо также и в, можно записать в виде

x = ,< (4)

---

и рассматривать его как одно из возможных разложений функции вв тригонометрический ряд.

Таким образом, для функции мы получили втри разных разложения в тригонометрический ряд: (3) и (4) из данного параграфа и (3) из § 4.

Пример 2. Зададим функцию в равенством и поставим задачу: разложить эту функцию в промежутке в тригонометрический ряд по синусам.

Для этого надо вычислить коэффициент по формулам:

(n=0, 1, 2, …)

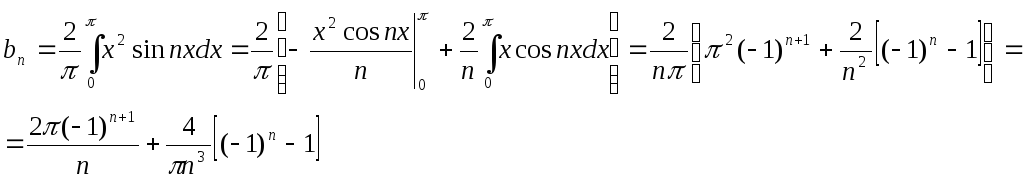
Таким образом, функция раскладывается в следующий ряд по синусам:

(5)

Так как функция непрерывная и монотонно возрастающая в , то разложение (5) справедливо в. Найдем сумму ряда (5) прии при. Ввиду того что требовалось разложить в ряд по синусам, мы продолжим ее на нечетно, но так как, то разрыва в начале координат при нечетном продолжении не получается, и поэтому равенство (5) справедливо и при. Находим значение суммы ряда (5) при:

---