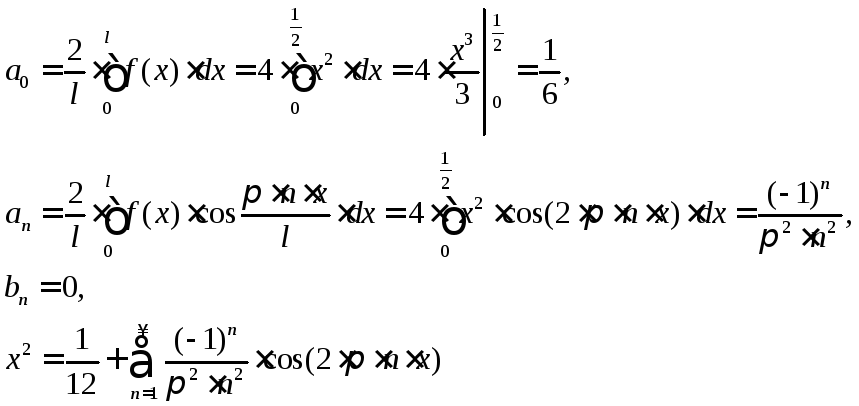ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 17.04.2024
Просмотров: 97
Скачиваний: 0
![]()
Следовательно,
при
![]() значение суммы ряда (5) не совпадает со
значением
значение суммы ряда (5) не совпадает со
значением![]() ,
и поэтому разложение (5) справедливо в
промежутке
,
и поэтому разложение (5) справедливо в
промежутке![]() .
.
На рисунке пунктиром
изображен график суммы ряда вне промежутка
![]() .
.
В примере 2 из § 4
было получено разложение четной функции
![]() в
в![]() в ряд Фурье по косинусам (см. (4) из § 4).
Это же разложение можно рассматривать
в
в ряд Фурье по косинусам (см. (4) из § 4).
Это же разложение можно рассматривать
в![]() ,
и там оно будет давать разложение в
тригонометрический ряд по косинусам
функции
,
и там оно будет давать разложение в
тригонометрический ряд по косинусам
функции![]() ,
заданной в
,
заданной в![]() .
.
Разложить в ряд
по косинусам функцию
![]() в
в![]() .
.
Чтобы это сделать,
продолжим её на весь отрезок![]() чётным образом и найдём коэффициенты
чётным образом и найдём коэффициенты
![]()
![]() ;
;
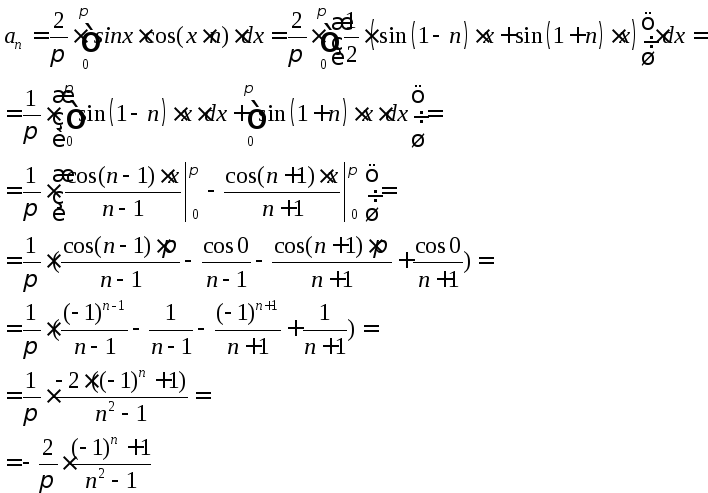
![]()
При
![]() :
:

7. Разложение в тригонометрический ряд функции, заданной в промежутке
Пусть функция
![]() задана в промежутке
задана в промежутке![]() ,
гдеl
– произвольное положительное
число, и удовлетворяет там условиям
теоремы Дирихле из § 4.
,
гдеl
– произвольное положительное
число, и удовлетворяет там условиям
теоремы Дирихле из § 4.
Введем новую
переменную
![]() по формуле:
по формуле:
![]() .
(1)
.
(1)
Из формулы (1) видно,
что, когда переменная x,
возрастает, пробегает промежуток
![]() ,
переменная
,
переменная![]() ,
также возрастая, пробегает промежуток
,
также возрастая, пробегает промежуток![]() .
.
Обозначим через
![]() ту функцию, в которую преобразуется
ту функцию, в которую преобразуется![]() при замене переменной по формуле (1), то
есть положим
при замене переменной по формуле (1), то
есть положим![]() .
(2)
.
(2)
Функция
![]() определена в промежутке
определена в промежутке![]() и удовлетворяет в нем условиям Дирихле,
так как замена переменнойx
новой переменной, связанной линейно с
x
(см. (1)), не может привести к нарушению
требований теоремы Дирихле.
и удовлетворяет в нем условиям Дирихле,
так как замена переменнойx
новой переменной, связанной линейно с
x
(см. (1)), не может привести к нарушению
требований теоремы Дирихле.
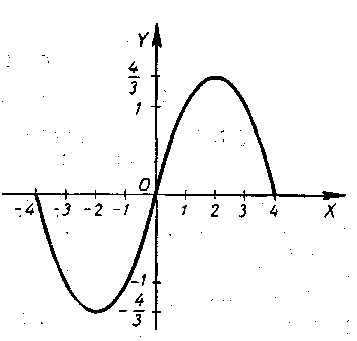
В соответствии с
утверждением теоремы Дирихле разложим
функцию
![]() в
в![]() в ряд Фурье:
в ряд Фурье:
![]() (3)
(3)
где
![]() ,
,![]() и
и![]() определятся по обычным формулам:
определятся по обычным формулам:
![]() ,
,
![]() ,
,![]() (4)
(4)
Вернемся теперь
от переменной
![]() обратно к переменнойx;
из (1) находим
обратно к переменнойx;
из (1) находим
![]() и подставляем это выражение
и подставляем это выражение![]() в (3).
в (3).
Тогда получаем, используя (2):
![]() ,
(5)
,
(5)
где
![]() .
.
Формулы (4) для коэффициентов принимают следующий вид:
![]()
![]()
![]() (6)
(6)
На разложение вида
(5) можно перенести результаты, изложенные
в §3, 5 и 6. Так, например, при разложении
функции
![]() в
в![]() в ряд по синусам получаем:
в ряд по синусам получаем:
![]() (7)
(7)
где
![]() (8)
(8)
Пример. Разложим
в тригонометрический ряд в промежутке
![]() функцию
функцию
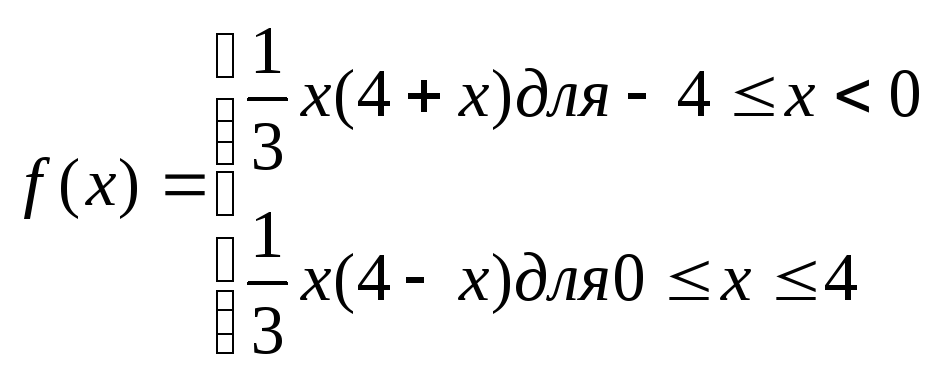 (9)
(9)
Эта функция
непрерывная и нечетная в промежутке
![]() ;
её график изображен на рисунке 118.
Действительно, если во второй строчке
формулы (9) заменитьx
на –x,
то получим
;
её график изображен на рисунке 118.
Действительно, если во второй строчке
формулы (9) заменитьx
на –x,
то получим
![]() ,
то есть получим выражение, только знаком
отличающееся от того выражения, которым
функция задана на
,
то есть получим выражение, только знаком
отличающееся от того выражения, которым
функция задана на![]() .
Функция (9)удовлетворяет условиям теоремы
Дирихле в
.
Функция (9)удовлетворяет условиям теоремы
Дирихле в![]() .
Следовательно ее можно разложить в ряд,
причем получим (см. (7) и (8)):
.
Следовательно ее можно разложить в ряд,
причем получим (см. (7) и (8)):
![]() n=(0,
1, 2, 3, …) и
n=(0,
1, 2, 3, …) и
![]() .
.
Вычисляя этот интеграл, находим:
![]() (10)
(10)
Значение функции
(9) при
![]() равно нулю, и значения суммы ряда с
коэффициентами (10) также равны нулю:
равно нулю, и значения суммы ряда с
коэффициентами (10) также равны нулю:![]() .
Таким образом, разложение
.
Таким образом, разложение
![]()
справедливо в
промежутке
![]() .
.
Пример
№1Разложить в
тригонометрический ряд
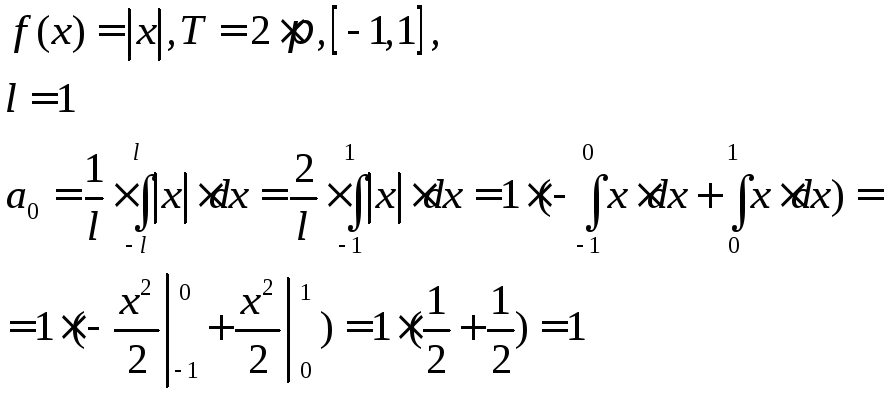
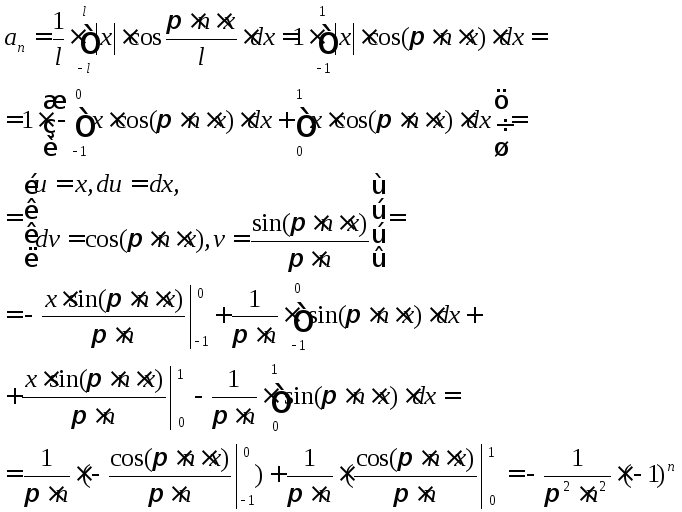

№2
![]()
![]() на
на
![]()
![]() ,
,![]()