Файл: trigonometrich_ryad.doc

Замечание 4. Если функция , для которой составляется ряд Фурье, задана на всей оси и непериодическая, то за пределами промежутка утверждения теоремы Дирихле уже не имеют места. Непериодическая функция и периодическая функция – сумма ряда Фурье – не имеют ничего общего за пределами промежутка . Это наглядно можно проследить на рассматриваемых ниже примерах (см. рис. 112 и 113).

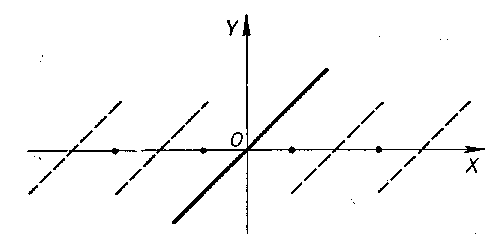
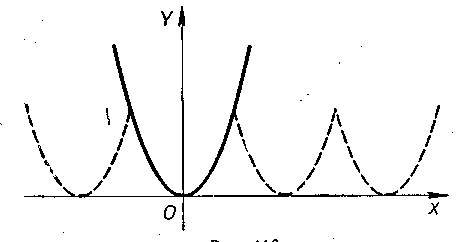
Пример 1. Рассмотрим функцию . Она нечетная и, очевидно, удовлетворяет условиям теоремы Дирихле. Вычислим ее коэффициенты Фурье (см. формулы (3) и (4) из § 3):,

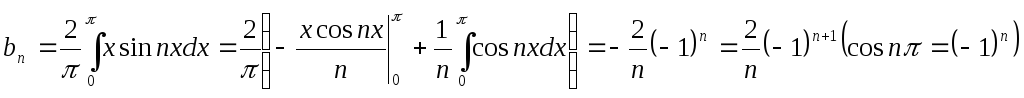
Так как функция непрерывна в , то сумма ряда Фурье совпадает с в , то есть можно написать, используя найденные коэффициенты Фурье:

(3)

причем это равенство справедливо для . В точкахсумма ряда Фурье по теореме Дирихле определяется выражением (2):

Впрочем, непосредственно видно, что все члены ряда (3) равны нулю при , и поэтому сумма ряда равна нулю.

---

Таким образом, в этих двух точках значения суммы ряда Фурье не совпадают со значениями функции . Вне промежутка сумма ряда Фурье дает периодическое продолжение своего графика в , что на рисунке 112 отмечено пунктирными линиями; график же функции продолжен вне сплошной линией, и видно, что эти два графика, совпадающие в , не имеют ни одной общей точки вне .

Пример 2. Рассмотрим функцию . Она четная и удовлетворяет условиям теоремы Дирихле. Вычислим ее коэффициенты Фурье (см. формулы (1) и (2) из § 3):

; ;

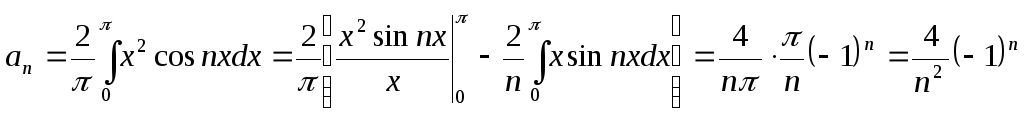
(при вычислении второго слагаемого в квадратных скобках был использован результат вычислений из примера 1).

Так как функция непрерывна в , то сумма ряда Фурье совпадает с ней во всех точках . Вычислим значение выражения (2):

Оно совпадает со значениями функции в точках, и, следовательно, сумма ряда Фурье совпадает с функциейдля всех:

(4)

---

Вне промежутка сумма ряда Фурье и функция и на этот раз не имеют ничего общего (см. рис.113, на котором график функциипомечен сплошной линией, а график суммы ряда Фурье вне – пунктирной линией).

Замечание. Разложение (4) можно использовать для нахождения сумм некоторых числовых рядов.

а) Положим в (4) ; тогда получим:

, или , откуда находим:

, то есть (5)

б) Положим теперь в (4) , тогда

Отсюда находим сумму следующего числового ряда:

, то есть (6)

в) Очевидно, что

Отсюда, используя (5), находим:

, то есть (7)

г) Непосредственно из (5) получаем:

, то есть

Пример 3. Разложить в ряд Фурье функцию, заданную на промежутке следующим образом:

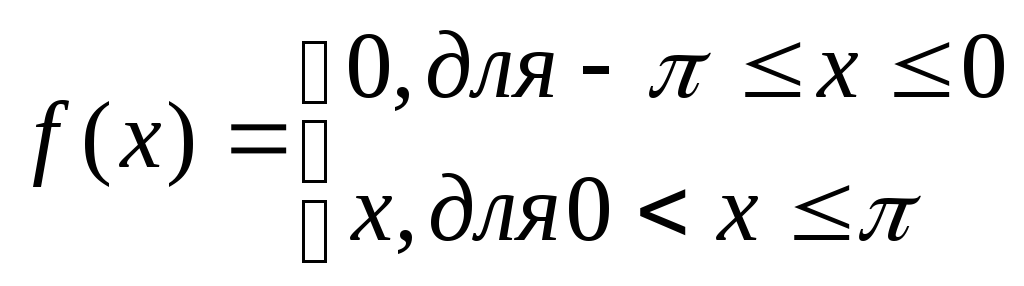(8)

Эта функция непрерывна и монотонно возрастает (в широком смысле слова) в . Следовательно, по теореме Дирихле она разлагается в ряд Фурье в . Найдем ее коэффициенты Фурье по формулам (1) из § 2. Вследствие того что функция задана разными формулами наи, приходится для вычисления интегралов по разбивать их на два интеграла – по и по:

---

;

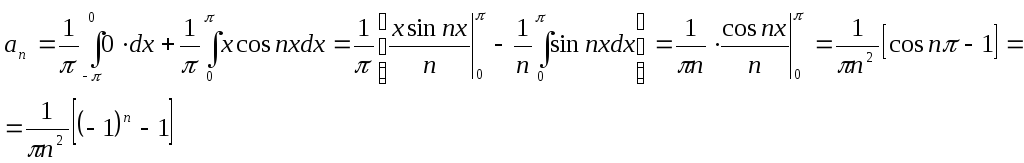
(отсюда видно, что при четныхп и при нечетныхп);

(см. выкладки из примера 1).

Найдем значение выражения (2):

Это число не совпадает со значениями функции в точках(см.(8)), следовательно, равенство

(9)

справедливо только для . На рисунке 114 изображен график суммы ряда Фурье для функции (8).

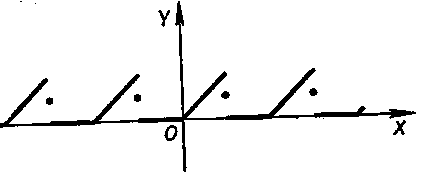
На этом примере видно, что функция, которая в двух разных половинах промежутка задавалась двумя разными аналитическими выражениями, может представляться во всем единым тригонометрическим рядом (9). Аналогичные факты можно проследить и дальше в § 5 и 6 и в упражнениях к § 4,5.

Пример:

Функция -нечётная, на.Вычислим её коэффициенты Фурье:

---

Сумма ряда равна 0. Таким образом, в точках значение суммы ряда Фурье не совпадают со значениями функции.

---