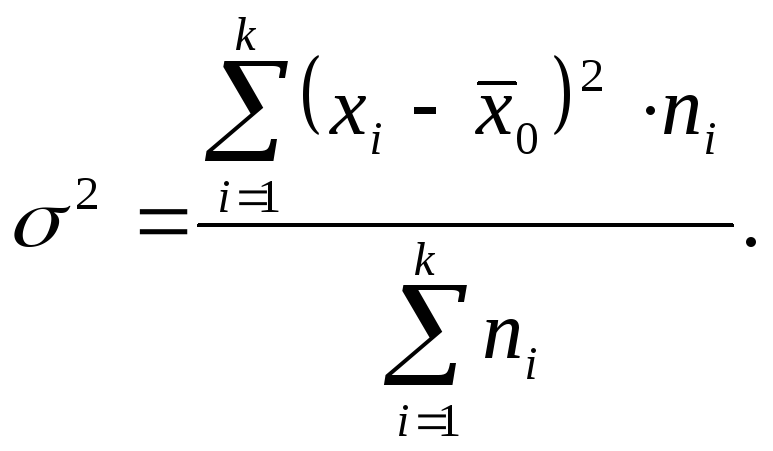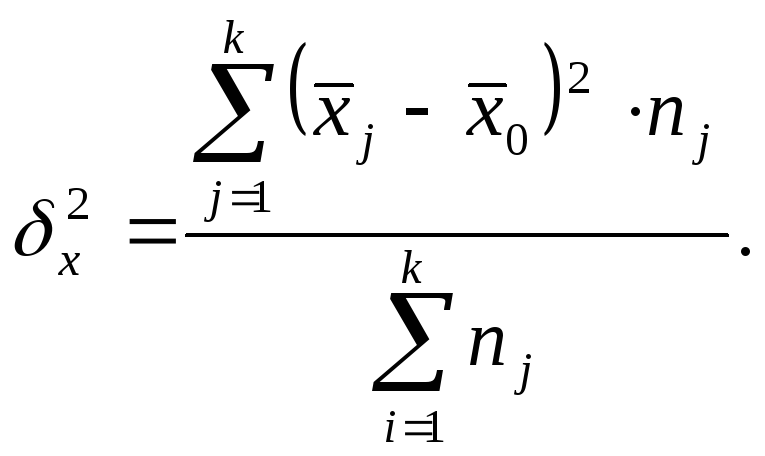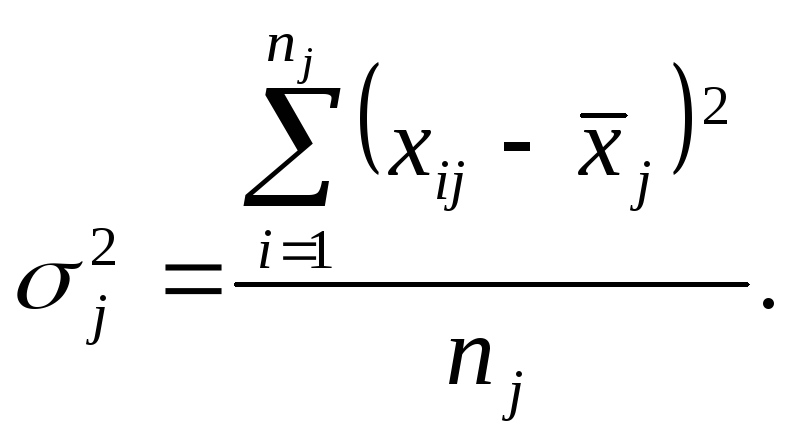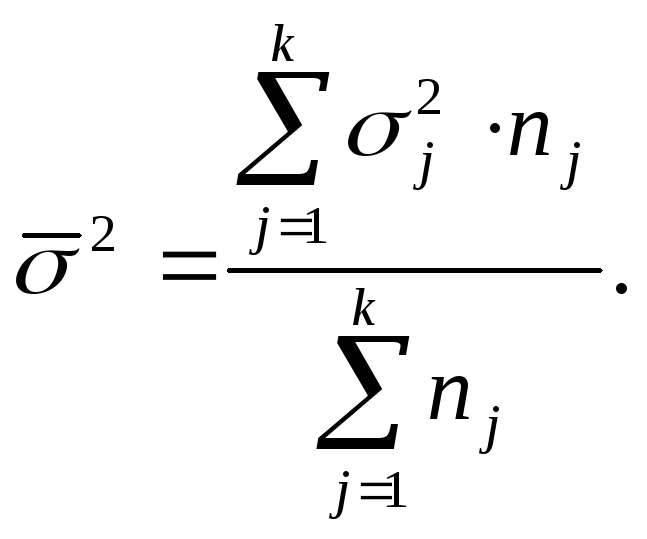ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 02.08.2024
Просмотров: 126
Скачиваний: 0
СОДЕРЖАНИЕ
Тема 7 показатели вариации и анализ частотных распределений
Вариация признака в совокупности и значение ее изучения
7.2 Показатели центрараспределения
7.3 Показатели вариации и способы их расчета
7.4 Вариации альтернативного признака. Энтропия распределения
7.5 Виды дисперсий в совокупности, разделенной на группы. Правило сложения дисперсий
7.6 Структурные характеристики вариационного ряда распределения. Показатели дифференциации
7.8 Изучение формы распределения
7.9 Теоретические распределения в анализе вариационных рядов
7.4 Вариации альтернативного признака. Энтропия распределения
В ряде случаев возникает необходимость в измерении дисперсии так называемых альтернативных признаков, тех, которыми обладают одни единицы совокупности и не обладают другие. Примером таких признаков являются: бракованная продукция, ученая степень преподавателя вуза, работа по полученной специальности и т.д. Вариация альтернативного признака количественно проявляется в значении нуля у единицы, которая этим признаком не обладает, или единицы у той, которая данный признак имеет.
Пусть
![]() - доля единиц в совокупности, обладающих
данным признаком
- доля единиц в совокупности, обладающих
данным признаком![]() ;
;
![]() - доля единиц, не обладающих данным
признаком, причем
- доля единиц, не обладающих данным
признаком, причем![]() .
Альтернативный признак принимает всего
два значения - 0 и 1 с весами соответственно
.
Альтернативный признак принимает всего
два значения - 0 и 1 с весами соответственно![]() и
и![]() .
Исчислим среднее значение альтернативного
признака по формуле средней арифметической:
.
Исчислим среднее значение альтернативного
признака по формуле средней арифметической:
|
|
(7.30) |
Дисперсия альтернативного признака определяется по формуле:
|
|
(7.31) |
Таким образом, дисперсия альтернативного
признака равна произведению доли на
число, дополняющее эту долю до единицы.
Корень квадратный из этого показателя,
т.е.
![]() ,
соответствует среднему квадратическому
отклонению альтернативного признака.
Предельное значение дисперсии
альтернативного признака равно 0,25 при
,
соответствует среднему квадратическому
отклонению альтернативного признака.
Предельное значение дисперсии
альтернативного признака равно 0,25 при![]() .
.
Показатели вариации альтернативных признаков широко используются в статистике, в частности, при проектировании выборочного наблюдения, обработке данных социологических обследований, статистическом контроле качества продукции, в ряде других случаев.
Обобщенной характеристикой различий внутри ряда может служить энтропия распределения. Применительно к статистике энтропия - это мера неопределенности данных наблюдения, которая может иметь различные результаты. Энтропия зависит от числа градаций признака и от вероятности каждой из них. Энтропия показывает, имеется ли закономерность в концентрации отдельных градаций у наименьшего числа позиций или, напротив, заполненность распределения одинаковая. При этом сумма вероятностей всех возможных исходов равна единице. Энтропия измеряется в битах.
Показатель энтропии
![]() представляет собой отрицательную
сумму произведения вероятностей
различных значений случайной величины
(
представляет собой отрицательную
сумму произведения вероятностей
различных значений случайной величины
(![]() )
на логарифмы (при основании два) этих
вероятностей:
)
на логарифмы (при основании два) этих
вероятностей:
|
|
(7.32) |
Если все варианты равновероятны, то энтропия максимальна. Если же все варианты, за исключением одного, равны нулю, то энтропия равна нулю.
Энтропия альтернативного признака (![]() )
при равновероятном распределении (
)
при равновероятном распределении (![]() )
равна единице:
)
равна единице:
|
|
(7.33) |
Энтропия сложной системы вычисляется следующим образом:
|
|
(7.34) |
где
![]() - вероятность любого возможного состояния
сложной системы.
- вероятность любого возможного состояния
сложной системы.
Показатель энтропии позволяет также
измерять количество информации. Чем
больше информации о случайном событии,
тем определеннее его состояние. Чем
больше вероятность случайного события
![]() ,
тем меньше информации несет его
осуществление. В случае
,
тем меньше информации несет его
осуществление. В случае![]() .
.
|
|
(7.35) |
Следовательно, данное испытание не
содержит никакой информации. Аналогично
и при
![]() .
.
Энтропия распределения интерпретируется как мера рассредоточенности вариантов случайной переменной по ее возможным значениям, или как мера неопределенности значения реализации. Неопределенность значений реализации случайной переменной предусматривает наличие некоторого наблюдателя, находящегося в том или ином отношении к источнику неопределенности. Очевидно, можно представить ситуацию, когда для двух наблюдений степени неопределенности результата одного и того же наблюдения со случайными исходами существенно различаются. Например, различны результаты голосования при экспертных опросах для наблюдателя - участника голосования и наблюдателя, не участвующего в голосовании.
В связи с тем что верхнего предела энтропия распределения не имеет, целесообразно вычислить наряду с абсолютной и относительную величину неопределенности.
Относительная энтропия определяется как отношение ее фактической величины к максимальной, т.е.
|
|
(7.36) |
Это отношение изменяется от 0 до 1 и может быть интерпретировано. Чем меньше относительная энтропия, тем меньше неопределенность и выше однородность.
7.5 Виды дисперсий в совокупности, разделенной на группы. Правило сложения дисперсий
Изучая вариацию по всей совокупности в целом и опираясь на общую среднюю в своих расчетах, мы не можем определить влияние отдельных факторов, характеризующих колеблемость индивидуальных значений признака. Это можно сделать при помощи аналитической группировки, разделив изучаемую совокупность на однородные группы по признаку-фактору. При этом можно определить три показателя колеблемости признака в совокупности: дисперсию общую, межгрупповую и среднюю из внутригрупповых дисперсий.
Общая дисперсия ![]() измеряет вариацию признака во всей
совокупности под влиянием всех факторов,
обусловивших эту вариацию:
измеряет вариацию признака во всей
совокупности под влиянием всех факторов,
обусловивших эту вариацию:
|
|
(7.37) |
Межгрупповая дисперсия (![]() )
характеризует систематическую вариацию,
т.е. различия в величине изучаемого
признака, возникающие под влиянием
признака-фактора, положенного в основание
группировки. Она рассчитывается по
формуле
)
характеризует систематическую вариацию,
т.е. различия в величине изучаемого
признака, возникающие под влиянием
признака-фактора, положенного в основание
группировки. Она рассчитывается по
формуле
|
|
(7.38) |
где
![]() - число групп;
- число групп;
![]() - число единиц в
- число единиц в![]() -й
группе;
-й
группе;
![]() - частная средняя по
- частная средняя по![]() -й
группе;
-й
группе;
![]() - общая средняя по совокупности единиц.
- общая средняя по совокупности единиц.
Внутригрупповая дисперсия (![]() )
отражает случайную вариацию, т.е. часть
вариации, происходящую под влиянием
неучтенных факторов и не зависящую от
признака-фактора, положенного в основание
группировки. Она исчисляется следующим
образом:
)
отражает случайную вариацию, т.е. часть
вариации, происходящую под влиянием
неучтенных факторов и не зависящую от
признака-фактора, положенного в основание
группировки. Она исчисляется следующим
образом:
|
|
(7.39) |
По совокупности в целом вариация значений
признака под влиянием прочих факторов
характеризуется средней из внутригрупповых
дисперсий (![]() ):
):
|
|
(7.40) |
Между общей дисперсией
![]() ,
средней из внутригрупповых дисперсий
,
средней из внутригрупповых дисперсий![]() и межгрупповой
и межгрупповой![]() дисперсией существует соотношение,
определяемоеправилом сложения
дисперсий. Согласно этому правилуобщая дисперсия равна сумме средней
из внутригрупповых и межгрупповой
дисперсий:
дисперсией существует соотношение,
определяемоеправилом сложения
дисперсий. Согласно этому правилуобщая дисперсия равна сумме средней
из внутригрупповых и межгрупповой
дисперсий:
|
|
(7.41) |
Согласно этому правилу, общая дисперсия, возникающая под действием всех факторов, равна сумме дисперсий, появляющихся под влиянием всех прочих факторов, и дисперсии, возникающей за счет группировочного признака.
Зная любые два вида дисперсий, можно определить или проверить правильность расчета третьего вида.
Правило сложения дисперсий позволяет
выявить зависимость результата от
определяющих факторов с помощью
соотношения межгрупповой дисперсии и
общей дисперсии. Это соотношение
называется эмпирическим коэффициентом
детерминации (![]() ):
):
|
|
(7.42) |
Он показывает, какая доля в общей дисперсии приходится на дисперсию, обусловленную вариацией признака, положенного в основу группировки.
Корень квадратный из эмпирического
коэффициента детерминации носит название
эмпирического корреляционного
отношения (![]() ):
):