ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 17.08.2024
Просмотров: 42
Скачиваний: 0
СОДЕРЖАНИЕ
§2. Свойства функций, заданных в евклидовом пространстве.
§3. Частные производные функции нескольких переменных.
§3. Понятие дифференцируемости функции нескольких переменных.
Геометрический смысл полного дифференциала.
§5. Производная по направлению, градиент функции.
§6.Частные производные высших порядков.
§7. Экстремумы функции нескольких переменных
Теорема 1 (необходимый признак экстремума функции многих переменных):
Геометрический смысл полного дифференциала.
Для функции одной переменной y = f(x)в точкеx0 геометрический смысл дифференциала означает приращение ординаты касательной, проведенной к графику функции в точке с абсциссойx0при переходе к точкеx0 + x. А дифференциал функции двух переменных в этом плане является приращениемаппликатыкасательнойплоскости, проведенной к поверхности, заданной уравнениемz = f(x,y), в точкеM0(x0, y0) при переходе к точкеM(x0 + x, y0 + y).Дадим определение касательной плоскости к некоторой поверхности:
Df.Плоскость, проходящая через точкуР0поверхностиS, называетсякасательной плоскостью в данной точке, если угол между этой плоскостью и секущей, проходящей через две точкиР0иР(любая точка поверхностиS), стремится к нулю, когда точкаРстремится по этой поверхности к точкеР0.
Пусть поверхность Sзадана уравнениемz = f(x,y).Тогда можно показать, что эта поверхность имеет в точкеP0(x0, y0, z0)касательную плоскость тогда и только тогда, если функцияz = f(x,y)дифференцируема в этой точке. В этом случае касательная плоскость задается уравнением:
z – z0
=
![]() +
+
![]() (6).
(6).
§5. Производная по направлению, градиент функции.
Частные производные функции y=f(x1,x2..xn)по переменнымx1,
x2 . . . xn
выражают скорость изменения функции
по направлению координатных осей.
Например,![]() есть скорость изменения функции пох1
– то есть предполагается , что точка,
принадлежащая области определения
функции, перемещается лишь параллельно
осиОХ1, а все
остальные координаты остаются неизменными.
Однако, можно предположить, что функция
может изменяться и по какому-нибудь
другому направлению, не совпадающему
с направлением какой либо из осей.
есть скорость изменения функции пох1
– то есть предполагается , что точка,
принадлежащая области определения
функции, перемещается лишь параллельно
осиОХ1, а все
остальные координаты остаются неизменными.
Однако, можно предположить, что функция
может изменяться и по какому-нибудь
другому направлению, не совпадающему
с направлением какой либо из осей.
Рассмотрим функцию трех переменных: u=f(x,y,z).
Зафиксируем точку М0(x0,y0,z0)и какую-нибудь направленную прямую (ось)l, проходящую через эту точку. ПустьМ(x,y,z) - произвольная точка этой прямой иМ0М- расстояние отМ0доМ.
u = f (x,y,z) – f(x0,y0,z0)– приращение функции в точкеМ0.
Найдем отношение приращения функции к
длине вектора
![]() :
:
![]()
Df.Производной функцииu = f (x,y,z)по направлениюl в точкеМ0называется предел отношения приращения функции к длине вектораМ0Мпри стремлении последнего к 0 (или, что одно и то же, при неограниченном приближенииМкМ0):
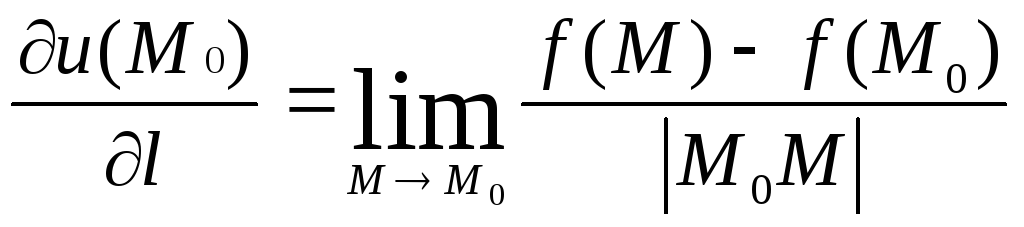 (1)
(1)
Эта производная характеризует скорость изменения функции в точке М0в направленииl.
Пусть ось l (векторМ0М) образует с
осямиOX, OY,
OZуглы![]() соответственно.
соответственно.
Обозначим x-x0=
![]() ;
;
y - y0
=
![]() ;
;
z - z0
=
![]() .
.
Тогда вектор М0М = (x
- x0, y
- y0, z
- z0)=
![]() и
его направляющие косинусы:
и
его направляющие косинусы:
![]() ;
;
![]() ;
;
![]() .
.
![]() (4).
(4).
(4) – формула для вычисления производной по направлению.
Рассмотрим вектор, координатами которого являются частные производные функции u=f(x, y, z)в точкеМ0:
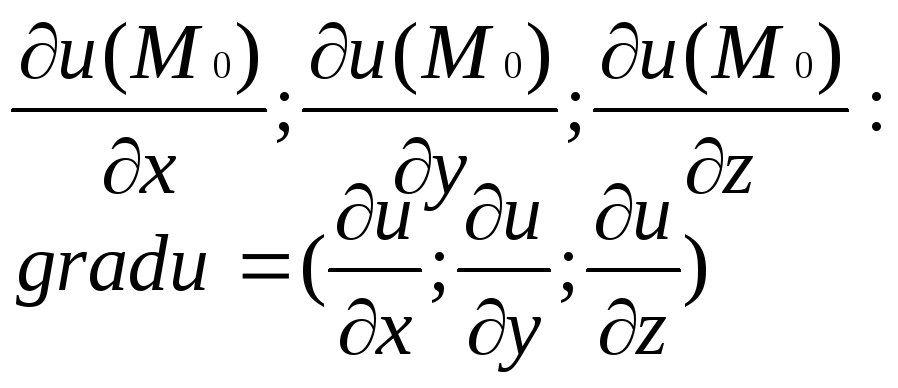
grad u - градиент функцииu=f(x, y, z)в точке М(x, y, z)
Свойства градиента:
Производная функции u=f(x, y, z)в данной точке М(x, y, z)по направлениюlимеет наибольшее значение, если направлениеlсовпадает с направлением градиента функции в этой точке.
Наибольшее значение производной функции u=f(x, y, z)по заданному направлению в данной точкеМ(x, y, z) равно длине градиента функции в этой точке:
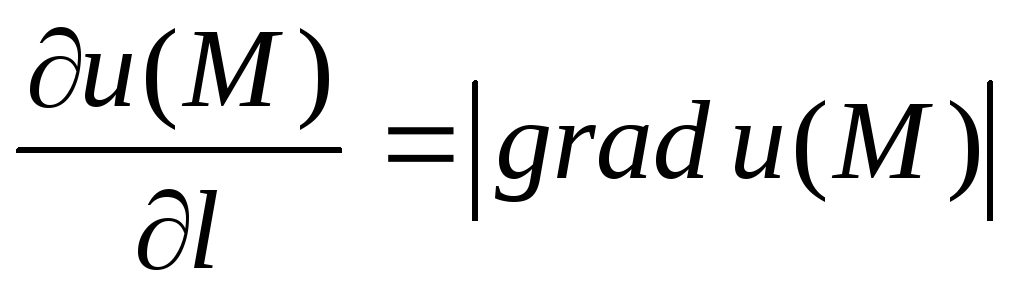 .
.
Вывод: длина градиента функцииu=f(x,
y, z) – есть наиболее возможное значение![]()
![]() в данной точкеМ(x,
y, z),
а направление вектораgrad
uсовпадает с
направлением вектора, выходящего из
точкиМ, вдоль которого функция
меняется быстрее всего. То есть,
направление градиента функции grad
u - есть направление
наискорейшего возрастания функции.
в данной точкеМ(x,
y, z),
а направление вектораgrad
uсовпадает с
направлением вектора, выходящего из
точкиМ, вдоль которого функция
меняется быстрее всего. То есть,
направление градиента функции grad
u - есть направление
наискорейшего возрастания функции.
§6.Частные производные высших порядков.
Частные производные
![]() ,i = 1,2, . . . ,nназываютчастными производными
первого порядка.Их можно
рассматривать как функции отX=(x1,x2,.
. . xn)
,i = 1,2, . . . ,nназываютчастными производными
первого порядка.Их можно
рассматривать как функции отX=(x1,x2,.
. . xn)![]() .
Эти функции могут иметь частные
производные, которые называютсячастными
производными второго порядка. Они
определяются и обозначаются следующим
образом:
.
Эти функции могут иметь частные
производные, которые называютсячастными
производными второго порядка. Они
определяются и обозначаются следующим
образом:
![]() (1),
(1),
где i = 1, 2, . . . , n иk = 1, 2, . . . , n.
Если i k, то частная производная (1) называетсясмешанной частной производной второго порядка. Еслиi = k, то частная производная второго порядка обозначается следующим образом:
![]() (2).
(2).
Аналогично определяются частные производные третьего, четвертого и т.д. порядков.
Функция y = f (x1,x2…xn)называетсяm раз дифференцируемой в точкеМ0(x10, x20. . . ,xn0),если все её частные производные(m-1)-го порядка являются дифференцируемыми функциями в этой точке.
Теорема Шварца
Если функция y = f (X) дифференцируема m раз в точке M (x1, x2 .. xn), то смешанные производные m- го порядка в этой точке, отличающиеся лишь порядком дифференцирования, равны между собой.
В частности, для функции z
= f (x,y)имеем![]() .
.
§7. Экстремумы функции нескольких переменных
п.1 Определение и необходимые условия локального экстремума
Пусть функция y = f
(X)определена на некотором множестве![]() ,
аM0
(x10,x20
.. xn0)– некоторая точка этого множества.
,
аM0
(x10,x20
.. xn0)– некоторая точка этого множества.
Df.1
Функция y = f(X)
имеет в точке М0 локальный
максимум (минимум), если существует
такая окрестность точки М0
![]() ,что для любой точки М(x1,x2
.. xn)
из этой окрестности выполняется
неравенство
,что для любой точки М(x1,x2
.. xn)
из этой окрестности выполняется
неравенство
![]() .
.
Так же, как и в случае функции одной переменной,точка М0 называется критической точкой функцииy = f(X), если все частные производные функции в этой точке равны нулю или какая-нибудь из них не существует.Точка М0 называется стационарной точкойфункции, если она есть внутренняя точка области определения и все частные производные функции в этой точке равны нулю.
Теорема 1 (необходимый признак экстремума функции многих переменных):
Если функция y = f(x1, x2, . . . ,xn) имеет во внутренней точке М0(x10,x20.. xn0) экстремум и частные производные первого порядка, то все эти частные производные равны нулю в точке М0:
![]()
Итак, «подозрительными» на экстремум являются те точки, в которых все частные производные равны нулю или какая-нибудь из них не существует; в случае, если функция всюду имеет частные производные, то координаты этих точек можно найти, решив систему уравнений:
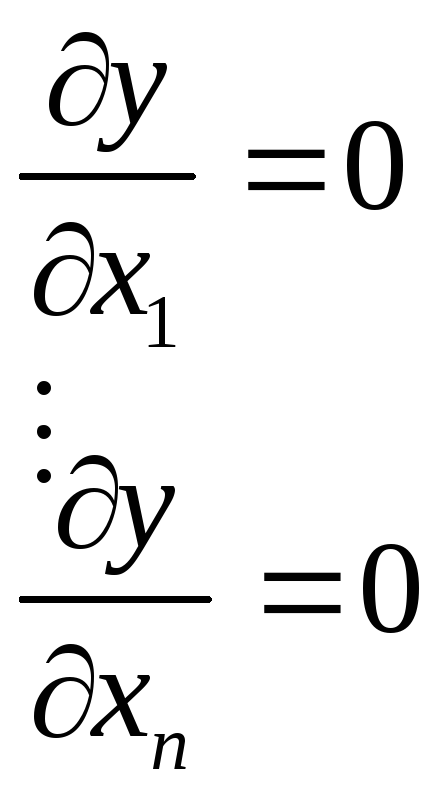
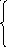 (2).
(2).
п.2 Достаточное условие экстремума
Для функции многих переменных достаточный признак экстремума намного более сложен, чем для функции одной переменной (Если в точке х = х0: f(x0)=0, тогда еслиf”(x0) < 0то в этой точке функция имеет максимум, а если f”(x0) > 0то - минимум).
Ограничимся случаем функции двух переменных: