ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 17.08.2024
Просмотров: 39
Скачиваний: 0
СОДЕРЖАНИЕ
§2. Свойства функций, заданных в евклидовом пространстве.
§3. Частные производные функции нескольких переменных.
§3. Понятие дифференцируемости функции нескольких переменных.
Геометрический смысл полного дифференциала.
§5. Производная по направлению, градиент функции.
§6.Частные производные высших порядков.
§7. Экстремумы функции нескольких переменных
Теорема 1 (необходимый признак экстремума функции многих переменных):
ТЕМА: ФУНКЦИИ НЕСКОЛЬКИХ
Теоретический материал для изучения
§1. Основные понятия.
Приведем примеры функций нескольких переменных:
а) объем параллелепипеда: V = abc, гдеa,b,c– его длина, ширина и высота;
б) сила гравитационного притяжения
между телами:
![]() ,
гдеm1 и m2
– массы тел,R–
расстояние между телами,- гравитационная постоянная.
,
гдеm1 и m2
– массы тел,R–
расстояние между телами,- гравитационная постоянная.
Это примеры функций трех переменных. Введем понятие функции nпеременных на примере пространства товаров.
Будем считать, что имеется n различных товаров. Количествоi– го товара обозначим xi(i = 1,2, . . . n).Тогданабор товаровобозначимX = (x1, x2, . . . , xn)– его можно рассматривать какn– мерный вектор. Множество всех наборов товаров{X}называетсяпространством товаров.ВекторыХназываются элементами этого пространства. Любые два набораX1 = (x11, x21, . . . , xn1)иX2 = (x12, x22, . . . , xn2)можно сложитьХ1 + Х2 по правилу сложения векторов и умножить любой набор товаров на любое неотрицательное число, последнее означает безграничную делимость товаров, т.е. товары «устроены» наподобие сахарного песка, а не автомобилей. Если в пространстве для всех его элементов определены операции сложения и умножения на число со всеми своими свойствами, то такое пространство называетсялинейным(Rn).Таким образом, пространство товаров является линейным.
Пусть каждый товар имеет цену pi (i = 1,2, . . . n, pi > 0).Тогда векторP = (p1,p2,, . . . ,pn) – называется вектором цен. Набор товаровХи вектор ценРимеют одинаковую размерность. Тогда их скалярное произведениеPX = p1x1 + p2x2 + . . . +pnxn есть число, которое называетсяценой набораили егостоимостьюи обозначаетсяС(Х). Если в линейном пространстве определена операция скалярного произведения, то такое пространство называетсяевклидовым(En).Пусть вектор цен известен, т.е. ценыp1,p2,, . . . ,pn – данные (фиксированные) величины, тогда стоимость набора товаров есть функцияnнеизвестных:С(Х) = p1x1 + p2x2 + . . . +pnxn.
Приведем примеры многомерных функций, используемых в экономике (их одномерные аналоги мы уже рассматривали).
Функция полезностиu(X) = u(x1, x2, . . . , xn)– субъективная числовая оценка данным индивидом полезности набора товаровХ = (x1, x2, . . . , xn).
Функция издержекC(Y) = C(y1, y2, . . . yn)– зависимость издержекСот объемов выпускаемой продукцииY = (y1, y2, . . . yn).
Производственная функция y = F(X) = F(x1, x2, . . . , xn) - зависимость объема выпускаемой продукцииyот объемов перерабатываемых ресурсовХ = (x1, x2, . . . , xn).Наиболее известная производственная функция –функция Кобба-Дугласа:
y = AKL1-, гдеA, -неотрицательные константы,K– объем вкладываемого в производство капитала,L –объем вкладываемых трудовых ресурсов.
Df. Если каждому вектору Х = (x1, x2, . . . , xn) из множества D по некоторому правилу (закону) f поставлено в соответствие одно и только одно число y E R, то говорят, что на множестве D задана (определена) функция n переменных: y = f(x1, x2, . . . , xn) или y = f(X).
При этом x1, x2, . . . , xn – независимые переменные (аргументы),y –зависимая переменная (функция).
Множество D – называетсяобластью определения функции; множество значений, принимаемых функциейE,называетсяобластью изменения функции.
§2. Свойства функций, заданных в евклидовом пространстве.
Многие понятия, определенные для функции одной переменной, почти без изменения переносятся на функции нескольких переменных, заданных в евклидовом пространстве. Так, функция одной переменной может быть четной, нечетной, возрастающей, убывающей, ограниченной и т.д. Как выглядят эти понятия для функции нескольких переменных?
Прежде чем дать определение возрастающей (убывающей) функции на множестве Еп, должно быть определеноотношение порядка:Х1 < Х2 понимается как строгое неравенство для всех компонент векторов:x11< x12, x21< x22, . . . , xn1< xn2.Тогда определение возрастающей (убывающей) функции нескольких переменных полностью аналогично соответствующему определению для функции одной переменной:
Df.Функцияy(X) называется возрастающей (убывающей) на множествеD Еп, еслиХ1, Х2 D, таких чтоХ1 < Х2 следует, чтоy(X1) < y(X2) (y(X1)>y(X2));функцияy(X) называется неубывающей (не возрастающей) на множествеD Еп, еслиХ1, Х2 D, таких чтоХ1 Х2 следует, чтоy(X1) y(X2) (y(X1) y(X2)).
Df.Функцияf(X), область определения которой(D(f))симметрична относительно нуля называется четной (нечетной), еслиf(-X) = f(X) (f(-X) = -f(X))для любогоX D(f).
Df.Функцияf(X)называется ограниченной сверху (снизу) на множествеD, если существует такоечисло m, чтоf(X) m (f(X) m) X D.
Df.Функцияf(X), ограниченная и сверху и снизу на множествеDназывается ограниченной на этом множестве, еслиm1 f(X) m2, X D(m1, m2 – некоторые числа).
Замечание.Из функции нескольких переменных можно получить несколько функций одной переменной: пусть функцияy = f(x1, x2, . . . , xn)– функцияnпеременных. Зафиксируем значения переменныхx2 = x20, x3 = x30, . . . , xn = xn0, ах1– пусть изменяется. Тогда получим функцию одной переменной: y1 = f(x1, x20, x30, . . . , xn0) = y1(x1).Аналогично можно получить функциюy2(x2), зафиксировав значения переменныхх1, х3, . . . ,хn, и т.п. Значит, выражение «функцияy = f(x1, x2, . . . , xn)возрастает пох1» означает, что возрастает функцияy1(x1)приx2 = x20, x3 = x30, . . . , xn = xn0.
Графическое изображение функции более чем двух переменных невозможно. В случае же если функция f– функция двух переменныхx иy, а значения ееz, тоz = f(x,y) и график этой функции – поверхность в пространствеR3, состоящая из точек(x,y,z), где(x,y) D(f) (D(f) – область определения функции).
Например.
z = x2 + y2 – параболоид.
О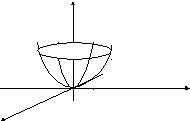 бласть
определенияD(z)– множество всех точек плоскостиOXY.
бласть
определенияD(z)– множество всех точек плоскостиOXY.
Область значений E(z): [0; +).Z
Y
О
X
2)
![]() - эллиптический конус.
- эллиптический конус.
Область определения D(z)– множество всех точек плоскостиOXY.
О бласть
значенийE(z):
(-; +).Z
бласть
значенийE(z):
(-; +).Z
O Y
X
3) x2 + y2 + z2 = R2– сфера с центром в точкеО(0;0;0)и радиусаR.
 Z
Z



 O
Y
O
Y

X
4 )
)![]() - эллипсоид с центром в точкеО(0;0;0).
- эллипсоид с центром в точкеО(0;0;0).
Z



 Y
Y
 O
O
O
O
X
Для образного представления функции многих переменных используются линии заданного уровня.
Df. Линией уровня функции двух переменных z = f(x,y) называется плоская кривая, получаемая при пересечении графика этой функции с плоскостью, параллельной плоскости OXY: z = C, где C = const.
Из определения следует, что линия уровня – это линия, в каждой точке которой значение функции не изменяется ( = С ).
Обычно линии уровня, соответствующие различным значениям С, проецируются на плоскостьOXY, тогда с их помощью можно исследовать характер поверхности, описываемой функциейz = f(x,y). Т.о. линии уровня функцииz = f(x,y)– это семейство кривых на координатной плоскостиOXY, описываемые уравнениями вида f(x,y)= С.