Файл: Ф_ЦИИ НЕСК_ ПЕРЕМ .doc

Аналогично вводится понятие поверхности уровнядля функцииnпеременных:

Пусть y = f(x₁, x₂, . . . , x_n)– функцияnпеременных иС– какое-либо число, тогда f(x₁, x₂, . . . , x_n)=С – уравнение поверхности уровняС.

В частности, если n= 3:u = f(x, y, z)– функция 3-х переменных, то уравнение поверхности этой функции уровняC:f(x, y, z)=С– это уравнение поверхности в 3-ех мерном пространстве

---

§3. Частные производные функции нескольких переменных.

Пусть функция y = f(x₁, x₂, . . . , x_n)(y = f(X))определена в некоторой окрестности точкиM(x₁, x₂, . . . , x_n) = M(X)и в этой точке функция имеет значениеf(M).

Дадим первому аргументу х₁приращениех₁, а другие переменные останутся неизменными. При этом получаем «новую» точкуМ₁(х₁+х₁, х₂, . . . , х_n), которая принадлежит указанной окрестности точкиМ, и значение функции в этой точкеf(M₁).

Тогда соответствующее приращение функции называется частным приращениемфункцииy = f(X)по переменнойх₁:

_х1y = f(M₁) – f(M) = f(х₁+х₁, х₂, . . . , х_n) - f(x₁, x₂, . . . , x_n) (1).

Аналогично можно определить частные приращения функции y = f(X)в точкеМ, соответствующие приращениюх_iлюбого изnаргументовx_i, i = 1,2,…n:

Пусть точка М_i(x₁, x₂, . . . , x_i+x_i, . . . , x_n) принадлежит указанной окрестности точкиМи значение функции в этой точкеf(M_i), тогда частное приращение этой функции по аргументуx_i:

_хiy = f(M_i) – f(M) = f(x₁, x₂, . . . , x_i+x_i, . . . , x_n) - f(x₁, x₂, . . . , x_n) (2).

Рассмотрим в данной точке M(x₁, x₂, . . . , x_n) = M(X)отношение частного приращения_хiyк соответствующему приращению i–ого аргумента -х_i:

(3).

---

Df.Если существуетпределотношения частного приращения функции_хiyв точкеМ к соответствующему приращению аргументах_iприх_i  0, то он называется частной производной функцииy = f(X)в точкеМ(Х)по аргументуx_iи обозначается:.

Таким образом, согласно определению:.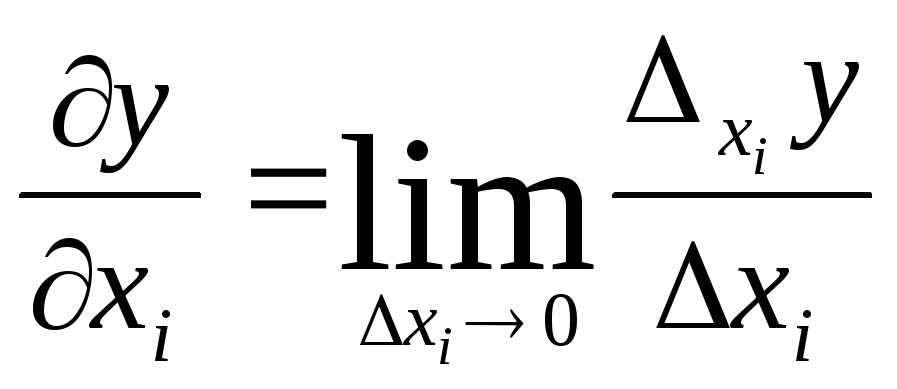

Частная производная функции y = f(X)по аргументуx_iв точкеМ₀(x₁⁰, x₂⁰, . . . , x_n⁰)обозначается:или.

Т.о., частная производная функции y = f(X)по аргументуx_iесть производная функции по этой переменной при условии, что остальные независимые переменные не изменяют своего значения, т.е.постоянны.Поэтому частные производные функцииy = f(X)находят по формулам и правилам вычисления производных функции одной переменной, при этом соответственно другие переменные считаютсяconst.

Примеры. Найти частные производные функций:

1. z = x² – 2xy + y²

________________________________ ________________________________

2. z = arctq(y/x)

________________________________________________________________________

3. u = ye^yz + ln(x² – 2y + z)

§3. Понятие дифференцируемости функции нескольких переменных.

Пусть функция y = f(X)определена в точкеM(X)и в некоторой ее окрестности. Составим полное приращение функции в точкеМ(Х)= M(x₁, x₂, . . . , x_n). Для этого дадим приращения каждой независимой переменнойМ(х₁, x₂, . . . , x_n). В результате получим «новую» точкуМ + М = (x₁+x₁, x₂+x₂, . . . , x_n+x_n), которая принадлежит данной окрестности точкиМ. Тогдаполным приращением y функцииy = f(X)в точкеM(X) будет являться разность:

---

y = f(M+M) – f(M) = f(x₁+x₁, x₂+x₂, . . . , x_n+x_n)-f(x₁, x₂, . . . , x_n)(1).

D

y =++. . .++₁x₁+₂x₂+ . . .+ _nx_n

f.Функцияy = f(X)называетсядифференцируемойв точкеM(X), если ее полное приращение(1)в этой точке можно представить в виде:

y =++. . .++₁x₁+₂x₂+ . . .+ _nx_n (2),

где ₁, ₂, . . . _n– бесконечно малые функции соответственно приx₁  0, x₂  0, . . . x_n  0.

Сумма первых nслагаемых в равенстве(2) представляет собойлинейноевыражение относительноx₁, x₂, . . . , x_n и являетсяглавной линейной частьюполного приращения функцииy = f(X), которое называетсяполным дифференциаломэтой функции и обозначаетсяdy или df(X):

dy = =++. . .+(3).

Для независимых переменных x₁, x₂, . . . , x_n полагаютx₁ = dx₁, x₂ = dx₂, . . . , x_n = dx_n,тогда формулу(3)можно переписать в виде:

dy = =++. . .+ (4).

---

Теорема 1. (необходимое условие дифференцируемости функции)

Если функция y = f(X)дифференцируема в точкеM(X), то она непрерывна в этой точке и имеет в ней частные производные ,i = 1,2,…n.

Теорема 2. (достаточное условие дифференцируемости функции)

Если функция y = f(X)имеет частные производные по всем аргументам в некоторой окрестности точкиМ(Х), причем эти производные непрерывны в самой точкеМ(Х), то данная функция дифференцируема в точкеМ(Х).(без доказательства).

---