Файл: Электронное пособие Scilab.pdf

81 

4. 

Содержание отчета 

1)  В форме комментариев: 

•  Название лабораторной работы 
•  ФИО студента, номер группы 
•  № варианта  

•  Индивидуальное задание 

2)  Протокол вычислений (сессии) в Командном окне, снабженный 

необходимыми комментариями. 
 

1.3.7. 

Контрольные вопросы по теме 

1)  Что такое файл-сценарий и каковы его особенности? 
2)  Каким образом файл-сценарий запускается на выполнение? 
3)  Что такое sci-функция? 
4)  В чем отличие файла-сценария от  sci-функции? 
5)  Может ли sci-функция иметь несколько выходных параметров? 
6)  Обращение к sci-функции. 
7)  Формат оператора input(). 
8)  Как с использованием оператора if…end реализовать стандартное, 

усеченное и вложенное разветвление? 

9)  Формат оператора множественного разветвления switch. 
10) Формат оператора регулярного цикла for…end, особенности задания 

значений переменной цикла. 

11) Назначение операторов continue и brek. 
12) Оператор итеративного цикла while…end и его структура. 

82 

Раздел 2. Технология решения  

вычислительных задач средствами Scilab 

Тема 2.1. Решение нелинейных уравнений 

2.1.1. Численное решение нелинейных уравнений 

2.1.2.  Лабораторная работа  
2.1.3.  Контрольные вопросы по теме 

2.1.1.  Численное решение нелинейных уравнений 

В общем виде уравнение можно представить, как f(x)=0. В зависимости 

от  вида  функции  f(x)различают  алгебраические  и  трансцендентные 
уравнения. 

Алгебраическими  уравнениями  называются  уравнения,  в  которых 

значение  функции  f(x)  представляет  собой  полином  n-й  степени  (n≥2). 
Всякое неалгебраическое уравнение называется трансцендентным. Функция 
f(x)в  таких  уравнениях  содержит  хотя  бы  одну  из  следующих  функций: 
показательную,  логарифмическую,  тригонометрическую  или  обратную 
тригонометрическую.  

Решением  уравнения  f(x)=0  называется  совокупность  корней ,  при 

которых  уравнение  обращается  в  тождество 

.  Однако,  точные 

значения  корней  могут  быть  найдены  аналитически  только  для  некоторых 
типов  уравнений.  Еще  меньше  возможностей  при  получении  точного 
решения  трансцендентных  уравнений.  Следует  отметить,  что  задача 
нахождения  точных  значений  корней  не  всегда  корректна.  Так,  если 
коэффициенты  уравнения  являются  приближенными  числами,  точность 
вычисленных  значений  корней  заведомо  не  может  превышать  точности 
исходных  данных.  Эти  обстоятельства  заставляют  рассматривать 
возможность  отыскания  корней  уравнения  с  ограниченной  точностью 
(приближенных корней). 

Задача  нахождения  корня  уравнения  с  заданной  точностью (

>0)считается  решенной,  если  найдено  приближенное  значение ,  которое 
отличается от точного значения корня   не более чем на значение : 

Для  отделения  корней  нелинейных  уравнений  применяются 

графический и аналитический методы.  Для уточнения корней с заданной 
степенью  точности  существуют  множество  численных  методов.  Самыми 
распространенными  из  них  являются:  метод  Ньютона,  метод  хорд,  метод 
итераций и метод половинного деления. 

x

f(x)

0



ε ε

x

ξ

|

ξ

x | ε.





83 

Процесс  нахождения  приближенного  корня  нелинейного  уравнения 

состоит из двух этапов:  

1)  отделение корня уравнения (локализация корня на отрезке); 
2)   уточнение корня с заданной точностью.  
Пример 2.1.1-1.Отделить и уточнить корень уравнения 

0

4

2



 x

x

. 

Согласно теореме о существовании и единственности корня на отрезке, 

найдем  отрезок,  на  концах  которого  функция 

x

x

f

x

4

2

)

(





имеет  разные 

знаки, а первая производная непрерывна и знакопостоянна (рис. 2.1.1-1). 

Рис. 2.1.1-1. Отделение корня нелинейного уравнения 

Условия  существования  и  единственности  корня  на  отрезке 

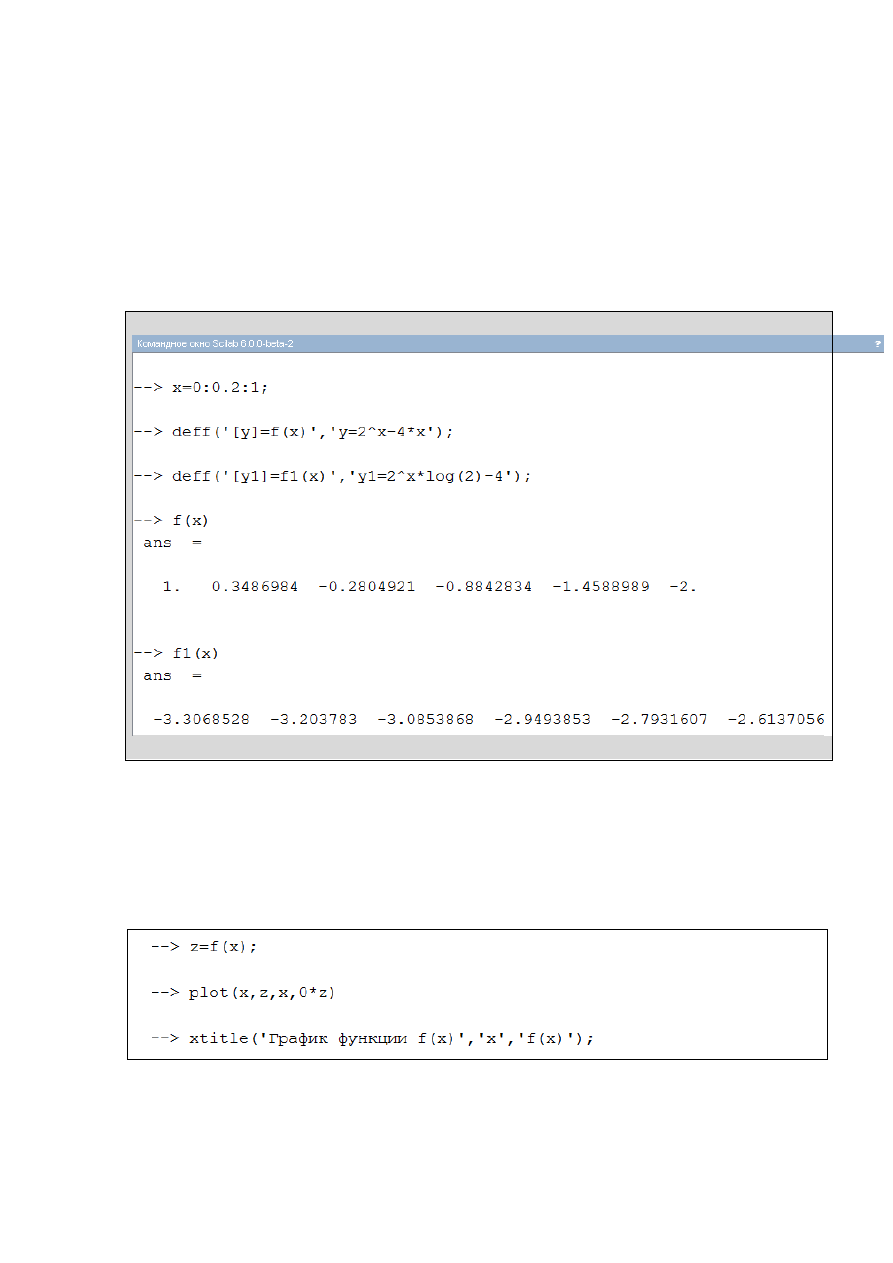
[0;1]выполняются.  Команды  построения  графика  функции  f(x)  на  отрезке 
[0;1]и график функции приведены на рис. 2.1.1-2. 

84 

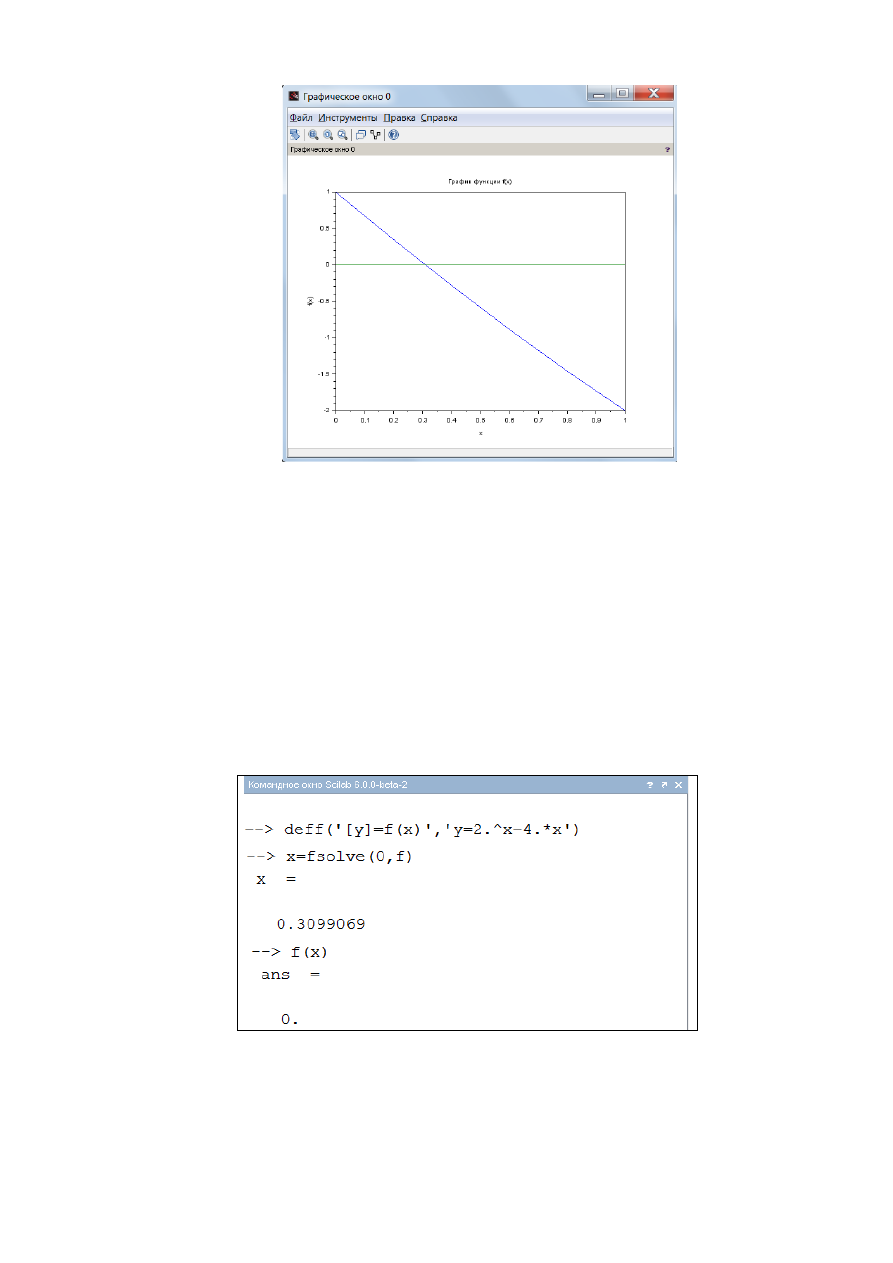
Рис. 2.1.1-2. Построение графика функцииf(x) 

Для  решения  нелинейных  уравнений  в  среде  Scilab  используются 

встроенные функции: fsolve() и roots(). 

Функция  fsolve()используется  для  нахождения  вещественных  корней 

уравнений вида f(х)=0. В простейшем варианте обращения кроме указателя на 
функцию,  корень  которой  необходимо  найти,  задается    х0,  с  которой 
начинается поиск:  

х = fsolve(x0,f), 
где f- функция, описывающая левую часть уравнения y(x)=0; 
x0- начальное приближение корня. 

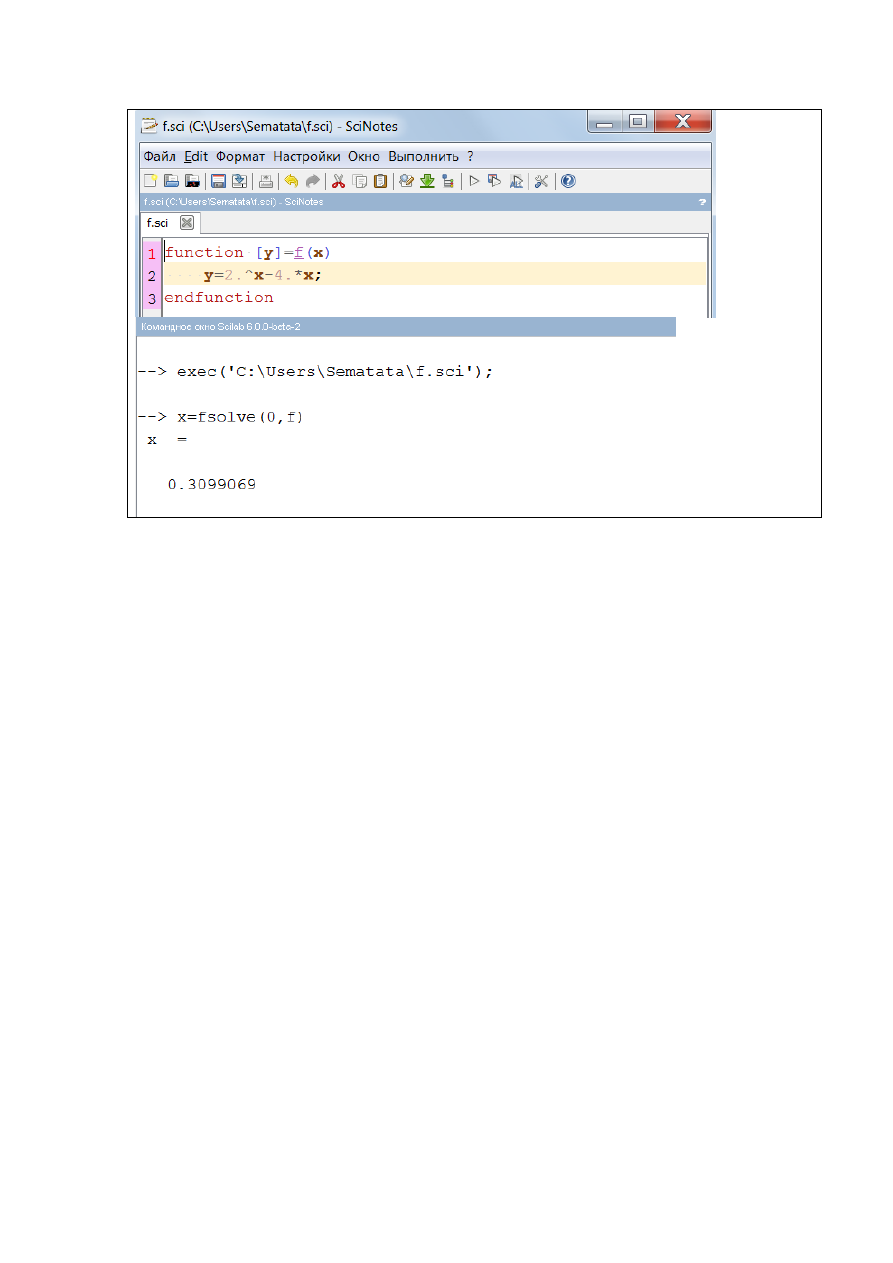
Рис. 2.1.1-3.  Уточнение корня уравнения с использованием функции fsolve() 

Вместо  явного  задания  выражения  для  функции  f(x)  можно  создать 

соответствующую функцию, запомнив ее в виде sci-файла (рис. 2.1.1-4).  

85 

Рис. 2.1.1-4.Описание  левой части уравненияв виде sci-файла 

Рассмотрим  технологию  определения  корня  с  помощью  функции 

solve() на следующем примере, в котором уравнение имеет несколько корней  
(рис.2.1.1-5). 

Пример 2.1.1-2

.

 Решить уравнение 

e

x

/5-2(x-1)

2

=0 . 

 
Отделим  корни  уравнения 

e

x

/5-2(x-1)

2

=0   

])

6

;

5

[

],

2

;

1

[

],

1

;

0

[

(

3

2

1







x

x

x

  и 

вычислим  все  корни,  последовательно  вызывая  функцию  fsolve()  с 
различными  начальными  приближениями.  Ниже  показана  возможность  
задания начальных приближений к корням в виде вектора, и тогда функцию 
можно вызвать один раз (рис. 2.1.1-5).