ВУЗ: Московский технический университет связи и информатики
Категория: Учебное пособие
Дисциплина: Информатика
Добавлен: 15.11.2018
Просмотров: 12840
Скачиваний: 228
91
z - матрица исходных данных (первая строка - массив х, вторая строка
–y);
a0 - вектор начальных коэффициентов (нулевой вектор из k элементов);
a – вектор коэффициентов, используемых в аппроксимирующей
функции) (a0, a1, …ak);
S - сумма квадратов отклонений измеренных значений от расчетных
данных.
Функция datafit(f,z,a0)возвращает вектор коэффициентов полинома
степени k, который с наименьшей среднеквадратичной погрешностью
аппроксимирует функцию, заданную таблично. Результатом является вектор
строка длиной k+1, содержащий коэффициенты полинома в порядке
увеличения степеней. Как правило, степень полинома много меньше
количества узлов(k<<n).
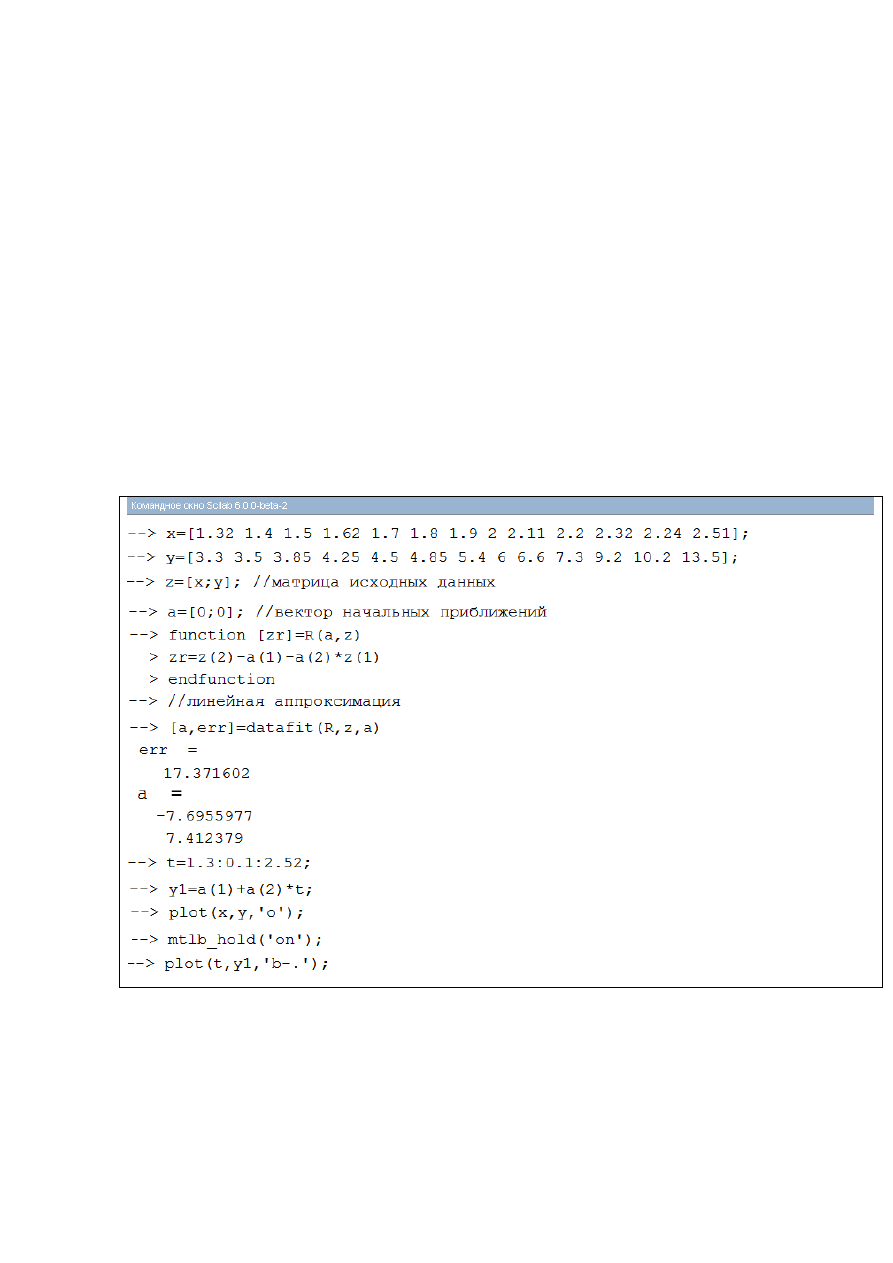
На рис.2.2.1-1 приведен пример линейной аппроксимации функции,
заданной таблицей. Функция R(a,z) рассчитывает разности между исходной и
аппроксимирующей функцией(y-(a
1
+a
2
x)=y-a
1
-a
2
x).
Рис. 2.2.1-1. Пример линейной аппроксимации функции
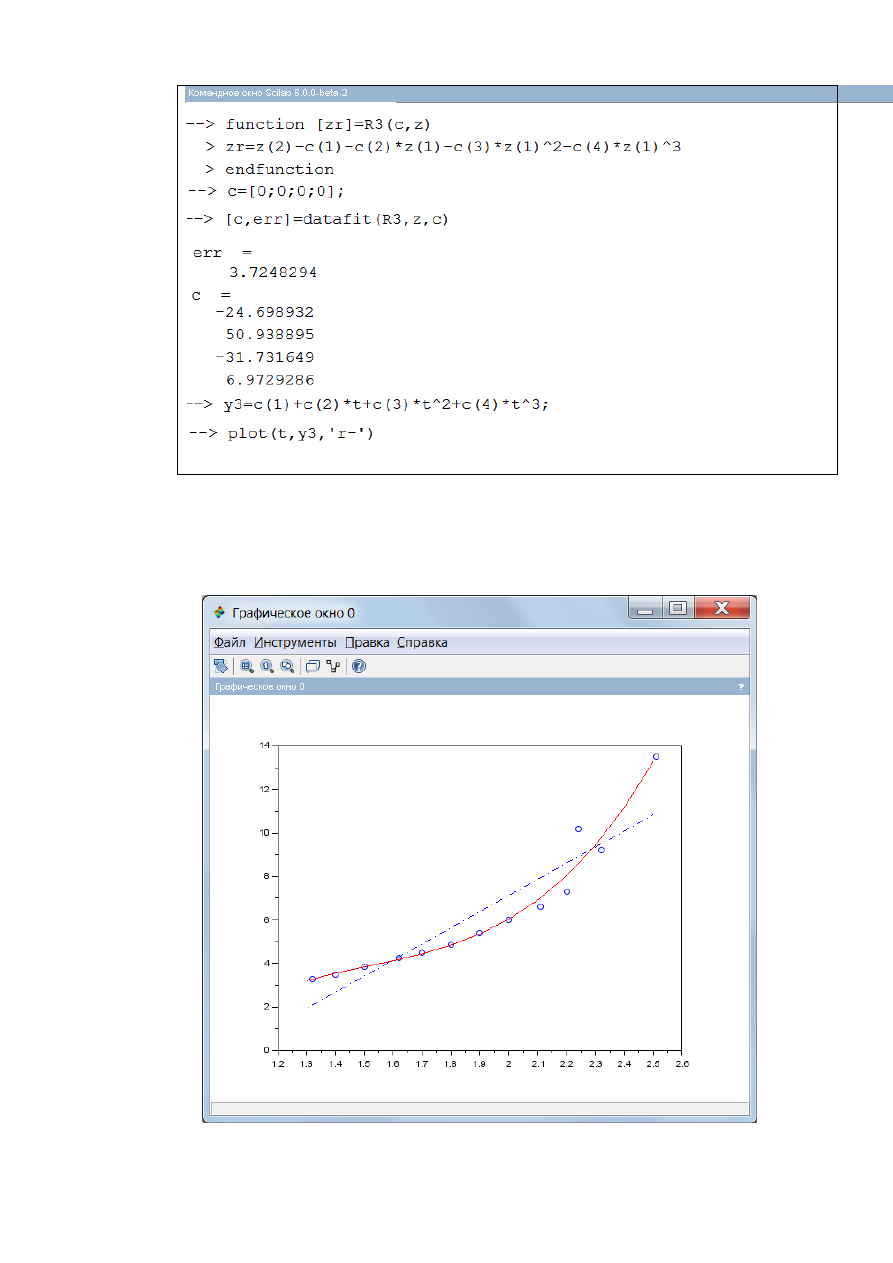
Добавим необходимые команды для кубической аппроксимации
(рис.2.2.1-2). Здесь разности между исходной и аппроксимирующей
функцией вычисляются функцией R3(с,z)
y-(с
1
+c
2
x+c
3
x
2
+c
4
x
3
)=y-c
1
-c
2
x-c
3
x
2
-c
4
x
3
.
92
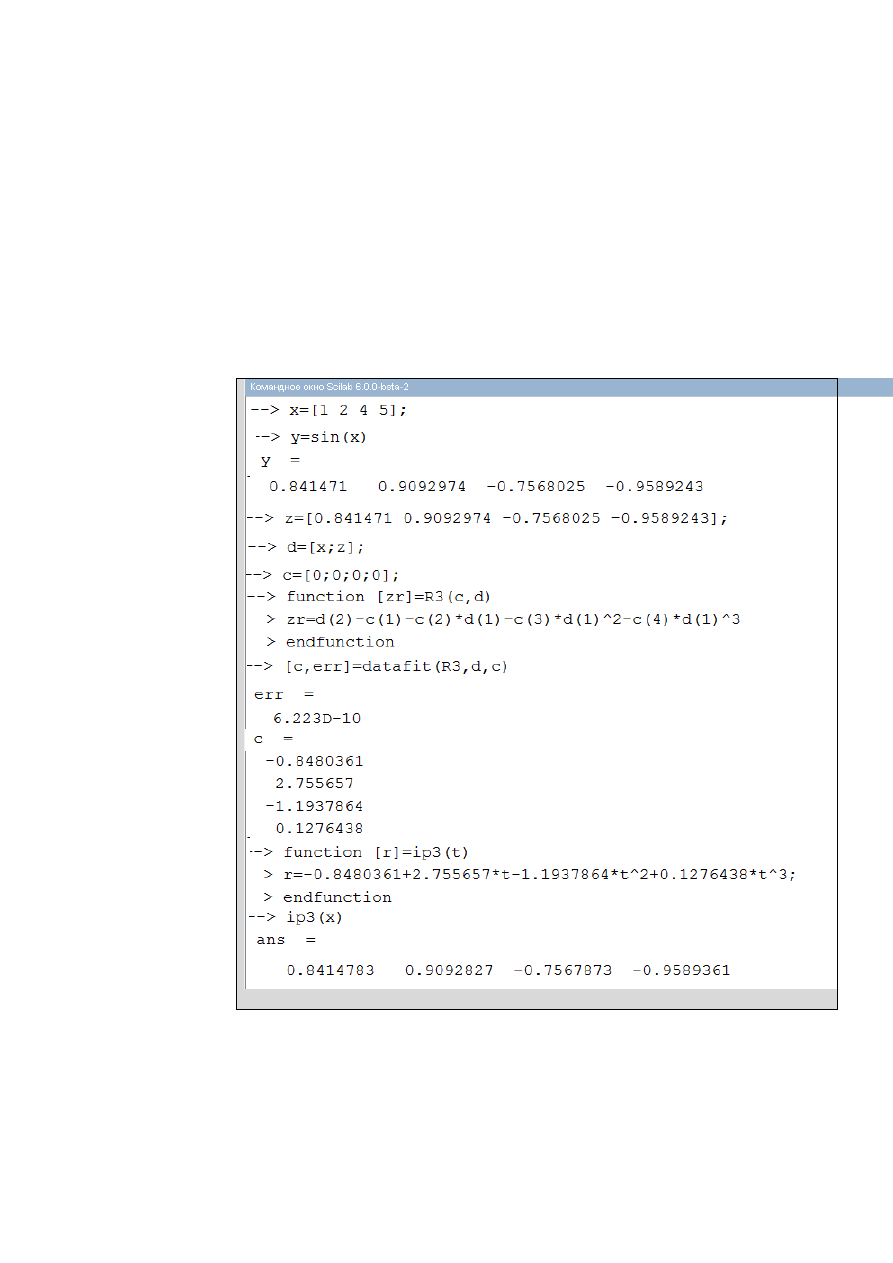
На рис.2.2.1-3 приведены графики исходной и аппроксимирующих
функций.
Рис. 2.2.1-3. Графики исходной и аппроксимирующих функций
93
Чтобы использовать функцию datafit() для решения задачи
интерполяции необходимо, чтобы степень этого полинома была на единицу
меньше количества узловых точек.
Пример 2.2.1-1. Используя в качестве узлов интерполяции
x=1,2,4,5, построить полином, интерполирующий функцию
)
(
)
(
x
Sin
x
y
.
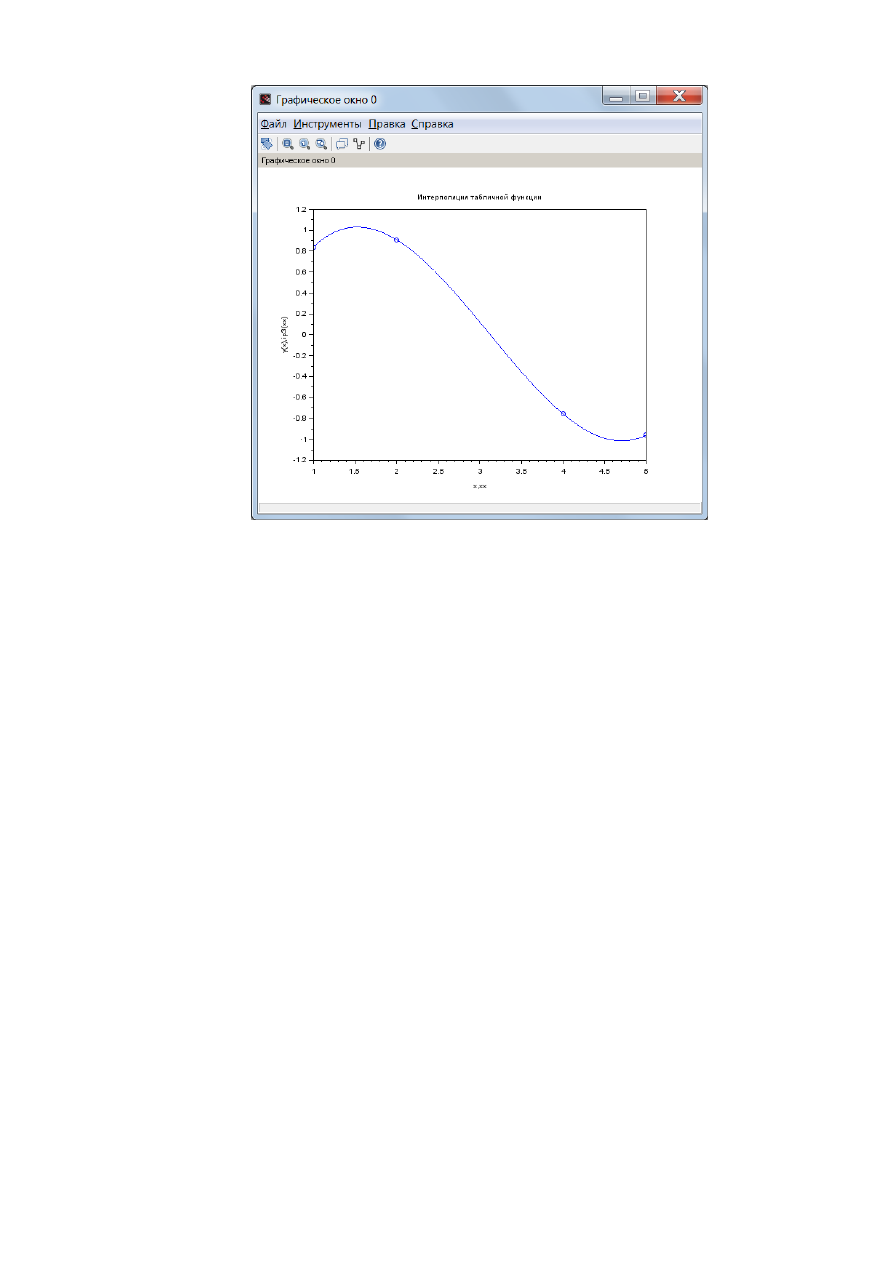
В начале, получим таблицу значений функции и проведем ее
интерполяцию ее с использованием функции datafit() (рис. 2.2.1-5). Графики
интерполяционных узлов и интерполяционного полинома приведены на рис.
2.2.1-6.
Рис. 2.2.1-5. Интерполяция таблично заданной функции
с использованием функции Scilab datafit()
94
Рис. 2.2.1-6. Графики интерполируемой и интерполирующей функций
При большом количестве базовых точек интерполяции полиномом
может оказаться малопродуктивной, поэтому нередко используют
интерполяцию сплайнами. Идея сплайн-интерполяции состоит в разбиении
диапазона интерполирования на отрезки, в пределах которых используются
разные функции одного вида (чаще всего алгебраические многочлены). Эта
функция и ее несколько производных на всем диапазоне интерполяции
непрерывны. В результате имеем кусочно-гладкую интерполяционную
зависимость.
Один из наиболее распространенных вариантов интерполяции
интерполяция кубическими сплайнами . Кроме того существуют
квадратичные и линейные сплайны.
В Scilab для построения линейной интерполяции служит функция
y=interpln(z,x),
где z - матрица исходных данных;
x - вектор абсцисс;
y - вектор значений линейного сплайна в точка x.
Рассмотрим пример использования функции interpln().

95
Пример 2.2.1-2
.
Используя значения интерполирующей функции,
заданной
таблично,
и
выполнить
сплайн-интерполяцию
с
использованием линейных сплайнов и получить значения функции в
точке х=0.58.
x
-1 0 1 2
y(x)
4 2 0
1
Рис. 2.2.1-7. Вычисление функции в точке х=0.58
Построение кубического сплайна в Scilab состоит из двух этапов:
вначале вычисляются коэффициенты сплайна с помощью функции
d=splin(x,y), а затем рассчитывается значения интерполяционного полинома
в точке y=interp(t,x,y,d).
Функция d=splin(x,y) имеет следующие параметры:
x - строго возрастающий вектор, состоящий минимум из двух
компонент;
y- вектор того же формата, что и x;
d - результат работы функции, т.е. коэффициенты кубического сплайна.
Для функции y=interp(t,x,y,k) параметры x, y и d имеют те же
значения, параметр t - это вектор абсцисс, а y - вектор ординат, являющихся
значениями кубического сплайна в точках x.
Пример 2.2.1-3
.
Найти приближенное значение функции при
заданном значении аргумента с помощью интерполяции кубическими
сплайнами в точках x1 = 0,702, x2 = 0,512, x3 = 0,608.
x
0.43
0.48
0.56
0.62
0.7
0.75
y(x)
1.635
1.732
1.876
2.033
2.228
2.359