ВУЗ: Московский технический университет связи и информатики
Категория: Учебное пособие
Дисциплина: Информатика
Добавлен: 15.11.2018
Просмотров: 12842
Скачиваний: 228
86
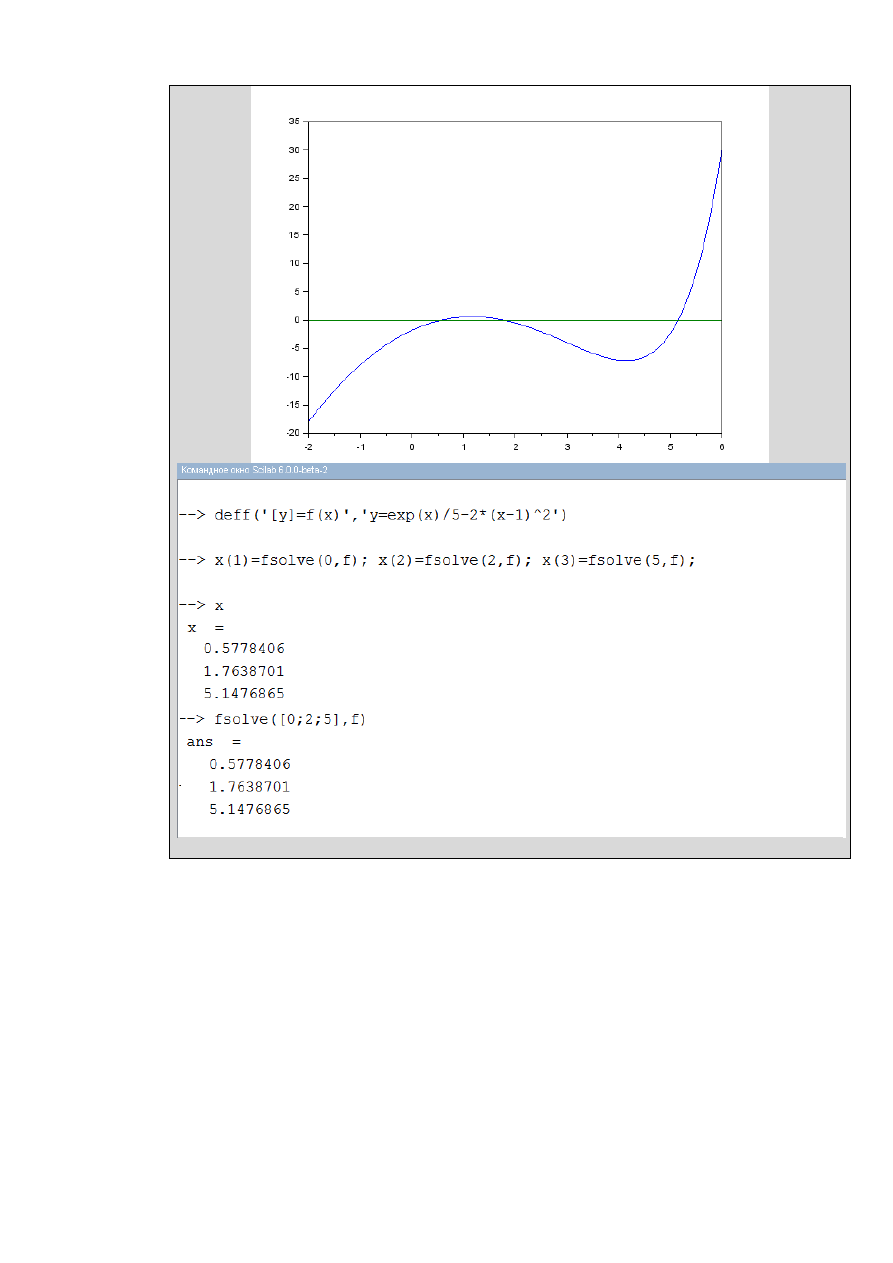
Рис. 2.1.1-5. Уточнение нескольких корней уравнения с использованием
функции solve()
Функция Scilab roots() используется для вычисления корней полинома
вида
1
1
2
1
...
)
(
n
n
n
n
a
x
a
x
a
x
a
x
P
. Перед ее использованием создается
список коэффициентов (даже нулевых), затем выполняется функция
poly(a, ‘x’, [‘fl’]),
где a- это число или матрица чисел, x - символьная переменная, fl –
необязательная символьная переменная, определяющая способ задания
полинома. Символьная переменная fl может принимать только два значения
"roots" или "coeff” (соответственно ‘r’или ‘c’). Если fl=c, то будет
87
сформирован полином с коэффициентами, хранящимися в параметре a. Если
же fl=r, то значения параметра a воспринимаются функцией как корни, для
которых
необходимо
рассчитать
коэффициенты
соответствующего
полинома. По умолчанию fl=r.
Теперь можно использовать функцию roots(p), у которой в качестве
аргумента указывается имя полинома, созданного функцией poly
(рис. 2.1.1-6).
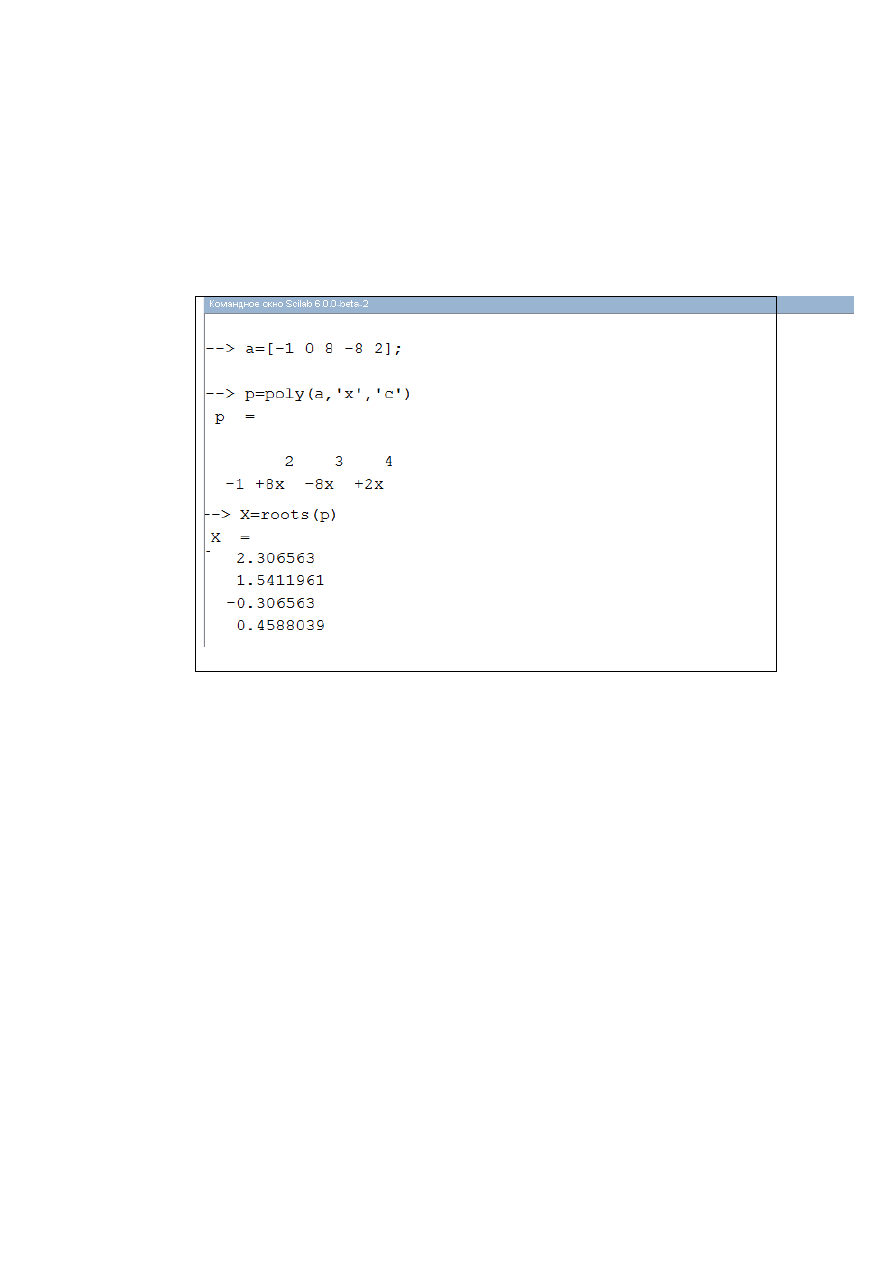
Рис. 2.1.1-6. Уточнение корня уравнения с использованием функции roots()
Вычисление корней полинома
16
10
16
10
)
(
2
4
5
6
6
x
x
x
x
x
x
P
с
использованием команды roots(а) показало, что у полинома есть четыре
действительных корня.

88
2.1.2. Лабораторная работа по теме
«Технология решения нелинейных уравнений
средствами пакета Scilab»
1. Вопросы, подлежащие изучению
1) Задание функций и их производных с использованием средств пакета
Scilab.
2) Получение таблиц значений функций в заданных границах изменения
аргумента.
3) Построение графиков функций средствами Scilab.
4) Этапы решение нелинейных уравнений: отделение и уточнение корня.
5) Решение нелинейных уравнений с использованием встроенных
функций пакета Scilab: fsolve(), poly() и roots().
2. Общее задание
1) Изучите материал Темы 2.1 (п. 2.1.1).
2) Выберите индивидуальный вариант задания из табл. 2.1.2-1.
3) Отделите корень нелинейного уравненияf(x)=0с использованием
средств пакета Scilab, для чего:
• Построить графики функции f(x)и ее первой производной;
• на выбранном отрезке пересечения графика с осью ОХ получить
таблицы значений функции f(x)и ее первой производной
• проверить условие существования единственного корня на
выбранном отрезке.
4) Решите нелинейное уравнение с использованием функций fsolve() .
5) Предъявите результаты выполнение задания на ПК преподавателю.
3.
Варианты индивидуальных заданий
Таблица 2.1.2-1
№
Уравнение
№
Уравнение
1
????
2
− 6 ln(???? + 1) + 2,8 = 0
16
2????
2
− sin ???? − 1,5 = 0
2
????
2
− 4 sin ???? + 0,8=0
17
2 cos(???? − ????
3
) − ???? = 0
3
????
2
− 3 sin ???? − 2,4
18
????
2
− 3,4 ln(1 + ????) − 1 = 0
4
????
2
+ sin ???? − 0,5√(1 + 2????)
3
=0
19
????
????
− (???? + 1)
2
− 2 = 0
5
3????
2
− 2 cos(???? + 1) − 4,8 = 0
20
????
2
− sin ???? = 0
6
????
2
− 1,5 cos(???? + 3) − 1,8 = 0
21
????
????
− 4???? − 9,5 = 0

89
7
ln(???? + 2) + cos(2 + ????) − 0,35
= 0
22
????
2
− 3sin ???? − 2???? = 0
8
????
3
− 4,8 sin(1 + 2????) − 1=0
23
3 − 2 sin ???? − √????
2
+ 1 = 0
9
????
2
− 2 sin(???? + 1) − 2 = 0
24
−(2 + 3 sin ???? − √????
2
+ 2 = 0
10
????
????−3
− ln(???? + 3) + 1 = 0
25
????
−0,4????
+ 3????
2
− 5???? − 3 = 0
11 − sin ???? − √???? + 1 = 0
26
????
2
+ cos(???? − 4) + √???? + 1 −
3=0
12
cos(???? − 0,2????
2
) − ???? + 6 = 0
27
????
2
− ln ???? − 3 = 0
13
????
????
− 4???? = 0
28
−???? + ????
0,5????
= 0
14
0,1????
2
+ ???? ln ???? − ???? + 0,5 = 0
29
− sin ???? − √1 + ???? + 2 = 0
15
2????
−????
+ ????
????
− 4=0
30
4????
3
+ 2????
4
+ 9,5????
−2????
− 35
= 0
4.
Содержание отчета
1) В форме комментариев:
• Название лабораторной работы
• ФИО студента, номер группы
• № варианта
• Индивидуальное задание
3) Протокол вычислений (сессии) в окне Командного окна, снабженный
необходимыми комментариями.
2.1.3.
Контрольные вопросы по теме
1) Что называется, нелинейным уравнением?
2) Этапы решения нелинейного уравнения.
3) Графическое отделение корней нелинейного уравнения средствами
Scilab.
4) Аналитическое отделение корней нелинейного уравнения средствами
Scilab.
5) Способы задания функции нелинейного уравнения.
6) Назначение и формат функции poly().
7) Назначение и формат функции fsolve().
8) Назначение и формат функции roots().

90
Тема 2.2. Технология аппроксимации
интерполяции функций в среде пакета MatLab
2.2.1. Аппроксимация и интерполяция функций
2.2.2. Лабораторная работа
2.2.3. Контрольные вопросы по теме
2.2.1. Аппроксимация и интерполяция функций
Пусть имеется набор узловых точек x
k
(где k=1,2,…,n) и значения
функции y(x
k
)в этих точках, а также некоторая функция f(x,a
1
, a
2
, …,a
m
),
которая кроме аргумента х зависит еще и от параметров a
s
(где s=1, 2, …m).
Задача аппроксимации состоит в том, чтобы подобрать такие значения
параметров a
s
, что функция f(x, a
1
, a
2
, …a
m
)наилучшим образом описывала
бы исходную функцию. Как правило, m<<n, поэтому добиться, чтобы
функция f(x, a
1
, a
2
, …a
m
) давала точные результаты даже в узловых точках не
удастся. Нужен критерий, который оценивает точность аппроксимации
таблично заданной функции. Например, в методе наименьших квадратов в
качестве такого критерия используется среднеквадратическое отклонение
1
))
(
(
0
2
m
x
f
y
m
i
i
i
Частным
случаем
задачи
аппроксимации
является
задача
интерполяции функции. В этом случае также имеем набор узловых точек x
k
(где k=1,2,…,n) и значения функции y
k
в этих точках. Однако, в
соответствии с критерием интерполяции, требуется построить такую
функцию f(x), которая в узловых точках x
1
, x
2
,…,x
n
принимала бы значения
y
1
, y
2
, …,y
n
, то есть f(x
k
) = y
k
для всех kот 1 доn.Чаще всего функцию f(x)
ищут в виде полинома, степень которого n-1. Поэтому задача сводится к
определению коэффициентов интерполяционного полинома на основании
значений функции в базовых точках.
На практике для решения задачи интерполяции (вычисления значений
функции в точках, несовпадающих с узлами интерполяции) используются
интерполяционные формулы Ньютона и формула Лагранжа.
Для выполнения полиномиальной аппроксимации в Scilab используется
функция
[a,S]=datafit(f,z,a0),
где f - функция, с помощью которой можно вычислить разницу между
заданными и расчетными значениями (y-f(x,a
0
, a
1
, …a
k
);