ВУЗ: Московский технический университет связи и информатики
Категория: Учебное пособие
Дисциплина: Информатика
Добавлен: 15.11.2018
Просмотров: 12837
Скачиваний: 228
96
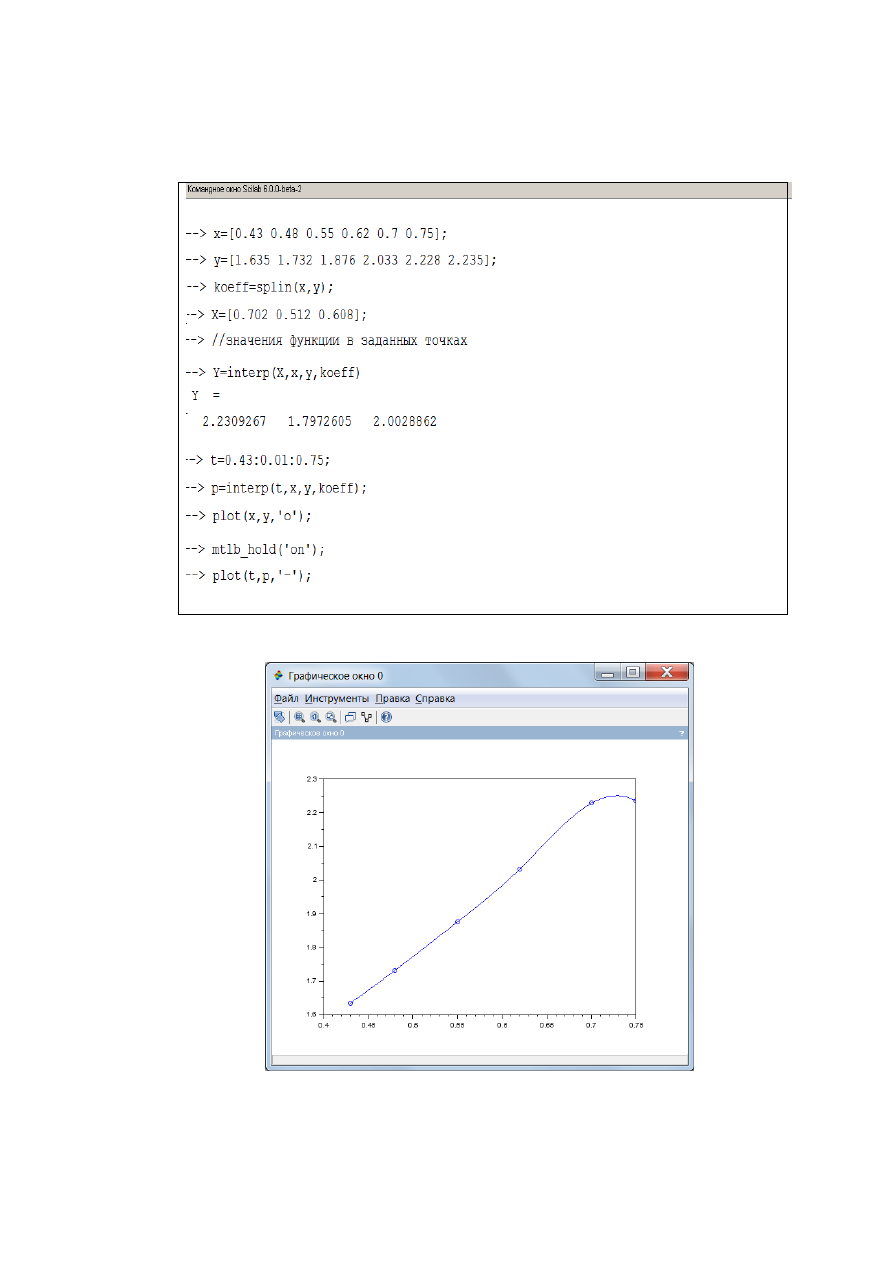
На рис.2.2.1-8 и рис.2.2.1-9 приведены команды, необходимые для
проведения интерполяции таблично заданной функции и построение
графиков интерполируемой функции и интерполирующих ее
с
использованием кубических сплайнов.
Рис. 2.2.2-8. Команды построения графиков интерполяционных функций
Рис. 2.2.2-9. График функции, полученной с использованием
кубических сплайнов

97
2.2.2
. Лабораторная работа по теме
«Технология аппроксимации и интерполяции
функций»
1.
Вопросы, подлежащие изучению
1) Задание векторов и матриц в пакете Scilab.
2) Технология
аппроксимации функции, заданной таблично, с
использованием функций datafit().
3) Технология линейной, кубической и сплайн-интерполяции таблично
заданной функции с использованием функций interpln().
4) Получение интерполяционных многочленов в явном виде.
5) Построение графиков аппроксимирующих и интерполирующих
функций.
2.
Общее задание
1) Изучите материал Темы 2.2. (п. 2.2.1).
2) Выберите
индивидуальное задание: номера узлов и номер
аппроксимируемой функции из табл. 2.2.2-1; узлы аппроксимации и
значения функции в узлах из табл. 2.2.2-2.
3) Задайте в виде векторов значения узлов и значения функции в
выбранных узлах;
4) Вычислите
коэффициенты аппроксимирующих функции для
линейной, квадратичной и кубической аппроксимации с использованием
функции datafit( )и получите три аппроксимирующие функции в явном
виде.
5) Получите
с
использованием
этих
функций
значение
аппроксимирующей функции в произвольной точке, принадлежащей
отрезку, но не совпадающей с узлами аппроксимации, и сравните
полученные результаты.
6) Построите графики табличной и трех аппроксимирующих функций в
одном шаблоне, снабдив их легендой.
7) Проведите линейную и кубическую интерполяцию функции с
использованием функции interpln(), заданной таблично. Получив
значения интерполирующей функций в точке, не совпадающей с узлами
интерполяции и сравните полученные результаты.
8) Построите графики табличной и двух интерполирующих функций в
одном шаблоне, снабдив их легендой.
9) Предоставьте результаты работы преподавателю, ответить на
поставленные вопросы.
98
10) Выполните команду clear all.
11) Оформите отчет по выполненной работе.
3.
Варианты заданий
Таблица 2.2.2-1
Вариант №
Номера узлов x
i
Номер функции
1
1 3 5 7 9 10 13
)
(
1 x
f
2
1 2 4 5 7 10 12
)
(
1 x
f
3
1 3 6 7 10 11 13
)
(
1 x
f
4
1 2 4 7 9 11 13
)
(
1 x
f
5
3 6 7 9 10 11 12
)
(
1 x
f
6
2 3 6 8 9 10 13
)
(
1 x
f
7
1 4 5 7 9 11 12
)
(
1 x
f
8
1 2 4 7 9 12 13
)
(
1 x
f
9
2 3 5 7 8 11 12
)
(
1 x
f
10
1 3 6 7 9 10 13
)
(
1 x
f
11
1 3 7 8 10 11 13
)
(
2 x
f
12
1 2 5 6 7 10 12
)
(
2 x
f
13
1 4 5 8 10 12 13
)
(
2 x
f
14
1 3 5 7 9 10 13
)
(
2 x
f
15
1 3 6 7 8 10 13
)
(
2 x
f
16
1 4 5 7 9 11 12
)
(
2 x
f
17
2 4 5 6 8 12 13
)
(
2 x
f
18
1 4 5 7 9 11 12
)
(
2 x
f
19
1 4 5 8 10 11 12
)
(
2 x
f
20
2 4 5 6 8 12 13
)
(
2 x
f
21
1 4 5 810 12 13
)
(
3 x
f
22
2 3 6 8 9 10 13
)
(
3 x
f
23
1 3 5 8 10 12 13
)
(
3 x
f
24
1 4 5 7 9 11 12
)
(
3 x
f
25
2 4 5 6 8 12 13
)
(
3 x
f
26
3 4 5 7 8 9 12
)
(
3 x
f
27
3 5 8 10 11 12 13
)
(
3 x
f
28
2 4 7 9 10 11 13
)
(
3 x
f
29
2 4 5 7 8 10 12
)
(
3 x
f
30
1 4 5 7 9 11 13
)
(
3 x
f
99
Таблица 2.2.2-2
i
x
i
)
(
1
i
x
f
)
(
2
i
x
f
)
(
3
i
x
f
1
-5
1.38
2.44
1.676
2
-4.5
1.221
2.359
2.025
3
-4
1.511
1.751
1.736
4
-3.5
1.501
2.13
1.203
5
-3
1
1.455
1.511
6
-2.5
0.728
1.482
1.362
7
-2
0.976
1.437
0.75
8
-1.5
1.065
0.803
0.976
9
-1
0.599
1.175
0.957
10
-0.5
0.192
0.49
0.272
11
0
0.3
0.375
0.3
12
0.5
0.319
-6.51*10
-3
0.165
13
1
-0.405
-1.965
-1.185
4.
Содержание отчета
1) В форме комментариев:
• Название лабораторной работы
• ФИО студента, номер группы
• № варианта
• Индивидуальное задание
2) Протокол вычислений (сессии) в Командном окне, снабженный
необходимыми комментариями.
2.2.3. Контрольные вопросы по теме
1) Что такое аппроксимация функции, и в каких случаях она
используется?
2) В чем отличие аппроксимации от интерполяции?
3) Какой метод аппроксимации реализован в функции datafit()?
4) Что служит результатом выполнения функции datafit()?
5) Назначение и формат функции interpln()?
6) Каким параметром определяется тип интерполяции в функции
interpln()?

100
Тема 2.3. Технология интегрирования
в среде Scilab
2.3.1.Вычисление неопределенных и определенных интегралов
2.3.2. Лабораторная работа
2.3.3. Контрольные вопросы по теме
2.3.1. Вычисление неопределенных и
определенных интегралов
При вычислении определенных интегралов первообразную функцию
F(x)не всегда удается выразить аналитически, а кроме того иногда
подынтегральная функция f(x) задана в виде таблицы (x
i
и y
i
, где i= 1, 2, …,
n).Это приводит к необходимости использования численных методов
интегрирования.
Существует ряд методов численного интегрирования. Во всех этих
методах вычисление осуществляется по приближенным формулам,
называемым квадратурами.
Суть получения формул численного интегрирования состоит в том, что
на элементарных отрезках интегрирования подынтегральную функцию
заменяют простейшим интерполяционным полиномом, который легко может
быть проинтегрирован в аналитическом виде. Так, например, для получения
формул прямоугольников, трапеций и Симпсона используют полиномы
соответственно нулевой, первой и второй степени.
Формулы прямоугольников:
,
)
(
1
1
0
n
i
k
n
i
i
b
a
y
h
y
h
dx
x
f
где:h–шаг интегрирования;
y
i
– значение подынтегральной функции от аргумента x
i
, k=0, 1, …,n;
n–число разбиений интервала интегрирования a, b.
Формула трапеций:
,
2
2
)
(
1
1
0
n
n
i
i
b
a
y
y
y
h
dx
x
f
где:h– шаг интегрирования;
y
0
– значение подынтегральной функции при х = a;
y
n
– значение подынтегральной функции при х = b;
Формула Симпсона:
,
4
2
...
2
4
3
)
(
1
2
2
1
0
n
n
n
b
a
y
y
y
y
y
y
h
dx
x
f