ВУЗ: Московский технический университет связи и информатики
Категория: Учебное пособие
Дисциплина: Информатика
Добавлен: 15.11.2018
Просмотров: 12836
Скачиваний: 228
101
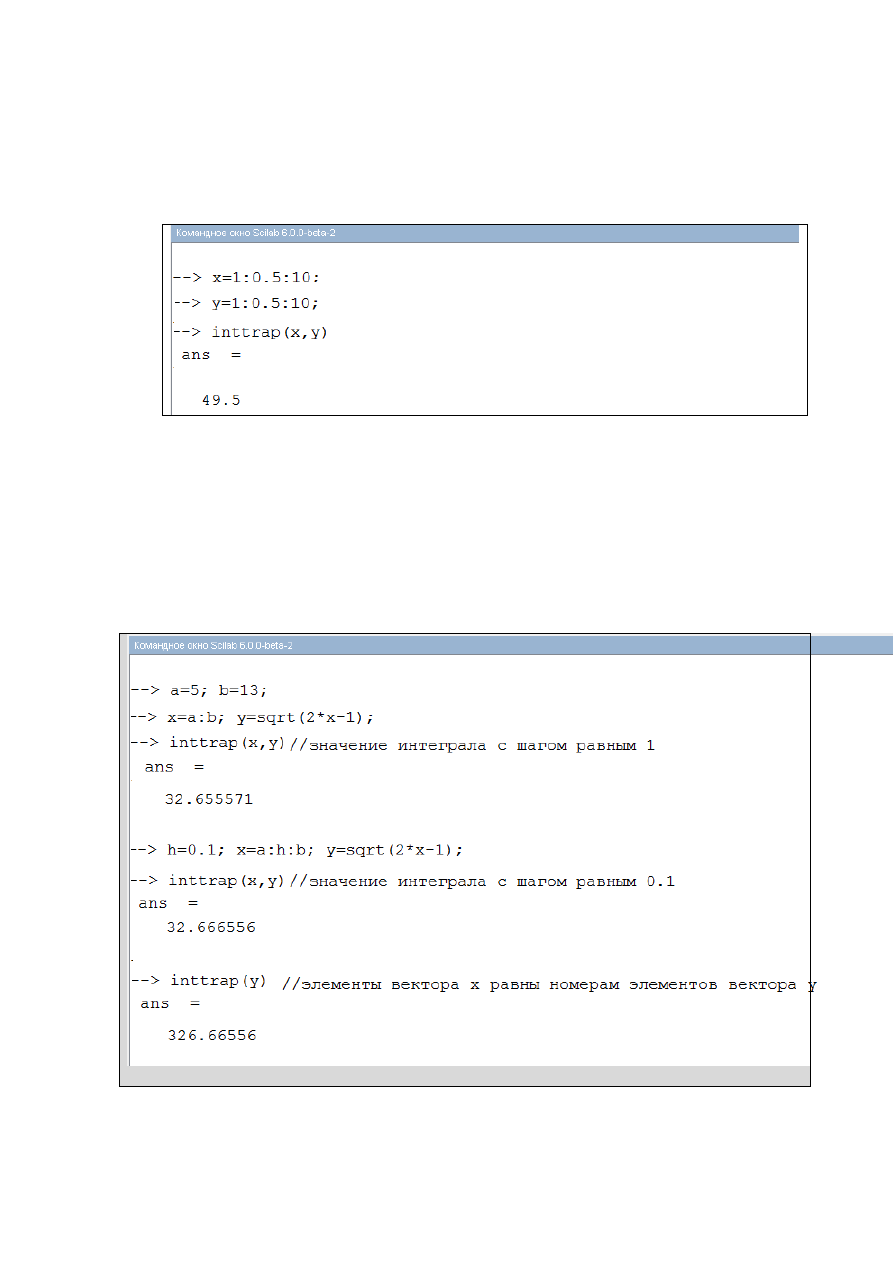
Для вычисления интеграла
b
a
x
x
y )
(
по формуле трапеции в Scilab
используется функция inttrap([x],y). Эта функция вычисляет площадь
фигуры под графиком функции y(x), которая описана набором точек
(x, y). Простейший пример использования функции inttrap() приведен на
рис.2.3.1-1.
Рис.2.3.1-1. Вычисление интеграла по формуле трапеций
Параметр х является необязательным. Для формата функции inttrap(y)
элементы вектора х могут принимать значения номеров вектораy.
Рассмотрим несколько примеров вычисления значений определенных
интегралов методом трапеций (рис. 2.3.1-2). В последнем примере
использован формат inttrap(y), то есть значения х заменены номерами
элементов вектора y. В результате получено другое значение интеграла. Это
показывает, что получена площадь совершенно другой фигуры.
Рис.2.3.1-2. Примеры вычисления определенных интегралов с
использованием функции inttrap()
102
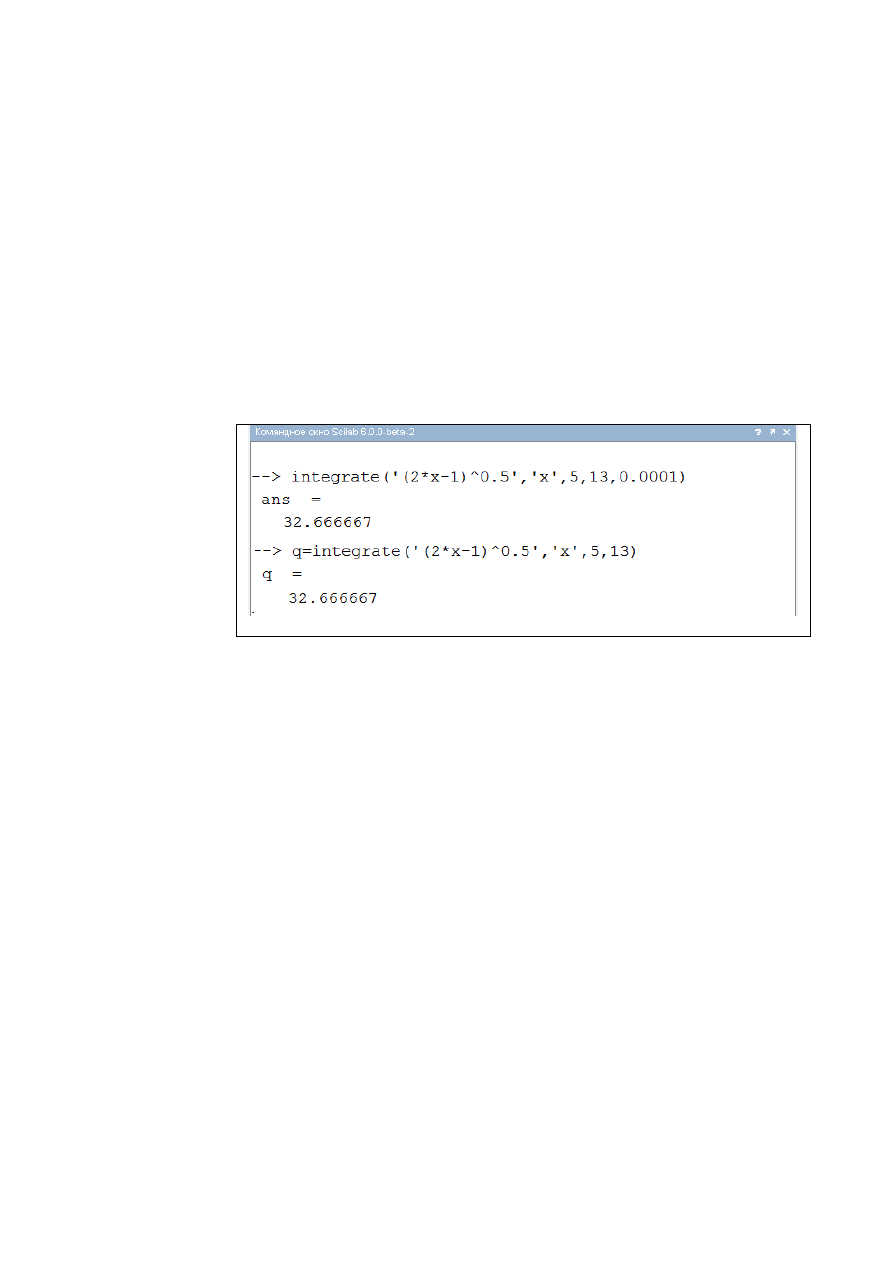
Для вычисления интеграла по формуле Симпсона в Scilab
применяется функция integrate() имеющей формат
integrate(fun, x, a, b, [,er1 [,er2]])
где fun- функция, задающая подынтегральное выражение в символьном виде;
x- переменная интегрирования, так же задается в виде символа;
a, b- пределы интегрирования, действительные числа;
er1 и er2– переменные, задающие абсолютную или относительную точность
вычислений (действительные числа).
При обращении к этой функции шаг интегрирования не задается, а
используется параметр – требуемая точность вычисления интеграла
(рис.2.3.1-3). Если погрешность вычисления интеграла отсутствует, то
вычисление проводится с погрешностью, установленной по умолчанию.
.
Рис.2.3.1-3. Вычисление определенных интегралов
с использованием функции integrate()

103
2.3.2. Лабораторная работа по теме
«Технология интегрирования в среде scilab»
1. Вопросы, подлежащие изучению
1) Вычисление значения определенного интеграла с использованием
функций.
2) Вычисление значения определенного интеграла с использованием
функций Scilab inttrap() и integrate().
3) Формулы численного интегрирования: средних прямоугольников,
трапеций и Симпсона.
2. Общее задание
1) Изучите материал Темы 2.3 (п. 2.3.1.).
2) Выберите из табл. 2.3.2-1 вариант индивидуального задания.
3) Вычислите определенный интеграл с использованием функцииScilab,
реализующей формулу трапеций, - inttrap(x, y), предварительно
получив таблицу значений подынтегральной функции с шагом h, и
задав значения аргумента и функции в виде векторов.
4) Вычислите значение определенного интеграла с использованием
функции Scilab, реализующей формулу Симпсона, – integrate ('f',a,b),
где f– имя функции, взятое в одинарные кавычки.
5) Предоставьте результаты работы преподавателю, ответьте на
поставленные вопросы.
6) Выполните команду clear all.
7) Оформите отчет по выполненной работе.
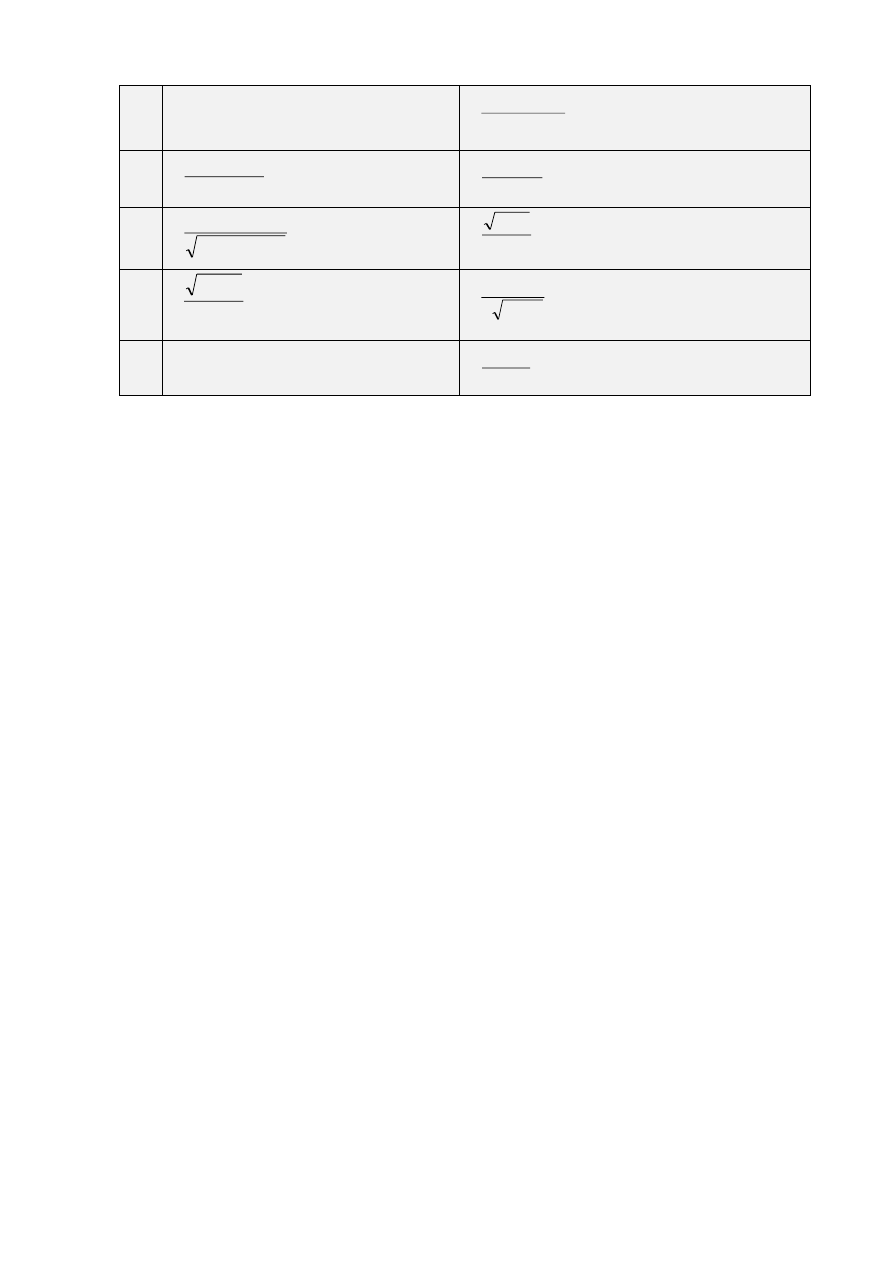
1. Варианты индивидуальных заданий
Таблица 2.3.2-1
№
Интеграл 1
Интеграл 2
1
dx
e
x
Cos
x
)
)
(
4
0
)
2
(
8
dx
x
Sin
e
x
2
x
x
x
4
1
3
1
2
/
1
)
1
)(
5
/
(
x
x
x
x
Cos
3
x
x
x
)
1
(
1
2
5
5
.
3
2
/
)
ln(
5
x
x
x
4
x
x
2
2
1
5
,
1
5
.
0
2
2
)
ln(
x
x
x
5
x
e
x
Sin
x
)
)
(
8
(
5
.
2
5
.
1
)
ln(
/
)
4
(
1
x
x
x
Sin

104
6
x
x
x
Cos
))
3
(
(
2
5
.
3
2
2
2
10
)
(
)
(
x
x
x
Cos
x
Sin
7
x
x
x
2
3
2
3
5
.
0
2
)
3
ln(
/
)
(
3
x
x
x
Cos
8
x
x
x
Sin
)
)
(
(
2
5
.
2
1
/
)
(
x
e
x
Sin
x
x
9
x
x
x
Cos
x
)
)
3
(
(
2
2
5
.
3
2
2
)
(
)
(
x
x
x
Sin
x
Cos
10
x
x
x
2
1
0
1
1
x
x
x
11
x
x
x
2
2
1
25
.
1
0
2
2
1
x
x
x
12
x
x
Cox
x
Sin
)
(
)
(
(
2
1
0
2
1
x
x
x
13
x
x
Sin )
(
1
2
.
1
0
)
(
x
x
xCos
14
x
x
Cos )
(
1
5
.
2
1
2
/
)
(
x
x
x
Sin
x
15
x
x
Sin
)
(
1
2
8
.
1
6
.
0
2
8
.
0
x
x
x
16
x
x
x
x
)
1
(
2
5
.
1
5
.
0
2
2
1
x
x
17
x
x
Cox
x
)
(
(
2
5
.
2
1
/
)
(
x
e
x
Cos
x
18
x
x
Cos
x
)
(
2
.
1
4
.
0
2
1
)
(
x
x
x
Cox
19
x
x
Cos
x
Sin
)
(
)
(
1
2
.
3
4
.
0
2
)
ln(
x
x
x
20
x
x
xCox
)
(
(
2
8
.
0
2
.
0
)
(
1
x
x
Cos
x
21
x
x
Cox
x
)
2
(
2
(
2
1
.
2
7
.
0
1
)
(
x
x
x
Sin
22
x
x
Sin
x
Cos
)
(
3
)
(
5
.
2
1
2
(
)
1
x
x
Cos
x
23
x
x
Cos
x
Sin
)
(
)
(
4
2
.
1
4
.
0
2
)
(
x
x
Cos
x
24
dx
e
x
x
2
1
.
2
7
.
0
)
2
(
x
x
x
Sin
25
dx
x
x
2
1
2
2
.
1
4
.
0
2
)
cos(
dx
x
x
105
2. Содержание отчета
1) В форме комментариев:
• Название лабораторной работы
• ФИО студента, номер группы
• № варианта
• Индивидуальное задание
2) Протокол вычислений (сессии) в Командном окне, снабженный
необходимыми комментариями.
2.3.3.
Контрольные вопросы по теме
3) Какой функцией в Scilab определяется символьное значение
определенного интеграла?
4) Назначение функции inttrap(x,y)?
5) Что возвращает функция inttrap(x,y), если y(x) – матрица?
6) Можно ли использовать функцию inttrap(x,y), если узлы по оси х -
не равноотстоящие?
7) Какая функция Scilab позволяет вычислить определенный интеграл с
заданной точностью?
8) Способы задания подынтегральной функции при вычислении
определенного интеграла с использованием функции integrate().
9) Как задать точность вычисления определенного интеграла?
26
dx
e
x
x
3
)
1
2
(
0
)
cos(
2
3
1
dx
x
27
dx
x)
(
sin
1
1
2
1
1
2
2
)
1
(
1
dx
x
28
dx
x
x
1
2
4
1
2
5
1
1
dx
x
x
29
dx
x
x
2
2
4
3
1
2
1
1
dx
x
x
30
dx
x
x
)
(
sin
)
(
cos
3
2
2
1
2
2
1
dx
e
x
e
x
x