ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 10284
Скачиваний: 94
46
1.5.10. Решение задач 7,8 контрольной работы № 1
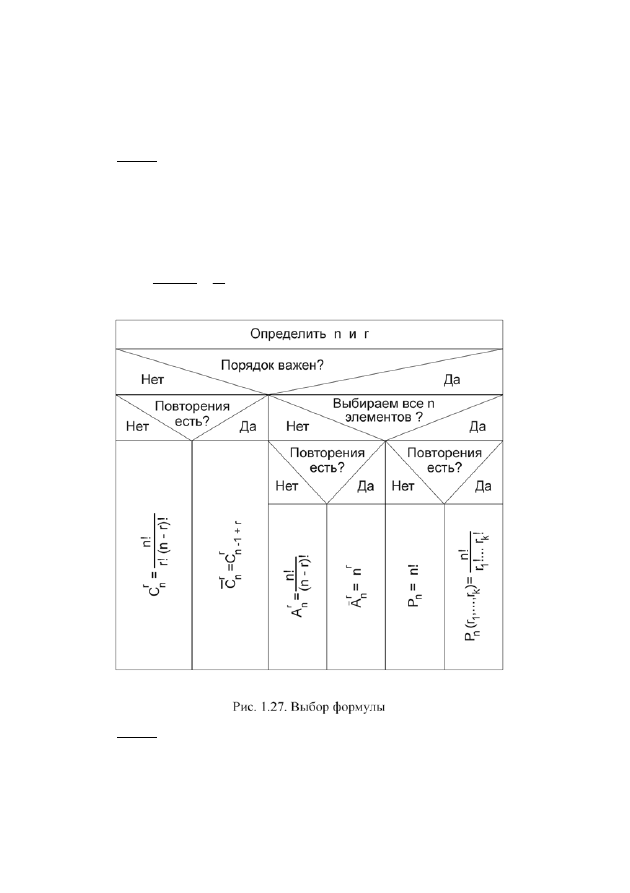
При решении задач комбинаторики рекомендуем выбирать нужную фор-
мулу, пользуясь блок-диаграммой (рис. 1.27).
Задача. В профком избрано 9 человек. Из них надо выбрать председате-
ля, его заместителя и казначея. Сколькими способами это можно сделать?
Решение. Составим список в порядке: председатель, заместитель, казна-
чей. Выбираем трех из 9 человек, т.е.
3
,
9
=
= r
n
. Порядок важен? Да, выби-
раем правую часть блок-диаграммы (рис. 1.27). Следующий вопрос: выбираем
все
n
элементов? Нет. Повторения есть? Нет. Следовательно, наша выборка –
размещение без повторений и количество таких выборок
.
504
9
8
7
!
6
!
9
)!
3
9
(
!
9
3
9
=
⋅
⋅
=
=
−
=
A
Задача. Сколькими способами 40 человек можно рассадить в три автобу-
са, если способы различаются только количеством человек в каждом автобусе?
Решение. Выстроим 40 человек в очередь и выдадим каждому билет с
номером автобуса. Получим выборку, например, такую:
1
,
2
,
,
1
,
3
,
2
,
2
,
1
,
1
…
. В

47
этой выборке 40 элементов (
40
=
r
), а значений – номеров автобусов – три
(
3
=
n
). Порядок важен? Чтобы ответить на этот вопрос, поменяем местами
двух человек в очереди и посмотрим, изменилась ли выборка. Выборка не из-
менилась, т.к. количество людей в каждом автобусе осталось прежним. Поря-
док не важен, поэтому выбираем левую часть блок-диаграммы (рис. 1.27). По-
вторения есть? Да, в нашей выборке номер автобуса может встречаться не-
сколько раз. Следовательно, выборка является сочетанием с повторениями из
3
=
n
по
40
=
r
элементов:
.
861
21
41
!
2
!
40
!
42
)!
1
3
(
!
40
)!
40
1
3
(
40
3
=
⋅
=
⋅
=
−
⋅
+
−
=
С
1.5.11. Бином Ньютона
В школе изучают формулы сокращенного умножения:
.
3
3
)
(
,
2
)
(
3
2
2
3
3
2
2
2
b
ab
b
a
a
b
a
b
ab
a
b
a
+
+
+
=
+
+
+
=
+
Бином Ньютона позволяет продолжить этот ряд формул. Раскроем скоб-
ки в следующем выражении:
…
раз
n
n
b
a
b
a
b
a
b
a
)
(
)
)(
(
)
(
+
+
+
=
+
Общий член суммы будет иметь вид
.
k
n
k
b
Ca
−
Чему равен коэффициент
C
? Он равен количеству способов, которыми можно получить слагаемое
k
n
k
b
a
−
(т.е. количеству способов, которыми можно выбрать
k
скобок с мно-
жителем
a
, а из остальных
k
n
−
скобок взять множитель
b
). Например, если
,
2
,
5
=
= k
n
то слагаемое
3
2
b
a
можем получить, выбрав множитель
a
из
первой и пятой скобки. Каков тип выборки? Порядок перечисления не важен
(выбираем сначала первую, затем пятую скобки, или, наоборот, сначала пя-
тую, затем первую – безразлично), повторяющихся элементов (одинаковых
номеров скобок) в выборке нет. Это сочетание без повторений. Количество
таких выборок равно
.
)!
(
!
!
k
n
k
n
С
k
n
−
=
Таким образом, формула бинома для произвольного натурального n име-
ет вид:
n
n
n
n
n
n
n
n
n
n
n
n
n
a
C
b
a
C
b
a
C
ab
C
b
C
b
a
+
+
+
+
+
=
+
−
−
−
−
1
1
2
2
2
1
1
0
...
)
(
или
∑
=
−
=
+
n
k
k
n
k
k
n
n
b
a
C
b
a
0
)
(
.

48
Пример. При
4
=
n
получим формулу
,
4
6
4
)
(
4
3
2
2
3
4
4
4
4
3
3
4
2
2
2
4
3
1
4
4
0
4
4
a
b
a
b
a
ab
b
a
C
b
a
C
b
a
C
ab
C
b
C
b
a
+
+
+
+
=
=
+
+
+
+
=
+
т.к.
...
;
6
)!
2
4
(
!
2
!
4
;
4
)!
1
4
(
!
1
!
4
;
1
)!
0
4
(
!
0
!
4
2
4
1
4
0
4
=
−
=
=
−
=
=
−
=
C
C
C
Проверьте правильность формулы, перемножив
3
)
(
b
a
+
на
)
(
b
a
+
.
Строгое доказательство формулы бинома Ньютона проводится методом
математической индукции.
1.5.12. Свойства биномиальных коэффициентов
Биномиальными коэффициентами являются величины
)!
(
!
!
k
n
k
n
С
k
n
−
=
,
которые выражают число сочетаний из
n
элементов по
k
. Эти величины обла-
дают следующими свойствами.
Свойство симметрии.
k
n
n
k
n
C
С
−
=
.
В формуле бинома это означает, что коэффициенты, стоящие на одина-
ковых местах от левого и правого концов формулы, равны, например:
.
15
!
4
!
2
!
6
4
6
2
6
=
⋅
=
= С
С
Действительно,
k
n
С
- это количество подмножеств, содержащих
k
эле-
ментов, множества, содержащего
n
элементов. А
k
n
n
С
−
- количество дополни-
тельных к ним подмножеств. Сколько подмножеств, столько и дополнений.
Свойство Паскаля.
.
1
1
1
−
−
−
+
=
k
n
k
n
k
n
C
C
С
Пусть
}
,
,
,
{
2
1
n
x
x
x
X
…
=
. Число
k
n
С
- это количество подмножеств из
k
элементов множества
X
. Разделим все подмножества на два класса:
1) подмножества, не содержащие элемент
1
x
, - их будет
k
n
С
1
−
;
2) подмножества, содержащие элемент
1
x
, - их будет
1
1
−
−
k
n
С
.

49
Т.к. эти классы не пересекаются, то по правилу суммы количество всех
k
-
элементных подмножеств множества
X
будет равно
.
1
1
1
−
−
−
+
k
n
k
n
C
С
На этом свойстве основано построение треугольника Паскаля (рис. 1.28),
в
n
-ой строке которого стоят коэффициенты разложения бинома
n
b
a
)
(
+
.
Свойство суммы.
.
2
...
2
1
0
n
n
n
n
n
n
C
C
C
С
=
+
+
+
+
Подставим в формулу бинома Ньютона
∑
=
−
=
+
n
k
k
n
k
k
n
n
b
a
C
b
a
0
)
(
значения
1
,
1
=
=
b
a
. Получим
.
1
1
2
0
0
∑
∑
=
=
−
=
=
n
k
k
n
n
k
k
n
k
k
n
n
C
C
Заметим, что с точки зрения теории множеств сумма
n
n
n
n
C
C
С
+
+
+
...
1
0
выражает количество всех подмножеств
n
-элементного множества. По теореме
о мощности булеана (см. 1.4.6) это количество равно
n
2
.
Свойство разности.
.
0
)
1
(
...
3
2
1
0
=
−
+
−
+
−
n
n
n
n
n
n
n
C
С
C
C
С
Положим в формуле бинома Ньютона
1
,
1
−
=
=
b
a
. Получим в левой
части
0
)
1
1
(
=
−
n
, а в правой – биномиальные коэффициенты с чередующи-
мися знаками, что и доказывает свойство.
Последнее свойство удобнее записать, перенеся все коэффициенты с от-
рицательными знаками в левую часть формулы:
...,
...
2
0
5
3
1
+
+
=
+
+
+
n
n
n
n
n
C
C
С
C
C

50
тогда свойство легко запоминается в словесной формулировке: “ сумма бино-
миальных коэффициентов с нечетными номерами равна сумме биномиальных
коэффициентов с четными номерами”.
Задача. Найти член разложения бинома
,
1
4
n
x
x
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
не содержащий
x
,
если сумма биномиальных коэффициентов с нечетными номерами равна 512.
Решение. По свойству разности сумма биномиальных коэффициентов с
четными номерами также равна 512, значит, сумма всех коэффициентов равна
512+512=1024. Но по свойству суммы это число равно
1024
2
2
10
=
=
n
. По-
этому
10
=
n
. Запишем общий член разложения бинома и преобразуем его:
;
,...,
1
,
0
,
1
4
4
4
1
n
k
x
C
x
x
C
b
a
C
T
k
n
k
k
n
k
n
k
k
n
k
n
k
k
n
k
=
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
=
+
−
−
−
+
при
10
=
n
получим:
.
,...,
1
,
0
,
40
5
10
1
n
k
x
C
T
k
k
k
=
=
−
+
Член разложения
1
+
k
T
не содержит
x
, если
0
40
5
=
−
k
, т.е.
8
=
k
.
Итак,
девятый
член
разложения
не
содержит
x
и
равен
.
45
)!
8
10
(
!
8
!
10
8
10
9
=
−
=
= C
T
Свойство максимума. Если степень бинома
n
– четное число, то среди
биномиальных коэффициентов есть один максимальный при
2
n
k
=
. Если сте-
пень бинома нечетное число, то максимальное значение достигается для двух
биномиальных коэффициентов при
2
1
1
−
=
n
k
и
.
2
1
2
+
=
n
k
Так, при
4
=
n
максимальным является коэффициент
6
2
4
=
C
, а при
3
=
n
максимальное значение равно
3
2
3
1
3
=
=
C
C
(рис. 1.28).
1.5.13. Контрольные вопросы и упражнения
1.
Выборка, среди элементов которой нет одинаковых, а порядок записи
элементов важен, является ______________________ .
2.
Выборка, среди элементов которой нет одинаковых, а порядок записи
элементов безразличен, является ________________________ .
3.
Количество размещений с повторениями из
n
элементов по
r
элемен-
тов определяется по формуле