ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 10281
Скачиваний: 94

41
Упорядоченный набор элементов, среди которых могут быть одинако-
вые, называется размещением с повторениями. Количество таких выборок
обозначается
A
r
n
.
Пример. Составляя всевозможные четырехзначные телефонные номера
из десяти цифр, мы получаем размещения с повторениями из 10 по 4, т.к. в
телефонном номере могут встретиться одинаковые цифры, порядок записи
цифр важен.
Неупорядоченный набор элементов, среди которых нет повторяющихся,
называется сочетанием из
n
элементов по
r
. Количество сочетаний обознача-
ется
С
r
n
.
Пример. Из восьми человек нужно выбрать троих, чтобы вручить им ло-
паты для уборки снега. Здесь порядок отбора не важен, и одному человеку
вручить две лопаты не удастся – имеем сочетание из восьми по три.
Неупорядоченный набор элементов, среди которых могут быть одинако-
вые, называется сочетанием с повторениями. Количество таких выборок
обозначается
С
r
n
.
Пример. С трех различных негативов хотим напечатать пять фотографий.
Здесь порядок печати не важен, а в полученном наборе обязательно будут
одинаковые фотографии – это сочетания с повторениями из трех элементов по
пять.
1.5.3. Основные правила комбинаторики
В 1.4.6 мы доказывали теоремы о свойствах конечных множеств. Именно
они, лишь в другой формулировке, используются при выводе формул комби-
наторики как основные правила.
Правило суммы. Если элемент
a
может быть выбран
m
способами, а
элемент
b
другими
k
способами, то выбор одного из этих элементов –
a
или
b
может быть сделан
m+k
способами.
Пример. На конюшне четыре лошади и два пони. Сколько возможностей
выбрать себе скакуна? Здесь используем правило суммы: выбираем один эле-
мент из двух множеств (лошадь или пони)
6
2
4
=
+
способами.
Правило произведения. Если элемент
a
может быть выбран m способа-
ми, а после этого элемент
b
выбирается
k
способами, то выбор пары элементов
)
,
(
b
a
в заданном порядке может быть произведен
k
m
⋅
способами.
Пример. Пару лыж можно выбрать шестью способами, пару ботинок –
тремя. Сколькими способами можно выбрать лыжи с ботинками? Здесь выби-
раем пару элементов (лыжи, ботинки) – всего
18
3
6
=
⋅
способов.
Правило включения-исключения. Если свойством
S
обладает
m
элемен-
тов, а свойством
P
обладает
k
элементов, то свойством
S
или
P
обладает

42
l
k
m
−
+
элементов, где
l
– количество элементов, обладающих одновременно
и свойством
S
, и свойством
P
.
Пример. На полке стоят банки с компотом из яблок и груш. В десяти
банках есть яблоки, в шести – груши, в трех – и яблоки, и груши. Сколько все-
го банок на полке? Здесь
3
,
6
,
10
=
=
=
l
k
m
, т.е. всего на полке
13
3
6
10
=
−
+
=
−
+
l
k
m
банок.
1.5.4. Размещения с повторениями
Задача. Определить количество всех упорядоченных наборов
)
,
,
,
(
2
1
r
x
x
x
…
длины
r
, которые можно составить из элементов множества
X
(
n
X
=
), если выбор каждого элемента
r
i
x
i
,
,
2
,
1
,
…
=
, производится из
всего множества
X
.
Упорядоченный набор
)
,
,
,
(
2
1
r
x
x
x
…
– это элемент декартова произве-
дения
r
X
X
X
X
=
×
×
×
…
, состоящего из
r
одинаковых множителей
X
. По
правилу произведения количество элементов множества
r
X
равно
r
r
r
n
X
X
=
=
. Мы вывели формулу
r
r
n
n
A
=
.
Пример. Сколько четырехзначных номеров можно составить, если ис-
пользовать все десять цифр?
Здесь
4
,
10
=
=
r
n
, и количество телефонных номеров равно
.
10000
10
4
4
10
=
=
A
1.5.5. Размещения без повторений
Задача. Сколько упорядоченных наборов
)
,
,
,
(
2
1
r
x
x
x
…
можно соста-
вить из
n
элементов множества
X
, если все элементы набора различны?
Первый элемент
1
x
можно выбрать
n
способами. Если первый элемент
уже выбран, то второй элемент
2
x
можно выбрать лишь
1
−
n
способами, а
если уже выбран
1
−
r
элемент
1
2
1
,
,
,
−
r
x
x
x
…
, то элемент
r
x
можно выбрать
1
)
1
(
+
−
=
−
−
r
n
r
n
способами (повторение уже выбранного элемента не
допускается). По правилу произведения получаем
).
1
(
...
)
1
(
+
−
⋅
⋅
−
⋅
=
r
n
n
n
A
r
n
Эта формула записывается иначе с использованием обозначения
n
n
⋅
⋅
⋅
=
…
2
1
!
. Так как
,
!
1
2
...
)
(
)
1
(
...
)
1
(
)!
(
n
r
n
r
n
n
n
r
n
A
r
n
=
⋅
⋅
⋅
−
⋅
+
−
⋅
⋅
−
⋅
=
−
⋅
то

43
)!
(
!
r
n
n
A
r
n
−
=
.
Пример. Сколько может быть различных списков победителей олимпиа-
ды (первое, второе, третье место), если участвовало 20 человек?
Здесь
3
,
20
=
=
r
n
, искомым является число
.
6840
18
19
20
!
17
!
20
)!
3
20
(
!
20
3
20
=
⋅
⋅
=
=
−
=
A
1.5.6. Перестановки без повторений
Рассмотрим частный случай размещения без повторений: если
r
n
=
, то
в размещении участвуют все элементы множества
X
, т.е. выборки имеют оди-
наковый состав и отличаются друг от друга только порядком элементов. Такие
выборки называются перестановками. Количество перестановок из n элемен-
тов обозначают
n
P
:
!
1
...
)
1
(
)
1
(
...
)
1
(
n
n
n
n
n
n
n
A
P
n
n
n
=
⋅
⋅
−
⋅
=
+
−
⋅
⋅
−
⋅
=
=
Пример. Сколькими способами можно выстроить очередь в кассу, если
хотят получить зарплату шесть человек?
720
6
2
1
!
6
6
=
⋅
⋅
⋅
=
=
…
P
.
1.5.7. Перестановки с повторениями
Пусть
множество
X
состоит
из
k
различных
элементов:
}
,
,
,
{
2
1
k
x
x
x
X
…
=
. Перестановкой с повторениями состава
)
,
,
,
(
2
1
k
r
r
r
…
будем называть упорядоченный набор длины
k
r
r
r
n
+
+
+
=
…
2
1
, в котором
элемент
i
x
встречается
i
r
раз
)
,
,
2
,
1
(
k
i
…
=
. Количество таких перестановок
обозначается
)
,
,
,
(
2
1
k
n
r
r
r
P
…
.
Пример. Из букв
}
,
,
{
c
b
a
запишем перестановку с повторением состава
)
1
,
2
,
2
(
. Ее длина
5
1
2
2
=
+
+
=
n
, причем буква
a
входит 2 раза,
b
– 2 раза,
c
– один раз. Такой перестановкой будет, например,
)
,
,
,
,
(
c
b
a
b
a
или
)
,
,
,
,
(
b
a
a
c
b
.
Выведем формулу количества перестановок с повторениями. Занумеруем
все одинаковые элементы, входящие в перестановку, различными индексами,
т.е. вместо перестановки
)
,
,
,
,
(
c
b
a
b
a
получим
)
,
,
,
,
(
2
2
1
1
c
b
a
b
a
. Теперь все
элементы перестановки различны, а количество таких перестановок равно
)!
(
!
2
1
k
r
r
r
n
+
+
+
=
…
. Первый элемент встречается в выборке
1
r
раз. Уберем
индексы у первого элемента (в нашем примере получим перестановку

44
)
,
,
,
,
(
2
1
c
b
a
b
a
), при этом число различных перестановок уменьшится в
!
1
r
раз, т.к. при изменении порядка одинаковых элементов наша выборка не изме-
нится. Уберем индексы у второго элемента – число перестановок уменьшится
в
!
2
r
раз. И так далее, до элемента с номером
k
– число перестановок умень-
шится в
!
k
r
раз. Получим формулу
.
!
...
!
!
!
)
,...,
,
(
2
1
2
1
k
k
n
r
r
r
n
r
r
r
P
⋅
⋅
⋅
=
Пример. Сколько различных “слов” можно получить, переставляя буквы
слова “передача” ?
В этом слове буквы “е” и “а” встречаются два раза, остальные по одному
разу. Речь идет о перестановке с повторениями состава
)
1
,
1
,
1
,
1
,
2
,
2
(
длины
8
1
1
1
1
2
2
=
+
+
+
+
+
=
n
. Количество таких перестановок равно
10080
2
!
7
!
1
!
1
!
1
!
1
!
2
!
2
!
8
)
1
,
1
,
1
,
1
,
2
,
2
(
8
=
⋅
=
⋅
⋅
⋅
⋅
⋅
=
P
.
1.5.8. Сочетания
Задача. Сколько различных множеств из
r
элементов можно составить из
множества, содержащего
n
элементов?
Будем составлять вначале упорядоченные наборы по
r
элементов в каж-
дом. Количество таких наборов (это размещения из
n
элементов по
r
) равно
)!
(
!
r
n
n
A
r
n
−
=
. Теперь учитываем, что порядок записи элементов нам безраз-
личен. При этом из
!
r
различных размещений, отличающихся только поряд-
ком элементов, получим одно сочетание. Например, два различных размеще-
ния
)
,
(
b
a
и
)
,
( a
b
из двух элементов соответствуют одному сочетанию
}
,
{ b
a
. Таким образом, число сочетаний
r
n
С
в
!
r
раз меньше числа разме-
щений
r
n
A
:
.
)!
(
!
!
!
r
n
r
n
r
A
С
r
n
r
n
−
=
=
Пример. Количество способов, которыми мы можем выбрать из восьми
дворников троих равно
.
56
!
5
!
3
!
8
)!
3
8
(
!
3
!
8
3
8
=
⋅
=
−
=
С
45
1.5.9. Сочетания с повторениями
Задача. Найти количество
r
n
С
сочетаний с повторениями из
n
предметов
по r.
Рассмотрим вывод формулы на примере с фотографиями (см. 1.5.2).
Имеется n типов предметов (
3
=
n
негатива). Нужно составить набор из
r
предметов (
5
=
r
фотографий). Наборы различаются своим составом, а не
порядком элементов. Например, разными будут наборы состава
)
1
,
1
,
3
(
и
)
4
,
0
,
1
(
– один содержит три фотографии с первого негатива и по одной со
второго и с третьего, а другой – одну с первого и четыре с третьего. Разложим
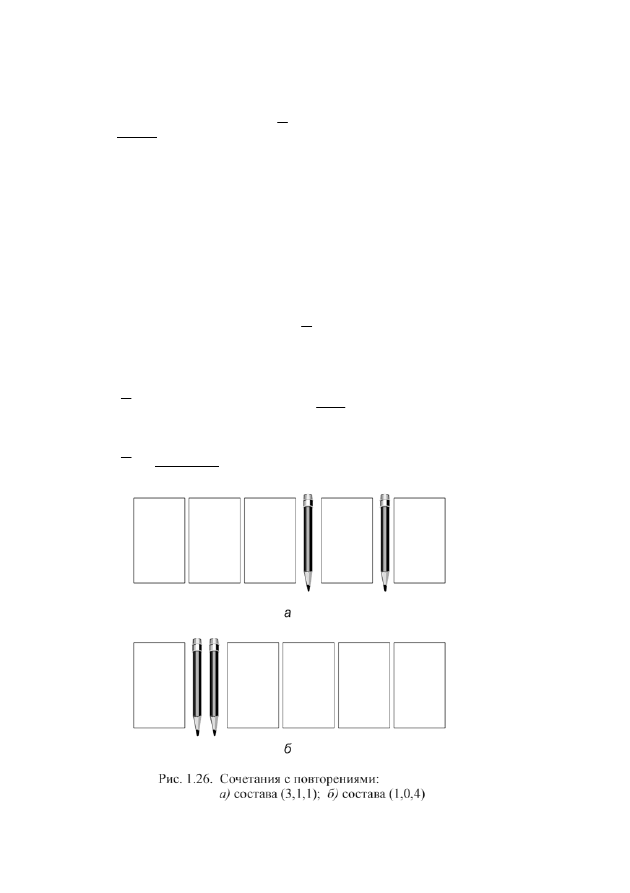
эти наборы на столе, разделяя фотографии разного типа карандашами (рис.
1.26). Карандашей нам понадобится
2
1
3
1
=
−
=
−
n
, а фотографий
5
=
r
. Мы
будем получать различные сочетания с повторениями, переставляя между со-
бой эти
r
n
+
− )
1
(
предметов, т.е.
)
,
1
(
1
r
n
P
С
r
n
r
n
−
=
+
−
число сочетаний с
повторениями из n предметов по
r
равно числу перестановок с повторениями
длины
r
n
+
−1
состава
)
,
1
(
r
n
−
. В нашем примере
.
21
!
5
!
2
!
7
)
5
,
2
(
)
5
,
1
3
(
7
5
1
3
5
3
=
⋅
=
=
−
=
+
−
P
P
С
Иначе формулу сочетаний с повторениями можно записать
.
!
)!
1
(
)!
1
(
1
r
r
n
r
n
C
r
n
r
n
С
+
−
=
⋅
−
+
−
=