ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.11.2020
Просмотров: 2493
Скачиваний: 17
122
Глава 4. Статистические методы в политическом анализе
Из таблицы хорошо видно, что гамма (как и другие меры связи по
рядковых переменных) фиксирует соответствия и инверсии именно
рангов переменных, а не их значений. Так, в левом столбце при у = 1
абсолютные значения переменных не совпадают ни разу.
4.3. Корреляционный анализ
Корреляционный анализ является одним из наиболее широко ис
пользуемых статистических методов, в частности и в рамках полити
ческой науки. При своей относительной простоте он может быть весь
ма полезен как для тестирования имеющихся гипотез, так и в
поисковом исследовании, когда предположения о связях и взаимоза
висимостях только формируются. Умение работать с данной статис
тической техникой важно и в силу того, что она используется как со
ставная часть более сложных, комплексных методов, в том числе
факторного анализа, некоторых версий кластер-анализа и др.
Целью корреляционного анализа является измерение стати
стической взаимозависимости между двумя или более переменными.
В слу
чае, если исследуется связь двух переменных, корреляционный анализ
будет
парным;
если число переменных более двух —
множественным.
Следует подчеркнуть, что переменные в корреляционном анализе как
бы «равноправны» — они не делятся на зависимые и независимые (объ
ясняемые и объясняющие). Мы рассматриваем именно взаимозависи
мость (взаимосвязь) переменных, а не влияние одной из них на другую.
Понятие «корреляционный анализ» фактически объединяет несколь
ко методов анализа статистической связи. В фокусе нашего внимания
будет находиться наиболее распространенный из них —
метод Пирсона
(Pearson)
1
. Его применение ограничено следующими условиями:
•переменные должны быть измерены, как минимум, на интер
вальном уровне;
• связь между переменными должна носить л и н е й н ы й характер,
т.е. фиксироваться прямой линией. При наличии нелинейной связи
корреляционный анализ Пирсона, скорее всего, не даст ее адекватно
го отображения;
1
Коэффициент Пирсона вычисляется по следующей формуле:
где
Xj
и
у/ —
значения двух переменных,
х
и
у
— их средние значения,
s
x
и
s
y
—
их стан
дартные отклонения;
п
— количество пар значений.
4.3. Корреляционный анализ
123
•анализируемые переменные должны быть распределены нор
мально (или, во всяком случае, приближаться к нормальному распре
делению).
Корреляционный анализ фиксирует две характеристики статисти
ческой взаимосвязи между переменными:
• направленность
связи. Как уже говорилось, по направленности
связь бывает прямая (положительная) и обратная (отрицательная);
• интенсивность
(плотность, теснота) связи. Эта характеристика
определяет наши возможности по предсказанию значений одной пе
ременной на основании значений другой.
Чтобы более наглядно представить себе особенности корреляцион
ного анализа, обратимся к примеру из сферы исследования электо
ральных процессов. Предположим, мы проводим сравнительный ана
лиз электората двух политических партий либеральной ориентации —
Союза правых сил и «Яблока». Наша задача — понять, существует ли
общность электората С П С и «Яблока» в территориальном разрезе и
насколько она значима. Для этого мы можем, например, взять данные
электоральной статистики, характеризующие уровень поддержки этих
партий, в разрезе данных избирательных комиссий субъектов Федера
ции. Проще говоря, мы смотрим на проценты, полученные С П С и
«Яблоком» по регионам России. Ниже приводятся данные по выборам
депутатов Государственной думы 1999 г. (количество регионов 88, по
скольку выборы в Чеченской Республике не проводились)
1
.
Случай
Переменные (%)
Случай
«Яблоко»
С П С
Республика Адыгея
4,63
3,92
Республика Алтай
3,38
5,40
Республика Башкортостан
3,95
6,04
Республика Бурятия
3,14
8,36
Республика Дагестан
0,39
1,22
Республика Ингушетия
2,89
0,38
Кабардино-Балкарская Республика
1,38
1,30
Республика Калмыкия
3,07
3,80
Карачаево-Черкесская Республика
4,17
2,94
Республика Карелия
9,66
10,25
Республика Коми
8,91
9,95
Республика Марий Эл
4,68
7.24
И т.д. (всего 88 случаев)
1
Здесь и далее результаты выборов взяты из (или рассчитаны на основе) официаль
ных данных Ц И К РФ или ее территориальных подразделений.
(24
Глава 4. Статистические методы в политическом анализе
Таким образом, у нас есть две переменные — «поддержка С П С в
1999 г.» и «поддержка " Я б л о к а " в 1999 г.», п р о с т е й ш и м образом
о п е р а ц и о н а л и з и р о в а н н ы е через процент голосов, п о д а н н ы х за эти
партии, от числа избирателей, п р и н я в ш и х участие в голосовании
на федеральных парламентских выборах 1999 г. В качестве случаев
выступают соответствующие д а н н ы е , о б о б щ е н н ы е на уровне реги
онов Р Ф .
Далее, в нашем распоряжении есть методический прием, кото
рый является одним из основных в статистике, —
геометрическое
представление.
Геометрическим представлением называют представ
ление случая как точки в условном пространстве, формируемом
«осями» — п е р е м е н н ы м и . В нашем примере мы можем представить
каждый регион как точку в двухмерном пространстве голосований за
правые партии. Ось
X
формирует признак «поддержка С П С » , ось
Y—
«поддержка "Яблока"» (или наоборот; для корреляционного
анализа это неважно в силу неразличения зависимых и независимых
переменных). «Координатами» региона будут: по оси
X —
значение
переменной «поддержка СПС» (процент, набранный в регионе дан
ной партией); по оси
Y—
значение переменной «поддержка "Ябло
ка"». Так, Республика Адыгея будет иметь координаты (3,92; 4,63),
Республика Алтай — (3,38; 5,4) и т.д. Осуществив геометрическое
представление всех случаев, мы получаем
диаграмму рассеяния,
или
корреляционное поле.
Даже сугубо визуальный анализ диаграммы р а с с е я н и я наводит
на мысль, что совокупность точек м о ж н о расположить вдоль неко
торой условной п р я м о й , называемой
линией регрессии.
Математи-
4.3. К о р р е л я ц и о н н ы й анализ
125
чески л и н и я регрессии строится методом н а и м е н ь ш и х квадратов
(высчитывается такое положение л и н и и , при котором сумма квад
ратов р а с с т о я н и й от наблюдаемых точек до п р я м о й является мини
мальной).
Интенсивность связи будет зависеть от того, насколько тесно
точки (случаи) расположены вдоль л и н и и регрессии. В
коэффициен
те корреляции
(обозначается
г),
который и является числовым ре
зультатом корреляционного анализа, плотность колеблется от 0 до 1.
П р и этом чем ближе значение к о э ф ф и ц и е н т а к 1, тем плотнее
связь; чем ближе значение к 0, тем связь слабее. Так, при
г
= 1 связь
приобретает характер ф у н к ц и о н а л ь н о й — все точки «ложатся» на
одну прямую. П р и
г
= 0, ф и к с и р у ю щ е м полное отсутствие связи,
построение л и н и и регрессии становится н е в о з м о ж н ы м . В нашем
примере
г =
0,62, что свидетельствует о наличии з н а ч и м о й статис
тической связи (подробнее об и н т е р п р е т а ц и и к о э ф ф и ц и е н т а кор
р е л я ц и и см. н и ж е ) .
Тип связи определяется наклоном линии регрессии. В коэффици
енте корреляции существует всего два значения типа связи: обратная
(знак «-») и прямая (отсутствие знака, так как знак «+» традиционно
не записывается). В нашем примере связь прямая. Соответственно,
итоговый результат анализа 0,62.
Сегодня коэффициент корреляции Пирсона можно легко подсчи
тать с помощью всех компьютерных пакетов программ статистическо
го анализа (SPSS, Statistica, NCSS и др.) и даже в широко распростра
ненной программе Excel (надстройка «анализ данных»). Настоятельно
рекомендуем пользоваться профессиональными пакетами, так как они
позволяют визуально оценить корреляционное поле.
Почему важна визуальная оценка геометрического представления
данных? Во-первых, мы должны убедиться, что связь линейна по
форме, а здесь самый простой и эффективный метод — именно зри
тельная оценка. Напомним, что в случае ярко выраженной нелиней
ности связи вычисление к о э ф ф и ц и е н т а корреляции окажется беспо
лезным. Во-вторых, визуальная оценка позволяет найти в данных
выбросы, т.е. нетипичные, резко выделяющиеся случаи.
Вернемся к нашему примеру с двумя партиями. Внимательно
глядя на диаграмму рассеяния, мы замечаем по меньшей мере один
н е т и п и ч н ы й случай, лежащий я в н о в стороне от «общей магистра
ли», т е н д е н ц и и связи переменных. Это точка, представляющая дан
ные по С а м а р с к о й области. Хотя и в меньшей степени, но тоже
н е т и п и ч н о положение Томской, Нижегородской областей и Санкт-
Петербурга.
1 2 6
Глава 4. Статистические методы в политическом анализе
Можно скорректировать данные анализа, удалив сильно отклоня
ющиеся наблюдения, т.е. произведя «чистку выбросов». В силу специ
ф и к и вычисления л и н и и регрессии, связанной с подсчетом суммы
квадратов расстояний, даже единичный выброс может существенно
исказить общую картину.
Удалив только один из 88 случаев — Самарскую область, — мы по
лучим значение коэффициента корреляции, отличное от полученно
го ранее: 0,73 по сравнению с 0,62. Плотность связи усилилась более
чем на 0,1 — это весьма и весьма существенно. Избавившись отточек,
соответствующих Санкт-Петербургу, Томской и Нижегородской об
ластям, получим еще более высокую плотность: 0,77.
Впрочем, чисткой выбросов не следует увлекаться: сокращая ко
личество случаев, мы понижаем общий уровень статистического до
верия к полученным результатам. К сожалению, общепринятых кри
териев определения выбросов не существует, и здесь многое зависит
от добросовестности исследователя. Лучший способ — содержательно
понять, с чем связано наличие «выброса». Так, в нашем примере не
типичное положение Самарской области в признаковом простран
стве связано с тем, что в 1999 г. одним из активных лидеров правых
был глава региона К. Титов. Соответственно, высокий результат С П С
в регионе был обусловлен не только поддержкой партии как таковой,
но и поддержкой губернатора.
Возвратимся к нашему исследованию. Мы выяснили, что голосо
вание за С П С и «Яблоко» довольно плотно коррелирует между собой
4.3. Корреляционный анализ
127
на массиве данных, взятых в территориальном разрезе. Логично пред
положить, что в основе этой связи лежит некий фактор или комплекс
факторов, который мы пока непосредственно не учитывали. Исследуя
данные электоральной статистики разного уровня, нетрудно заме
тить, что обе партии демонстрируют лучшие результаты в городах и
худшие — в сельских районах. Мы можем выдвинуть гипотезу, что од
ним из факторов, опосредующих связь между переменными, является
уровень урбанизации территорий. Этот признак проще всего опера-
ционализировать через переменную «доля сельского населения» или
«доля городского населения»
1
. Такая статистика существует по каждо
му субъекту Федерации.
Теперь в наших исходных данных появляется третья переменная —
пусть это будет «доля сельского населения»
2
.
Случай
П е р е м е н н ы е (%)
«Яблоко»
С П С
Сел. нас.
Республика Адыгея
4,63
3,92
46
Республика Алтай
3,38
5,40
76
Республика Б а ш к о р т о с т а н
3,95
6,04
36
И т.д. (всего 88 случаев)
Чисто технически мы можем вычислять каждый парный коэффици
ент корреляции отдельно, но удобнее сразу получить
матрицу интер
корреляций
(матрицу парных корреляций). Матрица обладает диаго
нальной симметрией. В нашем случае она будет выглядеть следующим
образом:
С П С
«Яблоко»
Сел. нас.
С П С
1
0,62
- 0 , 6 1
«Яблоко»
0,62
1
- 0 , 5 5
Гор. нас.
- 0 , 6 1
- 0 , 5 5
1
Мы получили статистически значимые коэффициенты корреля
ции, подтверждающие выдвинутую нами гипотезу. Так, доля город-
1
Объективно гораздо точнее будут результаты, полученные с помощью более ди
в е р с и ф и ц и р о в а н н ы х статистических данных. Так, полезно выделить в отдельную груп
пу поселки городского типа, жители которых ф о р м а л ь н о принадлежат к городскому на
селению, а на деле зачастую демонстрируют электоральное поведение, свойственное
жителям сельских территорий.
2
П о д а н н ы м Всероссийской переписи населения 1989 г.
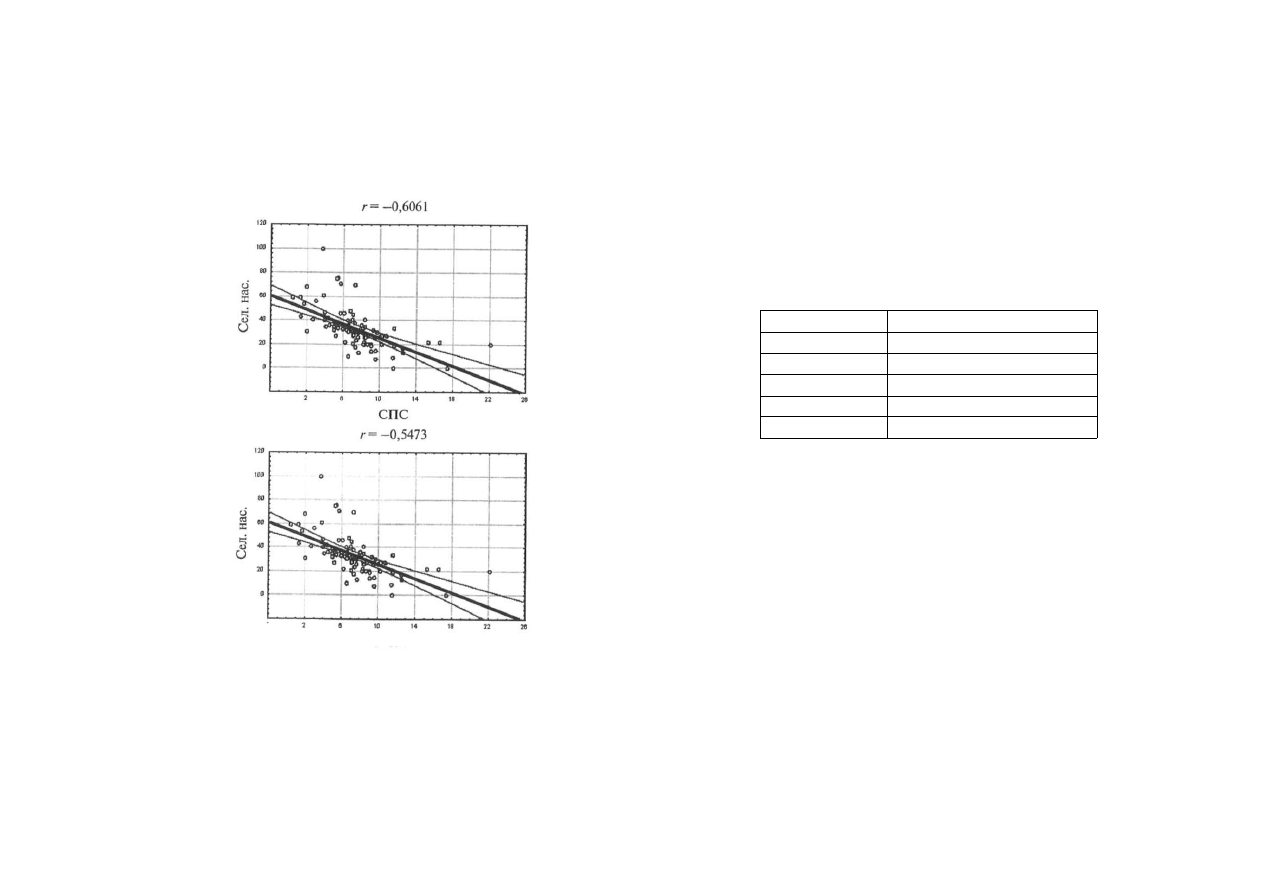
128
Глава 4. Статистические методы в политическом анализе
ского населения оказалась отрицательно связанной как с поддерж
кой С П С
(г=
-0,61), так и с поддержкой «Яблока»
(г=
- 0 , 5 5
!
) . Мож
но заметить, что переменная «поддержка СПС» более чувствительна
к фактору урбанизации по сравнению с переменной «поддержка
"Яблока"».
«Яблоко»
В этом примере мы уже начинаем мыслить в категориях влияния
одной переменной на другую. Строго говоря, и это отмечено выше,
корреляционный анализ не различает зависимых и независимых пе
ременных, фиксируя лишь их взаимную статистическую связь. В то
же время содержательно мы понимаем, что именно принадлежность
Следует отметить, что после чистки выбросов (см. диаграммы рассеяния) связь бы
ла бы еще плотнее. Так, после удаления двух выбросов (Самарская область и Усть-Ордын
ский Бурятский АО) плотность коэффициента для С П С увеличивается до - 0 , 6 5 .
4.3. К о р р е л я ц и о н н ы й анализ
129
избирателей к городскому или сельскому населению влияет на их
электоральный выбор, а никак не наоборот.
Интерпретация интенсивности связи
Мы подошли к проблеме интерпретации интенсивности связи на ос
нове значения коэффициента корреляции Пирсона. Определенного
жесткого правила здесь не существует; скорее речь идет о совокупном
опыте, накопленном в процессе статистических исследований. Тра
диционной можно считать следующую схему интерпретации данного
коэффициента:
Значение
Интерпретация
Д о 0,2
О ч е н ь слабая корреляция
До 0,5
Слабая корреляция
Д о 0,7
С р е д н я я корреляция
Д о 0,9
Высокая корреляция
С в ы ш е 0,9
О ч е н ь высокая корреляция
Необходимо отметить, что подобный вариант интерпретации
плотности к о э ф ф и ц и е н т а к о р р е л я ц и и п р и м е н и м в науках, в гораз
до большей степени о п и р а ю щ и х с я на количественные данные, не
жели наука политическая ( н а п р и м е р , в э к о н о м и к е ) . В эмпиричес
ких исследованиях политики д о в о л ь н о редко можно обнаружить
г >
0,7; к о э ф ф и ц и е н т же со значением 0,9 — случай просто уникаль
н ы й . Это связано прежде всего с особенностями мотивации поли
тического поведения — с л о ж н о й , многофакторной, нередко ирра
циональной. Ясно, что такое сложное явление, как голосование за
определенную политическую партию, не может целиком подчи
няться одному или даже двум факторам. Поэтому применительно к
политическим исследованиям предлагаем несколько смягченную
схему интерпретации:
• 0,4 >
г
> 0,3 — слабая корреляция;
• 0,6 >
г
> 0,4 — средняя корреляция;
• г
> 0,7 — сильная корреляция.
Существует еще одна полезная процедура, позволяющая оце
нить значимость к о э ф ф и ц и е н т а корреляции в процессе вычисле
н и я
коэффициента детерминации,
который представляет собой
г,
возведенный в квадрат
(г
2
).
С м ы с л процедуры состоит в том, что
при возведении в квадрат н и з к и е к о э ф ф и ц и е н т ы потеряют «в весе»
9 - 3863
130
Глава 4. Статистические методы в политическом анализе
гораздо сильнее, чем высокие. Так, 0,9
2
= 0,81 (значение снижается
всего на 0,09); 0,5
2
= 0,25 (здесь мы теряем уже половину значения);
0,3
2
= 0,09 (более чем трехкратная «потеря веса»). Когда речь идет о
переменных, которые мы можем содержательно интерпретировать
как «определяющие» и «определяемые», значение
г
2
будет показы
вать долю случаев, которые объясняет определяющая переменная.
В нашем примере к о э ф ф и ц и е н т корреляции между переменными
«поддержка С П С » и «доля сельского населения» после чистки вы
бросов составил —0,65. К о э ф ф и ц и е н т детерминации составляет со
ответственно - 0 , 6 5
2
= 0,42. Несколько упрощая реальное положе
ние дел, мы можем утверждать, что фактор урбанизации объясняет
примерно 40% вариации переменной «голосование за СПС» по ре
гионам России в 1999 г.
Использование корреляционного анализа для выявления динамики связи
переменных во времени
К о р р е л я ц и о н н ы й анализ можно использовать не только для обна
ружения связи между переменными, но и для о ц е н к и изменения
этой связи во времени. Так, при изучении проблемы электоральной
активности в регионах России необходимо было убедиться в том,
что уровень активности избирателей является некой стабильной ха
рактеристикой электоральной культуры российских территорий.
Имеются в виду, разумеется, не абсолютные показатели, которые
существенно колеблются от выборов к выборам. Речь идет об устой
чивости различий в уровне активности избирателей различных ре
гионов России.
Устойчивость пропорционального распределения явки по субъ
ектам Федерации достаточно просто проверяется методом корреля
ционного анализа. Приводимая ниже матрица парных корреляций
электоральной активности на федеральных выборах 1991—2004 гг.
довольно четко демонстрирует существующую тенденцию. Статис
тическая связь наиболее сильна внутри одного электорального цик
ла ( 1 9 9 1 - 1 9 9 3 ; 1995-1996; 1999-2000; 2003-2004), между двумя
близкими по времени циклами она несколько слабеет, а по мере уда
ления электоральных циклов стремится к затуханию
1
.
См.:
Ахременко, А. С.
Электоральное участие и абсентеизм в р о с с и й с к и х реги
онах: з а к о н о м е р н о с т и и т е н д е н ц и и // Вестник МГУ. Сер. 12. П о л и т и ч е с к и е науки.
2005. № 3.
4.3. Корреляционный анализ
131
1991
1993
1995
19961
1999
2000
2003
2004
1991
1
1993
0,83
1
1995
0,52
0,66
1
1996
0,43
0,47
0,76
1
1999
0,14
0,26
0,61
0,56
1
2000
0,13
0,15
0,34
0,47
0,74
1
2003
0,04
0,13
0,36
0,38
0,81
0,75
1
2004
0,04
0,10
0,11
0,21
0,55
0,66
0,73
1
Отметим, что внутри каждого электорального цикла плотность
корреляции превышает 0,7 (1991-1993:
г=
0,83; 1995-1996: г = 0,76;
1999—2000:
г
= 0,74; 2003—2004:
г=
0,73). На максимальной времен
ной дистанции — между президентскими и парламентскими выбора
ми 1991 — 1993 и 2003—2004 гг. — связи нет никакой, коэффициенты
не превышают 0,1. В то же время затухание связи во времени проис
ходит медленно. Так, обращает на себя внимание наличие связи, хоть
и неплотной, между уровнем электоральной активности на парла
ментских выборах 1995 и 2003 гг.
(г=
0,36). Тот факт, что определен
ная преемственность обнаруживается на протяжении восьми лет, в те
чение которых происходит серьезнейшее «переформатирование»
политического режима и системы федеративных отношений, свиде
тельствует о высокой устойчивости распределения уровня явки по
российским регионам. Таким образом, мы имеем основания считать
уровень активности/абсентеизма одной из составляющих электораль
ной культуры территорий.
Другие коэффициенты корреляции
Как было о т м е ч е н о , к о э ф ф и ц и е н т корреляции Пирсона является
наиболее р а с п р о с т р а н е н н ы м критерием связи интервальных и
нормально распределенных переменных. Но что делать, если мы
имеем п е р е м е н н ы е , существенно о т к л о н я ю щ и е с я от нормального
распределения? Или переменные не интервальные, но при этом
являются м е т р и ч е с к и м и (порядковые переменные с большим чис
лом категорий)?
1
Здесь рассматривается значение явки для первого тура президентских выборов
1996 г. Проблема к о л е б а н и й явки от первого ко второму туру анализируется отдельно.
9'