Файл: Обоснование метода математического прогнозирования несчастных случаев и профессиональных заболеваний.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 276
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
-
Вычисляются значения1 2 3 4 5 6 7 8 9
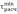
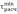 ,
, 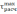
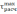 отклонений крайних значений случайной величины хmin, хmax от ее среднего значения
отклонений крайних значений случайной величины хmin, хmax от ее среднего значения 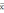
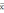 с учетом разброса
с учетом разброса 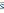
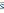 значений случайной величины x в выборке по следующим формулам:
значений случайной величины x в выборке по следующим формулам: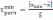
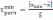 ,
, 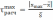
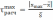 . (5)
. (5)Среднее значение опытных данных
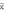
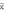 вычисляется по исходной совокупности объемом m по формуле:
вычисляется по исходной совокупности объемом m по формуле: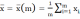
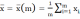 (6)
(6)Среднее значение для величины L:
Lср=

 =337049,1
=337049,1По исходной совокупности опытных данных вычисляется величина

 , характеризующая разброс опытных значений величины x вокруг среднего
, характеризующая разброс опытных значений величины x вокруг среднего 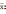
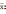
Разброс опытных данных для величины L:
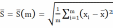
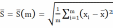 .(7)
.(7)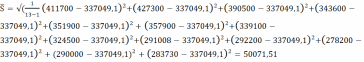
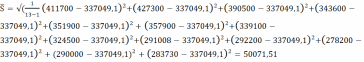

 1,18
1,18
 1,80
1,80-
Рассчитанные значения
 относительно отклонения
относительно отклонения 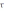
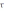 (α;m) сравниваются с его критическими (теоретическими) значениями
(α;m) сравниваются с его критическими (теоретическими) значениями 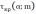
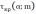 . Так как выборка небольшая (m≤25) для исключения ложных данных используется таблица квантилей распределения максимального относительного отклонения
. Так как выборка небольшая (m≤25) для исключения ложных данных используется таблица квантилей распределения максимального относительного отклонения 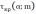
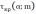 . Значение квантиля максимального относительного отклонения
. Значение квантиля максимального относительного отклонения 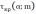
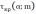 для уровня значимости α=0,05 принимается равным 2,43
для уровня значимости α=0,05 принимается равным 2,43
Таблица 5 - Квантили максимального относительного отклонения
| α, % | Объем выборочной совокупности m | ||||||||
| 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | |
| 1 | 2,37 | 2,46 | 2,54 | 2,61 | 2,66 | 2,71 | 2,76 | 2,8 | 2,84 |
| 5 | 2,17 | 2,24 | 2,29 | 2,34 | 2,39 | 2,43 | 2,46 | 2,49 | 2,52 |
Сравниваются расчетное и критическое значения по формуле:
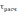
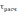 ≤
≤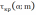
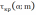 .
.Оба значения
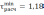
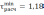 и
и 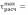
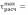 1,80 меньше
1,80 меньше 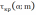
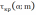 =2,43, следовательно, оба неравенства выполнены и оба значения не считаются ложными и остаются в выборке.
=2,43, следовательно, оба неравенства выполнены и оба значения не считаются ложными и остаются в выборке.Таким образом, рассчитываются оставшиеся выборочные совокупности. Результаты расчетов представлены в таблице
Таблица 6 - Результаты расчетов
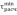
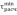 ,
, 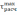
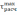 отклонений крайних значений случайных величин
отклонений крайних значений случайных величин
хmin, хmax от среднего значения


| | хmin | хmax | 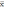 | 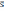 | 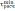 | 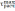 |
| L | 278200 | 427300 | 337049,1 | 50071,51 | 1,18 | 1,80 |
| m1 | 625,00 | 2540,00 | 1412,69 | 633,14 | 1,24 | 1,78 |
| m2 | 10,00 | 51,00 | 27,15 | 13,63 | 1,26 | 1,75 |
| m3 | 15,00 | 65,00 | 43,23 | 16,46 | 1,72 | 1,32 |
| N | 29090,00 | 58420,00 | 42397,23 | 9609,77 | 1,38 | 1,67 |
| Kч | 2,203 | 6,170 | 4,031 | 1,197 | 1,787 | 0,8 |
| Kл | 0,034 | 0,124 | 0,077 | 0,028 | 1,685 | 0,02 |
| Kп.з. | 0,529 | 1,688 | 1,250 | 0,341 | 1,285 | 0,25 |
| Kт | 23,000 | 46,544 | 33,323 | 8,472 | 1,561 | 5,0 |
| S | 1527,60 | 11161,50 | 4712,3 | 3024,73 | 1,05 | 2,13 |
| D | 17,80 | 33,50 | 24,12 | 5,78 | 1,09 | 1,62 |
| E | 10360,00 | 14383,00 | 12226,23 | 1065,65 | 1,75 | 2,02 |
| I | 11,50 | 71,80 | 37,14 | 20,00 | 1,28 | 1,73 |
| V | 65,50 | 404,80 | 202,70 | 108,25 | 1,27 | 1,87 |
| Vp | 41400,00 | 244700,00 | 128953,8 | 66864,25 | 1,31 | 1,73 |
Как видно из таблицы все значения

 и
и 
 выборочных совокупностей удовлетворяют неравенству
выборочных совокупностей удовлетворяют неравенству 
 ≤
≤
 . В результате проведенной процедуры можно утверждать, что в таблице значений случайных величин ложных данных нет.
. В результате проведенной процедуры можно утверждать, что в таблице значений случайных величин ложных данных нет.Проверка опытных данных на их случайность и независимость
При проведении статистического исследования возможны случаи нарушения условий проведения эксперимента, не относящиеся к наличию в выборочной совокупности ложных данных. Случайность и независимость опытных данных – необходимое условие репрезентативности выборочной совокупности.
Наблюдение считается статистически независимым, если результаты, полученные в результате отдельного наблюдения, не связаны с данными предыдущих и последующих наблюдений. Необходимы критерии, которые позволяют установить случайность и независимость данных в выборочной совокупности.
Для статистической проверки случайности и независимости результатов наблюдения применяются:
-
критерий серий, основанный на использовании медианы выборки; -
критерий «восходящих» и «нисходящих» серий.
В данном случае выбрана проверка опытных данных с помощью критерия, основанного на использовании медианы выборки при уровне значимости α=0,05.
Критерий, основанный на использовании медианы выборки, позволяет заметить монотонное смещение среднего выборочного значения в ходе эксперимента.
-
Имеются 13 совокупностей значений случайных величин, прошедшие процедуру исключения ложных данных. В данном случае n=m, так как ни одного значения исключено не было (m – количество значений в выборке, n – число наблюдений, оставшихся после исключения ложных результатов). Совокупности располагаются в порядке возрастания. (Таблица 4) -
Находится выборочное значение медианы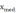
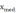 (n) по следующей формуле:
(n) по следующей формуле: