Файл: Обоснование метода математического прогнозирования несчастных случаев и профессиональных заболеваний.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 25.10.2023

Просмотров: 277

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.



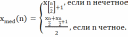
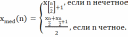
Так как число n=13 является нечетным, то согласно формуле получаем:





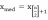
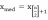
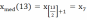
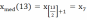
Так для каждого значения выписывается седьмое значение из упорядоченной выборочной совокупности и заносится в таблицу:

Таблица 7 – Значения медианы


Показатели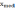


L
339100

m1
1313

m2
28

m3
40

N
40689

Kч
3,872

Kл
0,081

Kп.з.
1,313

Kт
35,826

S
4194,5

d
23,3

e
12314

I
44,5

V
205,8

Vp
134100




  1. В исходной (неупорядоченной) выборке x1, x2, …,xn вместо каждого числа xi ставится «+» (плюс), если xi > xmed(n), и «-» (минус), если

xi< xmed(n). Значениям xi= xmed(n) никакого знака не присваивается.

Таблица 8 - Последовательность

№
L
m1
m2
m3
N
Kч
Kл
Kп.з.

1
+
+
+
+
+
+
+
+

2
+
+
+
+
+
+
+
+

3
+
+
+
+
+
+
+
+

4
+
+



+
+
+



+

5
+
+
+
+



+
+
+

6
+
+
+
+
-
+
+



7






+
-
+



+
-

8
-
-
-
-
+
-
-
-

9
-
-
-
-
-
-
-
-

10
-
-
-



-
-
-
+

11
-
-
-
-
-
-
-
-

12
-
-
-
-
-
-
-
-

13
-
-
-
-
-
-
-
-

№
Kт
S
D
E
I
V
Vp

1
-
-
-
-
-
-
-

2
-
-
-
-
-
-
-

3
-
-
-
-
-
-
-

4
-
-
-
-
-
-
-

5
-
-
-
-
-
-
-

6
-
-
-
-
-
-
-

7





















8
+
+
+
+
-
+
+

9
+
+
+
-
-
+
+

10
+
+
+
+
+
+
+

11
+
+
+
+
+
+
+

12
+
+
+
+
+
+
+

13
+
+
+
+
+
+
+


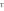
Полученные последовательности плюсов и минусов характеризуются числом серий ν(α;n) и длиной 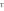(α;n) самой длинной серии. Под серией понимается последовательность идущих подряд плюсов или минусов.

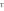
Производится подсчет числа νрасч(n) подряд идущих знаков «+» и подряд идущих знаков «-», а также длина расч(α;n) самой длиной серии плюсов или минусов. Пустые клетки таблицы при подсчетах не учитываются.

Таблица 9 – Значения νрасч и
расч

Показатель
νрасч(n)
расч(n)

L
2
6

m1
2
6

m2
2
6

m3
2
6

N
4
5

Kч
2
6

Kл
2
6

Kп.з.
4
5

Kт
2
6

S
2
6

D
2
6

E
4
6

I
4
6

V
2
6

Vp
2
6




  1. Рассматривается гипотеза о случайности и независимости данных в рассматриваемых выборочных совокупностях (при уровне значимости α=0,05).

В этих предположениях для случайных величин νрасч(n) и расч
(n) проверяется выполнение системы неравенств:



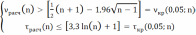
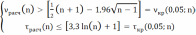
Если хотя бы одно из условий системы окажется невыполненным, то предположение о независимости результатов наблюдения отвергается с вероятностью α=0,05 совершить ошибку первого рода.

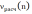
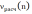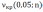
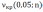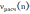
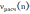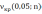
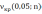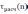
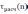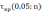
Если ≤ , то есть если расчетное число серий не будет превосходить критическую величину числа серий, то данные исследуемой выборочной совокупности следует признать неслучайными и зависимыми при заданном уровне значимости α=0,05. Это же верно и в случае, если > 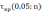, то есть если расчетная длина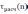 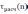самой длинной из серий превосходит критическую величину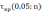 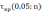, вычисленную по формуле, либо равна ей.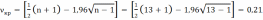





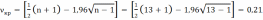
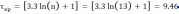
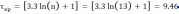
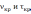
Сравнив полученные результаты 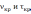с расчетными для всех выборок, напрашивается вывод, что с вероятностью 1-α=1-0,05=0,95 гипотеза о случайности и независимости совокупности исследуемых выборочных значений случайных величин не должна быть отвергнута.

Смотрите также файлы