Файл: Урок алгебры в 11 классе по теме Предел функции в точке. Производная функции в точке. Геометрический и физический смысл производной..doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 114
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
.
Какое правило нужно использовать для нахождения производных функций?
f(x) = 6sinx; f(x) = x5+ 3
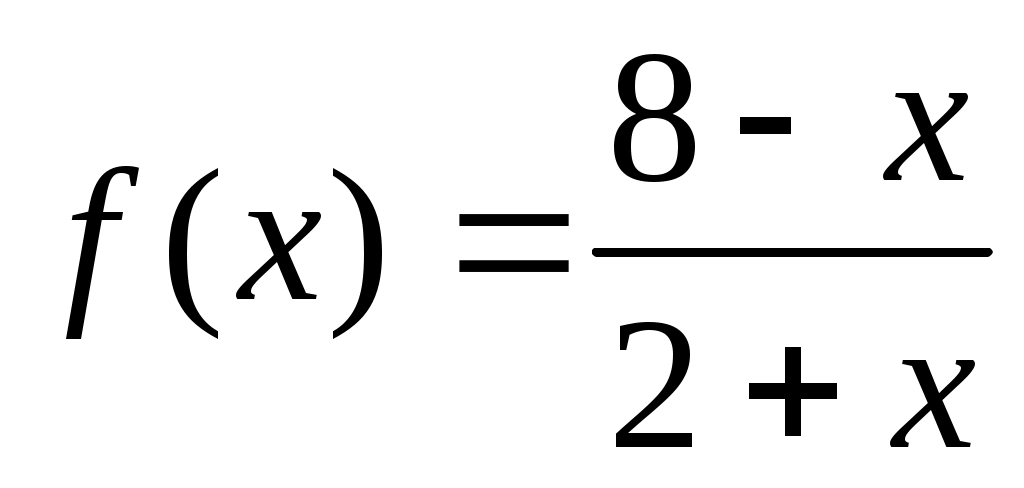
f(x) = 8x4 + 5cosx
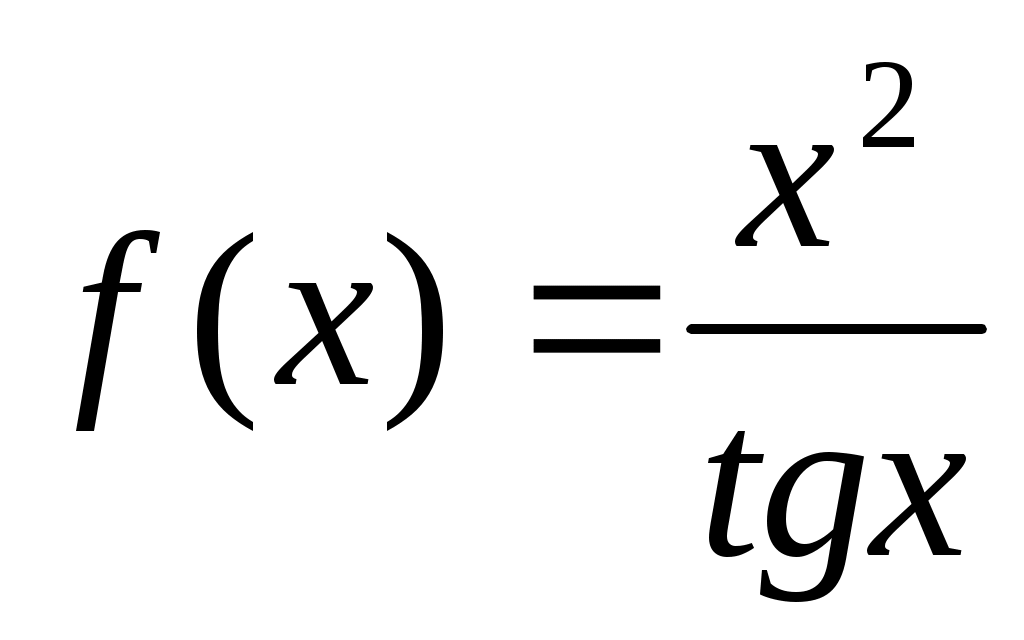 ;
; 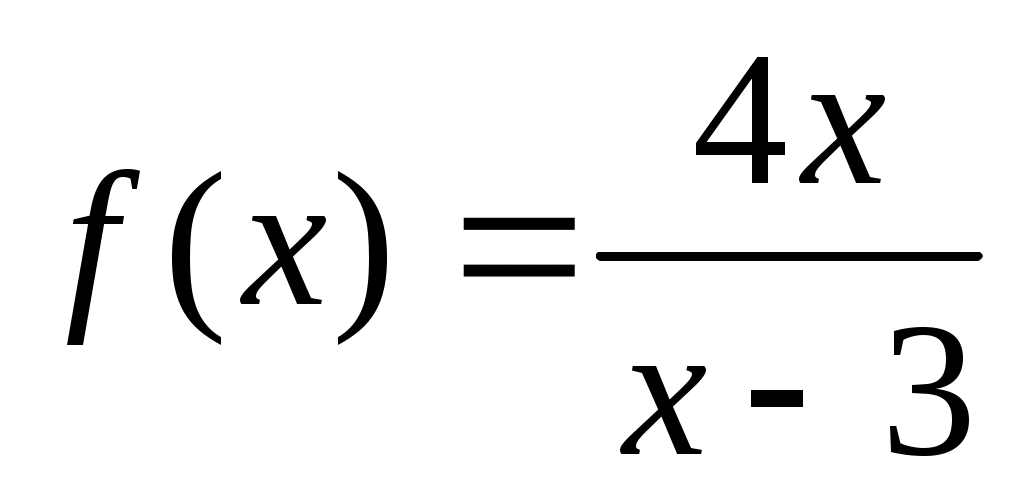 ;
; 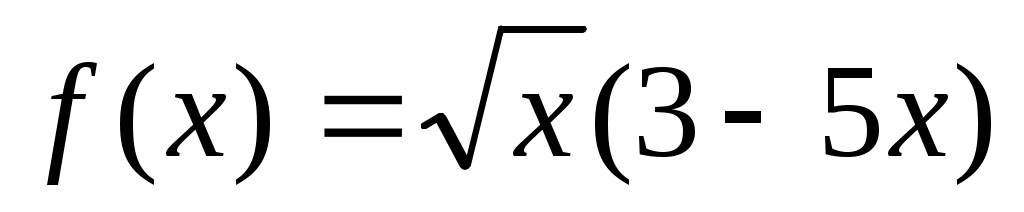
(x) = (2-x)(2+x)
Понятие производная возникло в связи с необходимостью решения ряда задач физики, механики и математики. Честь открытия основных законов математического анализа принадлежит английскому ученому Ньютону и немецкому математику Лейбницу. Лейбниц рассматривал задачу о проведении касательной к произвольной кривой.
З наменитый физик Исаак Ньютон, родившейся в английской деревушке Вульстроп, внес немалый вклад и в математику. Решая задачи на проведение касательных к кривым, вычисляя площади криволинейных ф
наменитый физик Исаак Ньютон, родившейся в английской деревушке Вульстроп, внес немалый вклад и в математику. Решая задачи на проведение касательных к кривым, вычисляя площади криволинейных ф игур, он создал общий метод решения таких задач – метод флюксий (производных), а саму производную называл флюентой.
игур, он создал общий метод решения таких задач – метод флюксий (производных), а саму производную называл флюентой.
Он вычислил производную и интеграл степенной функции. О дифференциальном и интегральном исчислениях он пишет в своей работе «Метод флюксий» (1665 – 1666гг.), послужившей одним из начал математического анализа, дифференциального и интегрального исчисления, которое ученый разработал независимо от Лейбница.
Многие ученые в разные годы интересовались касательной. Эпизодически понятие касательной встречалось в работах итальянского математика Н.Тартальи (ок. 1500 – 1557гг.) – здесь касательная появилась в ходе изучения вопроса об угле наклона орудия, при котором обеспечивается наибольшая данность полета снаряда. И. Кепплер рассматривал касательную в ходе решения задачи о наибольшем объеме параллелепипеда, вписанного в шар данного радиуса.
В 17 веке на основе учения Г.Галилея о движении активно развилась кинематическая концепция производной. Различные варианты изложения встречаются у Р.Декарта, французского математика Роберваля, английского ученого Д.Грегори, в работах И. Барроу.
Вопрос учителя:
Можно ли считать верным утверждение: касательная к графику – это прямая, имеющая с кривой только одну общую точку?
В процессе определения касательной обнаруживают прямую, представляющее собой некое предельное положение секущей, которую и называют касательной к кривой в некоторой точке.
Пусть дана функция y = f (x) и точка М(а; f(a)) и пусть существует призводная f '(а). Уравнение касательной – это уравнение прямой, поэтому оно имеет вид: y = kx + m. Следовательно, задача состоит в том, чтобы отыскать k и m. Из ранее изученного известно, что k = f '(а).
Найдем m. Искомая прямая походит через точку М(а; f(a)), подставим эти координаты в уравнение прямой: f(a) = ka + m, отсюда m = f(a) – ka. Подставим значение m в уравнение
y = kx + m.
y = kx + f(a) – ka,
y = f(a) + f '(а) · (x-a).
Нами получено уравнение касательной к графику функции y = f(x) в точке х = а.
Используя эту формулу, мы можем задать алгоритм составления уравнения касательной к графику функции y = f (x) (предлагаю составить алгоритм самим учащимся):
Решить устно № 491, 504.
1) Составить уравнение касательной к графику функции f(x) = х² - 3х + 5 в точке с абсциссой а = -1.
Решение: Составим уравнение касательной (по алгоритму).
y = 4 – 5x.
Ответ: y = 4 – 5x.
2) Составить уравнение касательной, проходящей через точку пересечения графика функции f(x) = (3 – х)/(х + 1) с прямой y = 1.
Решение: Найдем абсциссу точки касания:
(3 – а)/(а + 1) = 1, а = 1.
Составим уравнение касательной по алгоритму:
y = 2 – х.
Ответ: y = 2 – х.
Решить письменно № 513(а), 514 (а), 561(а), 551(а).
ВАРИАНТ 1
А. Ускорение. Б. Скорость. В. Угловой коэффициент.
2. Точка движется по прямой по закону S(t) = 2t3 + 3t . Чему равна скорость точки в момент времени t = 1?
А. 5. Б. 12. В. 9. Г. 3.
3. Заполните пропуски:
а)( )' = 3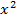 - 4 +
- 4 + 
; б) (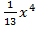 - 25
- 25 -
-  )' = ( ).
)' = ( ).
4. Разбейте на пары «функция - производная».
а)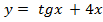 ; 1)
; 1) 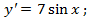
б)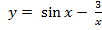 ; 2)
; 2)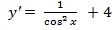 ;
;
в)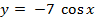 ; 3)
; 3) 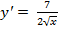

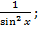
г)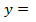 7
7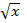 +
+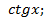 4)
4)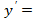
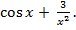
5. Найдите угловой коэффициент касательной, проведённой к графику функции f( )
) 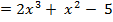 через его точку с абсциссой
через его точку с абсциссой 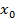
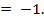
А. 8. Б. 4. В. – 8. Г. – 4.
ВАРИАНТ 2
А. Ускорение. Б. Скорость В. Угловой коэффициент.
2. Точка движется по прямой по закону S(t) = 2t2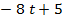 . Вычислите ускорение движения.
. Вычислите ускорение движения.
А. – 4. Б. – 8. В. 4. Г. 8.
3. Заполните пропуски:
а)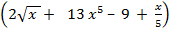 '
' 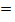 ( ); б) ( )'
( ); б) ( )' 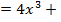

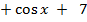 .
.
4. Разбейте на пары «функция - производная».
а)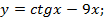 1)
1) 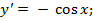
б)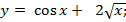 2)
2) 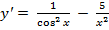
в)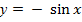 ; 3)
; 3) 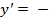
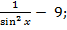
г)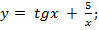 4)
4) 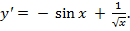
5. Найдите угловой коэффициент касательной, проведённой к графику функции f( )
) 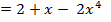 через его точку с абсциссой
через его точку с абсциссой 
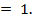
А. - 7. Б. 8. В. 7. Г. 9.
Ответ:
Вариант 1 Вариант 2
б)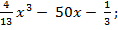 б)
б)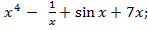
| | c | | |
| n | (c | | |
| ( | | | |
| 2 | 0 | | |
| ( | c' | 1 | |
Какое правило нужно использовать для нахождения производных функций?
f(x) = 6sinx; f(x) = x5+ 3
f(x) = 8x4 + 5cosx
(x) = (2-x)(2+x)
-
Историческая справка
Понятие производная возникло в связи с необходимостью решения ряда задач физики, механики и математики. Честь открытия основных законов математического анализа принадлежит английскому ученому Ньютону и немецкому математику Лейбницу. Лейбниц рассматривал задачу о проведении касательной к произвольной кривой.
З
 наменитый физик Исаак Ньютон, родившейся в английской деревушке Вульстроп, внес немалый вклад и в математику. Решая задачи на проведение касательных к кривым, вычисляя площади криволинейных ф
наменитый физик Исаак Ньютон, родившейся в английской деревушке Вульстроп, внес немалый вклад и в математику. Решая задачи на проведение касательных к кривым, вычисляя площади криволинейных ф игур, он создал общий метод решения таких задач – метод флюксий (производных), а саму производную называл флюентой.
игур, он создал общий метод решения таких задач – метод флюксий (производных), а саму производную называл флюентой.Он вычислил производную и интеграл степенной функции. О дифференциальном и интегральном исчислениях он пишет в своей работе «Метод флюксий» (1665 – 1666гг.), послужившей одним из начал математического анализа, дифференциального и интегрального исчисления, которое ученый разработал независимо от Лейбница.
Многие ученые в разные годы интересовались касательной. Эпизодически понятие касательной встречалось в работах итальянского математика Н.Тартальи (ок. 1500 – 1557гг.) – здесь касательная появилась в ходе изучения вопроса об угле наклона орудия, при котором обеспечивается наибольшая данность полета снаряда. И. Кепплер рассматривал касательную в ходе решения задачи о наибольшем объеме параллелепипеда, вписанного в шар данного радиуса.
В 17 веке на основе учения Г.Галилея о движении активно развилась кинематическая концепция производной. Различные варианты изложения встречаются у Р.Декарта, французского математика Роберваля, английского ученого Д.Грегори, в работах И. Барроу.
-
Изучение нового материала.
Вопрос учителя:
Можно ли считать верным утверждение: касательная к графику – это прямая, имеющая с кривой только одну общую точку?
В процессе определения касательной обнаруживают прямую, представляющее собой некое предельное положение секущей, которую и называют касательной к кривой в некоторой точке.
Пусть дана функция y = f (x) и точка М(а; f(a)) и пусть существует призводная f '(а). Уравнение касательной – это уравнение прямой, поэтому оно имеет вид: y = kx + m. Следовательно, задача состоит в том, чтобы отыскать k и m. Из ранее изученного известно, что k = f '(а).
Найдем m. Искомая прямая походит через точку М(а; f(a)), подставим эти координаты в уравнение прямой: f(a) = ka + m, отсюда m = f(a) – ka. Подставим значение m в уравнение
y = kx + m.
y = kx + f(a) – ka,
y = f(a) + f '(а) · (x-a).
Нами получено уравнение касательной к графику функции y = f(x) в точке х = а.
Используя эту формулу, мы можем задать алгоритм составления уравнения касательной к графику функции y = f (x) (предлагаю составить алгоритм самим учащимся):
-
Обозначим абсциссу точки касания буквой а. -
Вычислим f(a). -
Найдем f '( х) и вычислим f '( а). -
Подставим найденные значения числа а, f( а), f '( а) в уравнение касательной. -
Зарядка для глаз. -
Закрепление нового материала.
Решить устно № 491, 504.
1) Составить уравнение касательной к графику функции f(x) = х² - 3х + 5 в точке с абсциссой а = -1.
Решение: Составим уравнение касательной (по алгоритму).
-
а = -1; -
f(a) = f(-1) = 1 + 3 + 5 = 9; -
f '(x) = 2х – 3,
f '(a) = f '(-1) = -2 – 3 = -5; -
y = 9 – 5 · (x + 1),
y = 4 – 5x.
Ответ: y = 4 – 5x.
2) Составить уравнение касательной, проходящей через точку пересечения графика функции f(x) = (3 – х)/(х + 1) с прямой y = 1.
Решение: Найдем абсциссу точки касания:
(3 – а)/(а + 1) = 1, а = 1.
Составим уравнение касательной по алгоритму:
-
f(a) = f(1) = 1; -
f '(x) = -4/(х +1)²; -
f '(a) = f '(1) = -1; -
y = 1 – 1 · (х – 1),
y = 2 – х.
Ответ: y = 2 – х.
Решить письменно № 513(а), 514 (а), 561(а), 551(а).
-
Самостоятельная работа.
ВАРИАНТ 1
-
В чём состоит физический смысл производной?
А. Ускорение. Б. Скорость. В. Угловой коэффициент.
2. Точка движется по прямой по закону S(t) = 2t3 + 3t . Чему равна скорость точки в момент времени t = 1?
А. 5. Б. 12. В. 9. Г. 3.
3. Заполните пропуски:
а)( )' = 3
; б) (
4. Разбейте на пары «функция - производная».
а)
б)
в)
г)
5. Найдите угловой коэффициент касательной, проведённой к графику функции f(
А. 8. Б. 4. В. – 8. Г. – 4.
ВАРИАНТ 2
-
В чём состоит геометрический смысл производной?
А. Ускорение. Б. Скорость В. Угловой коэффициент.
2. Точка движется по прямой по закону S(t) = 2t2
А. – 4. Б. – 8. В. 4. Г. 8.
3. Заполните пропуски:
а)
4. Разбейте на пары «функция - производная».
а)
б)
в)
г)
5. Найдите угловой коэффициент касательной, проведённой к графику функции f(
А. - 7. Б. 8. В. 7. Г. 9.
Ответ:
Вариант 1 Вариант 2
-
Б; 1. В; -
В; 2. В; -
а)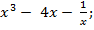 3. а)
3. а) 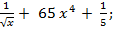
б)