Файл: Методические рекомендации по выполнению курсового проекта по дисциплине Математические модели в экономике.doc

Скачать файл (1,14Мб)

Заказать решение

ВУЗ: Не указан

Категория: Методичка

Дисциплина: Не указана

Добавлен: 25.10.2023

Просмотров: 141

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Петербургский государственный университет путей сообщения

Императора Александра I»

(ФГБОУ ВПО ПГУПС)
Кафедра «Экономика транспорта»

В.Г. Карчик

Методические рекомендации
по выполнению курсового проекта
по дисциплине
«Математические модели в экономике» (Б1.В.ОД.5)
для направления

38.03.01 «Экономика»

по профилю

«Экономика предприятий и организаций (транспорт)»
Форма обучения – очная, заочная

Санкт-Петербург

2016

Методические рекомендации по выполнению курсового проекта по дисциплине «Математические модели в экономике» по направлению 38.03.01 «Экономика» по профилю подготовки «Экономика предприятий и организаций (транспорт)», разработаны доцентом кафедры «Экономика транспорта» к.э.н., доцентом В.Г. Карчиком.
Рассмотрены и утверждены на заседании кафедры
«Экономика транспорта»

Протокол № 4 от « 20 » января 2016 г.

Федеральное агентство железнодорожного транспорта

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ПУТЕЙ СООБЩЕНИЯ Императора Александра I»
(ФГБОУ ВПО ПГУПС)
Кафедра «Экономика транспорта»

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
ЭКОНОМИЧЕСКИХ ПРОЦЕССОВ
НА ЖЕЛЕЗНОДОРОЖНОМ ТРАНСПОРТЕ

Методические указания и задания к курсовому проекту

Санкт-Петербург

2016

Федеральное агентство железнодорожного транспорта

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ПУТЕЙ СООБЩЕНИЯ Императора Александра I»
(ФГБОУ ВПО ПГУПС)
Кафедра «Экономика транспорта»

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
ЭКОНОМИЧЕСКИХ ПРОЦЕССОВ
НА ЖЕЛЕЗНОДОРОЖНОМ ТРАНСПОРТЕ

Методические указания и задания к курсовому проекту

Санкт-Петербург

2016

УДК 385

ББК 65.37

М34

М

М34
атематическое моделирование экономических процессов на железнодорожном транспорте : метод. указания и задания к курсовому проекту / В. Г. Карчик, Б. П. Немцов. – СПб. : ФГБОУ ВПО ПГУПС, 2016. – 34 с.
Курсовой проект по дисциплине «Математические модели в экономике» состоит из трех частей. В первой части студентам предлагается решить транспортную задачу в матричной и сетевой формах и обобщённую транспортную задачу. Во второй части рассматриваются вопросы применения методов математической статистики в экономических расчетах. В третьей части предлагается решить общую задачу линейного программирования с помощью симплекс-метода и его модификаций. На основе полученных результатов предусматривается углубленный анализ производственных программ, в том числе эффективность и состояние использованных ресурсов, получаемой при этом прибыли. Для большинства задач предлагается алгоритм решения и рассматриваются конкретные численные примеры.

Методические указания и задания к выполнению курсового проекта предназначены для студентов бакалавриата, изучающих дисциплину «Математические модели в экономике» по направлению «Экономика», профилям «Экономика предприятий и организаций (транспорт)», «Бухгалтерский учет, анализ и аудит».
УДК 385

ББК 65.37

© ФГБОУ ВПО ПГУПС, 2016
1 Использование методов линейного программирования
для целей оптимального распределения ресурсов
1.1 Оптимизация плана перевозок
с использованием метода потенциалов
1. Составить допустимый план транспортной задачи, используя метод минимальной стоимости для построения базисного плана с ограничением пропускной способности.

2. Определить оптимальный план транспортной задачи, используя метод потенциалов. Построенный допустимый и оптимальный план должен удовлетворять условиям постановки транспортной задачи:

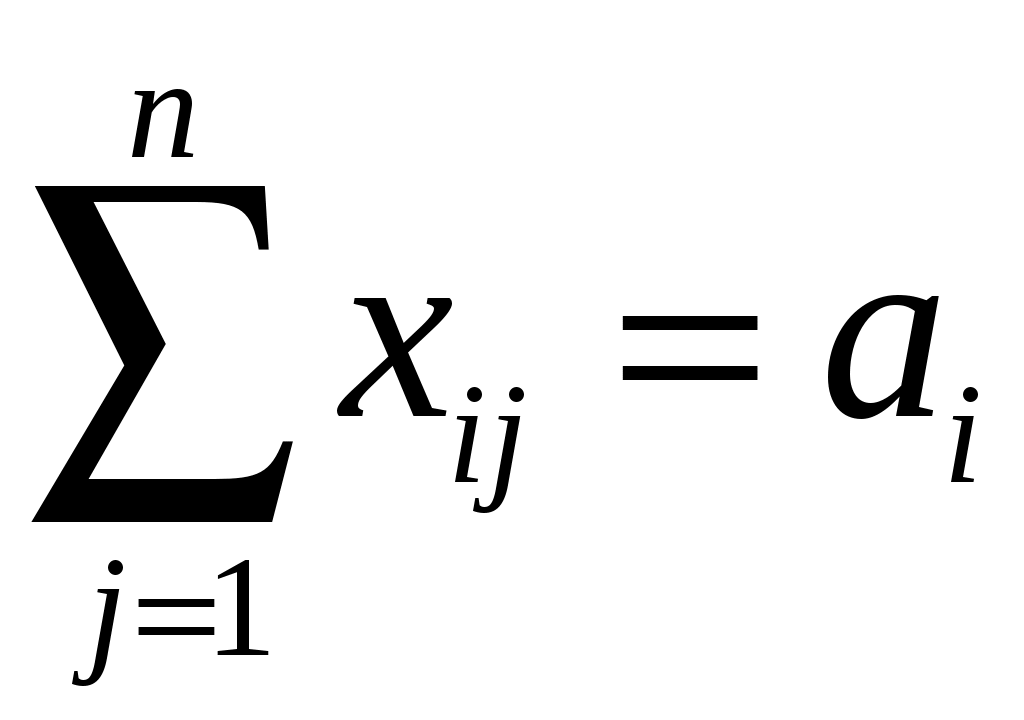, i = 1, 2, 3, …, m; (1.1)

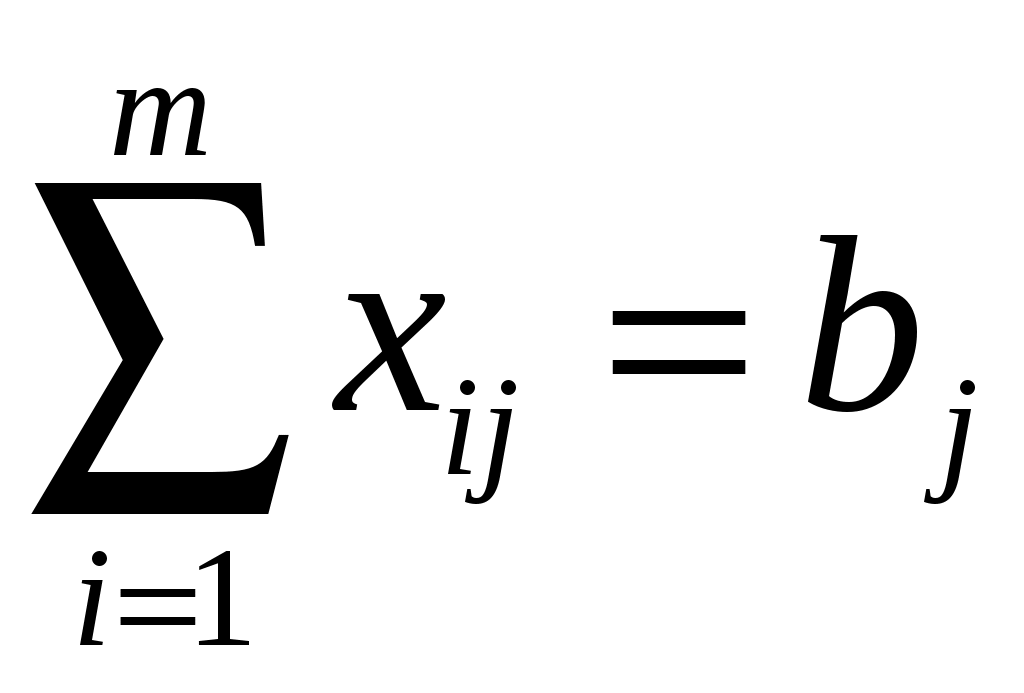, j = 1, 2, 3, …, n; (1.2)

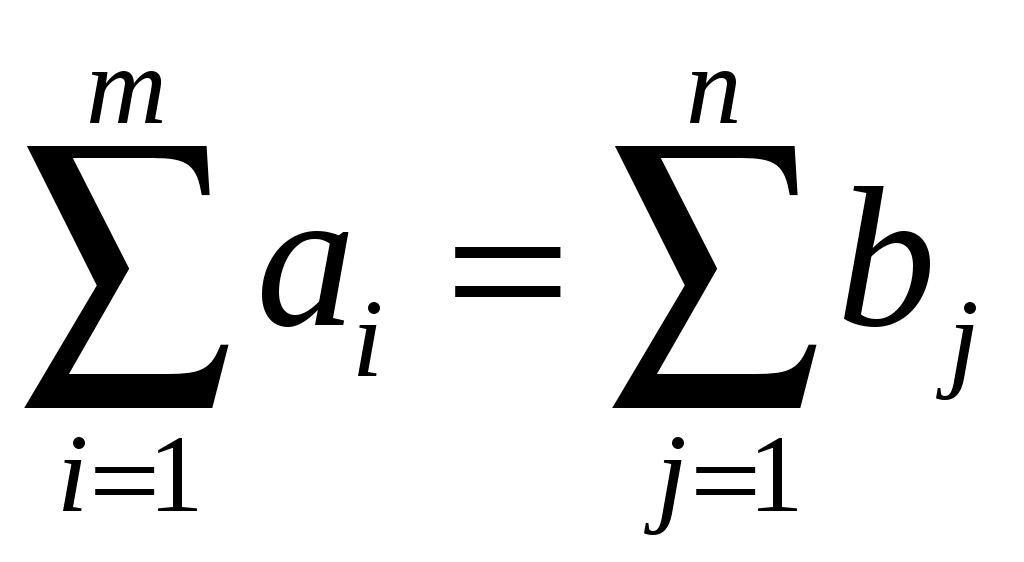; (1.3)

. (1.4)
Целевая функция задачи:

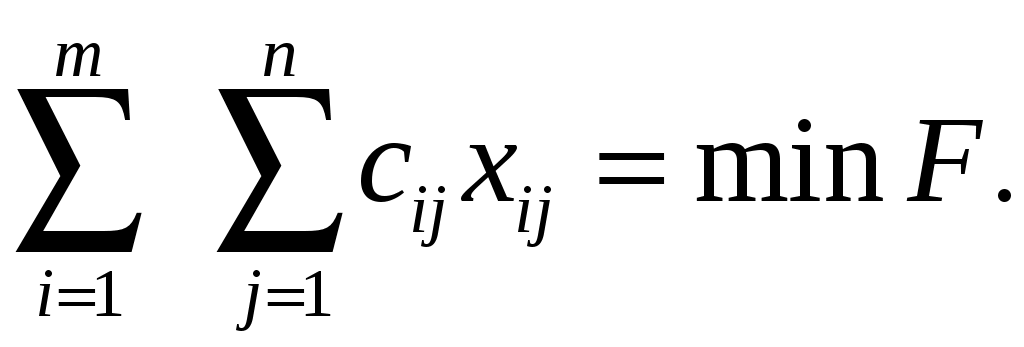(1.5)
3. Рассчитать целевые функции каждого базисного плана перевозок.

4. Найти экономический эффект от оптимизации. Экономический эффект от оптимизации рассчитывается как разность между целевыми функциями базисного и оптимального планов.

5. Рассчитать матрицу показателей характеристик оптимального плана перевозок транспортной задачи. Характеристики для клеток матрицы рассчитываются по формуле:
D_ij = c_ij – (V_j – U_i). (1.6)

6. Показать варианты альтернативных решений при одной и той же целевой функции или при минимальных от нее отклонениях.
Исходные данные приведены по вариантам в табл. 1.1–1.3. В табл. 1.1 приведена матрица стоимости перевозок для всех вариантов (с_ij), где в пяти клетках справа записаны величины d_ij, ограничивающие пропускную способность. В табл. 1.2 приведены данные по ресурсам поставщиков (a_i) – первая цифра номера варианта; в табл. 1.3 приведены данные по спросу потребителей (b_j) – вторая цифра номера варианта.
Таблица 1.1

10	20 35	75	160	90	80	70	60	a₁
10	30	45	40	25	65	30	10 30	a₂
15	10	10 25	20	25	80	20	85	a₃
45	8 20	35	30	110	40	75	20	a₄
80	40	90	105	150	50	30 25	90	a₅
b₁	b₂	b₃	b₄	b₅	b₆	b₇	b₈

Таблица 1.2

	1	2	3	4	5	6	7	8	9	0
a₁	150	150	150	145	155	400	400	150	400	145
a₂	150	145	150	155	150	155	150	155	155	400
a₃	145	155	155	150	400	145	150	150	150	150
a₄	155	400	145	150	150	150	155	145	150	150
a₅	400	150	400	400	145	150	145	400	145	155

Таблица 1.3

	1	2	3	4	5	6	7	8	9	0
b₁	150	150	150	100	150	150	150	150	150	100
b₂	100	100	150	100	100	100	100	100	150	100
b₃	100	150	100	150	100	100	100	150	150	100
b₄	100	100	100	100	150	100	100	150	150	100
b₅	100	100	100	100	100	150	150	150	100	150
b₆	150	150	100	150	150	150	100	100	100	150
b₇	150	100	150	150	150	100	150	100	100	150
b₈	150	150	150	150	100	150	150	100	100	150

1.2 Оптимизация плана транспортной задачи
с использованием метода потенциалов на сети
1. Оптимизировать план перевозок, используя метод потенциалов.

2. Рассчитать целевую функцию оптимального плана перевозок и установить эффект от оптимизации.

3. Для небазисных звеньев с ограничением провозной способности рассчитать прокатные оценки.

Исходные данные приведены на рис. 1.1, в табл. 1.4 и 1.5.

На рис. 1.1 показан полигон железной дороги, где указаны наименования поставщиков, потребителей и значения затрат на доставку. В табл. 1.4 приведены данные по ресурсам поставщиков (a_i) – первая цифра номера варианта. В табл. 1.5 приведены данные по потребителям (b_j) – вторая цифра номера варианта. По некоторым участкам введены ограничения провозной способности: AN = 20; CL = 20; CD = 40; EM = 50.

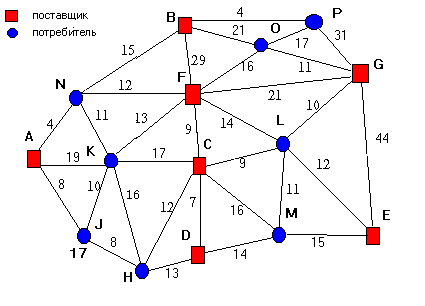
Рис. 1.1. Полигон железной дороги

Таблица 1.4

	1	2	3	4	5	6	7	8	9	0
A	95	60	70	70	56	94	80	60	70	19
B	70	90	80	90	90	70	70	80	138	43
C	80	146	90	138	60	60	19	70	90	80
D	90	70	146	60	80	90	43	19	60	90
E	80	80	60	80	70	80	90	138	43	70
F	19	23	31	43	121	17	138	90	19	60
G	66	31	23	19	23	89	60	43	80	138

Таблица 1.5

	1	2	3	4	5	6	7	8	9	0
H	58	90	86	49	17	89	48	16	42	95
J	77	70	43	31	89	55	87	65	114	33
K	53	43	87	87	67	86	33	114	65	87
L	75	68	67	87	89	78	95	42	16	48
M	67	67	89	67	84	57	42	95	48	16
N	89	55	50	47	40	42	114	33	87	65
O	35	54	37	58	49	58	65	87	33	114
P	46	53	41	74	65	35	16	48	95	42

1.3 Обобщенная транспортная задача
Имеется возможность выпуска пяти видов продукции (j = 1, …, 5) на трех типах оборудования (i = 1, 2, 3).

1. Сформировать математическое описание задачи.

2. Построить первоначальное распределение.

3. Определить оптимальный план модифицированным методом потенциалов.

4. Выполнить анализ оптимального производственного плана, включая состав и объем выпуска продукции и состояние использованных ресурсов.

5. Проанализировать возможность изменения оптимального плана.

Исходные данные приведены в табл. 1.6–1.8. В табл. 1.6 приведены данные по ресурсам оборудования – первая цифра шифра варианта. В табл. 1.7 приведены данные по потребности выпуска продукции – вторая цифра шифра варианта. В табл. 1.8 приведены показатели производительности (Пр) машин и себестоимость (С/с) выпуска продукции – общие для всех вариантов.
Таблица 1.6

Вариант	1	2	3	4	5	6	7	8	9	0
i = 1	300	215	110	125	200	280	180	220	150	300
i = 2	100	120	125	285	100	120	280	180	250	200
i = 3	200	250	280	200	270	275	90	180	200	100

Таблица 1.7

Вариант	1	2	3	4	5	6	7	8	9	0
j = 1	350	150	150	100	350	100	350	150	100	200
j = 2	150	150	150	150	100	150	150	350	350	100
j = 3	150	100	150	150	150	150	100	150	150	300
j = 4	100	150	100	300	150	150	150	150	150	150
j = 5	150	300	300	150	150	300	150	100	150	200

Смотрите также файлы

Транспортная логистика (часть 11) Кокурин Д. И.pdf

Практическая работа Задание.docx

Кафедра доклад по дисциплине Тема Синектика Студент(ка) Козлова Ангелина Юрьевна Л112211 группы.docx

Функция Назначение.docx

Баллов 1 из Отметить вопрос.pdf

Файл: Методические рекомендации по выполнению курсового проекта по дисциплине Математические модели в экономике.doc

Смотрите также файлы

Информация

Списки файлов

Дополнительно

	1	2	3	4	5	6	7	8	9	0
A	95	60	70	70	56	94	80	60	70	19
B	70	90	80	90	90	70	70	80	138	43
C	80	146	90	138	60	60	19	70	90	80
D	90	70	146	60	80	90	43	19	60	90
E	80	80	60	80	70	80	90	138	43	70
F	19	23	31	43	121	17	138	90	19	60
G	66	31	23	19	23	89	60	43	80	138

	1	2	3	4	5	6	7	8	9	0
H	58	90	86	49	17	89	48	16	42	95
J	77	70	43	31	89	55	87	65	114	33
K	53	43	87	87	67	86	33	114	65	87
L	75	68	67	87	89	78	95	42	16	48
M	67	67	89	67	84	57	42	95	48	16
N	89	55	50	47	40	42	114	33	87	65
O	35	54	37	58	49	58	65	87	33	114
P	46	53	41	74	65	35	16	48	95	42

	1	2	3	4	5	6	7	8	9	0
A	95	60	70	70	56	94	80	60	70	19
B	70	90	80	90	90	70	70	80	138	43
C	80	146	90	138	60	60	19	70	90	80
D	90	70	146	60	80	90	43	19	60	90
E	80	80	60	80	70	80	90	138	43	70
F	19	23	31	43	121	17	138	90	19	60
G	66	31	23	19	23	89	60	43	80	138

	1	2	3	4	5	6	7	8	9	0
H	58	90	86	49	17	89	48	16	42	95
J	77	70	43	31	89	55	87	65	114	33
K	53	43	87	87	67	86	33	114	65	87
L	75	68	67	87	89	78	95	42	16	48
M	67	67	89	67	84	57	42	95	48	16
N	89	55	50	47	40	42	114	33	87	65
O	35	54	37	58	49	58	65	87	33	114
P	46	53	41	74	65	35	16	48	95	42

	1	2	3	4	5	6	7	8	9	0
A	95	60	70	70	56	94	80	60	70	19
B	70	90	80	90	90	70	70	80	138	43
C	80	146	90	138	60	60	19	70	90	80
D	90	70	146	60	80	90	43	19	60	90
E	80	80	60	80	70	80	90	138	43	70
F	19	23	31	43	121	17	138	90	19	60
G	66	31	23	19	23	89	60	43	80	138

	1	2	3	4	5	6	7	8	9	0
H	58	90	86	49	17	89	48	16	42	95
J	77	70	43	31	89	55	87	65	114	33
K	53	43	87	87	67	86	33	114	65	87
L	75	68	67	87	89	78	95	42	16	48
M	67	67	89	67	84	57	42	95	48	16
N	89	55	50	47	40	42	114	33	87	65
O	35	54	37	58	49	58	65	87	33	114
P	46	53	41	74	65	35	16	48	95	42