Файл: Методические рекомендации по выполнению курсового проекта по дисциплине Математические модели в экономике.doc

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Методичка

Дисциплина: Не указана

Добавлен: 25.10.2023

Просмотров: 136

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.


Шаги 2, 3. Получен оптимальный план.

2 Применение методов математической статистики
в экономических расчетах
2.1 Расчет параметров регрессионных моделей.
Проверка надежности найденных статистических показателей
и вариаций изменений
Одной из главных задач повышения качества планирования является установление достоверных показателей на основе объективных количественных закономерностей, существующих в экономических процессах на транспорте.

Функциональная зависимость между независимой переменной X и зависимой Y состоит в том, что каждому значению X поставлено в однозначное соответствие определенное значение Y. В реальных условиях, когда одновременно действует много факторов, изучаемая связь теряет свою функциональность. Возникает потребность в оценке таких зависимостей иными, статистическими методами.

Одним из признанных методов определения статистической связи являются расчеты на базе линейной модели регрессионного анализа.

Парную регрессионную модель можно представить в виде графика, где на оси абсцисс откладывается независимая переменная Х, а на оси ординат – зависимая Y. Линейная регрессия описывается уравнением вида
Yx = a + bx,
где Yx – оцениваемая величина;

х – независимая переменная;

a и b – параметры выборки.

В основе расчета параметров лежит метод наименьших квадратов с использованием в качестве математической модели нормальной системы уравнений:

Параметры a и b отыскиваются в ходе соответствующих алгебраических преобразований и подстановки:

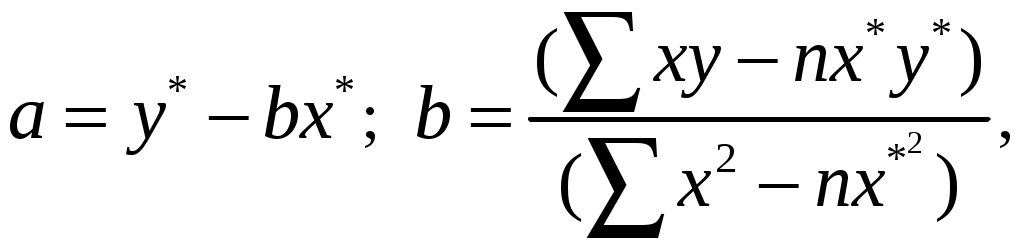
где x*, y* – средние значения параметров, n – число испытаний.

В табл. 2.1 показана последовательность действий при построении уравнения регрессии. В последних двух строках приведены значения сумм и средних показателей. В результате применения формул имеем: b = 2,056, a = 2,333 и уравнение регрессии: Yx = 2,333 + 2,056x.
Задание 2.1. Установить статистическую зависимость между годовым объемом работы по грузообороту (млрд ткм), приняв его за независимую переменную (
x), и фондоемкостью перевозок, приняв ее за зависимую переменную (Y). Составить линейную модель вида Yx = a + bx. Исходные данные по вариантам приведены в табл. 2.2 (грузооборот, млрд ткм (х)) и 2.3 (показатели фондоемкости перевозок (y), руб. на 1 ткм).

Таблица 2.1


n
x
y
xy
x2
Yx
y – Yx
(y – Yx)2
y2
(y – y*)
(y – y*)2

1
5
12
60
25
12,61
–0,611
0,373
144
3,5
12,25

2
4
11
44
16
10,56
0,444
0,197
121
2,5
6,25

3
3
9
27
9
8,5
0,5
0,25
81
0,5
0,25

4
2
8
16
4
6,444
1,555
2,419
64
–0,5
0,25

5
1
4
4
1
4,389
–0,388
0,151
16
–4,5
20,25

6
3
10
30
9
8,5
1,5
2,25
100
1,5
2,25

7
2
6
12
4
6,444
–0,444
0,199
36
–2,5
6,25

8
2
7
14
4
6,444
0,555
0,308
49
–1,5
2,25

9
2
5
10
4
6,444
–1,444
2,089
25
–3,5
12,25

10
4
10
40
16
10,56
–0,555
0,308
100
1,5
2,25

11
5
13
65
25
12,61
0,388
0,154
169
4,5
20,25

12
3
7
21
9
8,5
–1,5
2,25
49
–1,5
2,25

∑
36
102
343
126






10,944
954



87

x* = 3
y* = 8,5


Таблица 2.2

1
2
3
4
5
6
7
8
9
0

10
9
11
13
14
13
13
13
11
13

11
11
11
11
11
11
9
8
9
10

9
9
9
9
9
8
8
8
8
9

8
8
8
8
8
8
8
8
8
8

4
4
4
4
4
4
4
4
4
4

10
10
10
10
10
10
10
10
10
10

6
6
6
6
6
6
6
6
7
6

7
7
7
7
7
7
7
7
6
7

5
5
5
5
5
5
5
5
5
5

10
10
10
10
10
10
10
10
13
10

13
13
13
13
13
13
13
13
10
13

7
7
7
7
7
7
7
7
7
7



Таблица 2.3

1
2
3
4
5
6
7
8
9
0

80
100
100
100
100
100
100
100
100
100

80
100
80
80
80
80
80
80
80
80

60
60
80
60
60
60
60
60
60
60

40
40
40
60
40
40
40
40
40
40

20
20
20
20
40
20
20
20
20
40

60
60
60
60
60
20
60
60
60
60

40
40
40
40
40
40
60
40
40
40

40
40
40
40
40
40
40
60
40
60

40
40
40
40
40
40
40
40
20
40

80
80
80
80
80
80
80
80
80
80

100
100
100
100
100
100
100
100
100
100

60
60
60
60
60
60
60
60
60
60

Задание 2.2. Определить достоверность найденного уравнения линейной регрессионной модели, используя критерий Фишера.

Для использования критерия Фишера (F) устанавливается отношение (η) полной дисперсии ( ) к остаточной ( ):
;
;
,
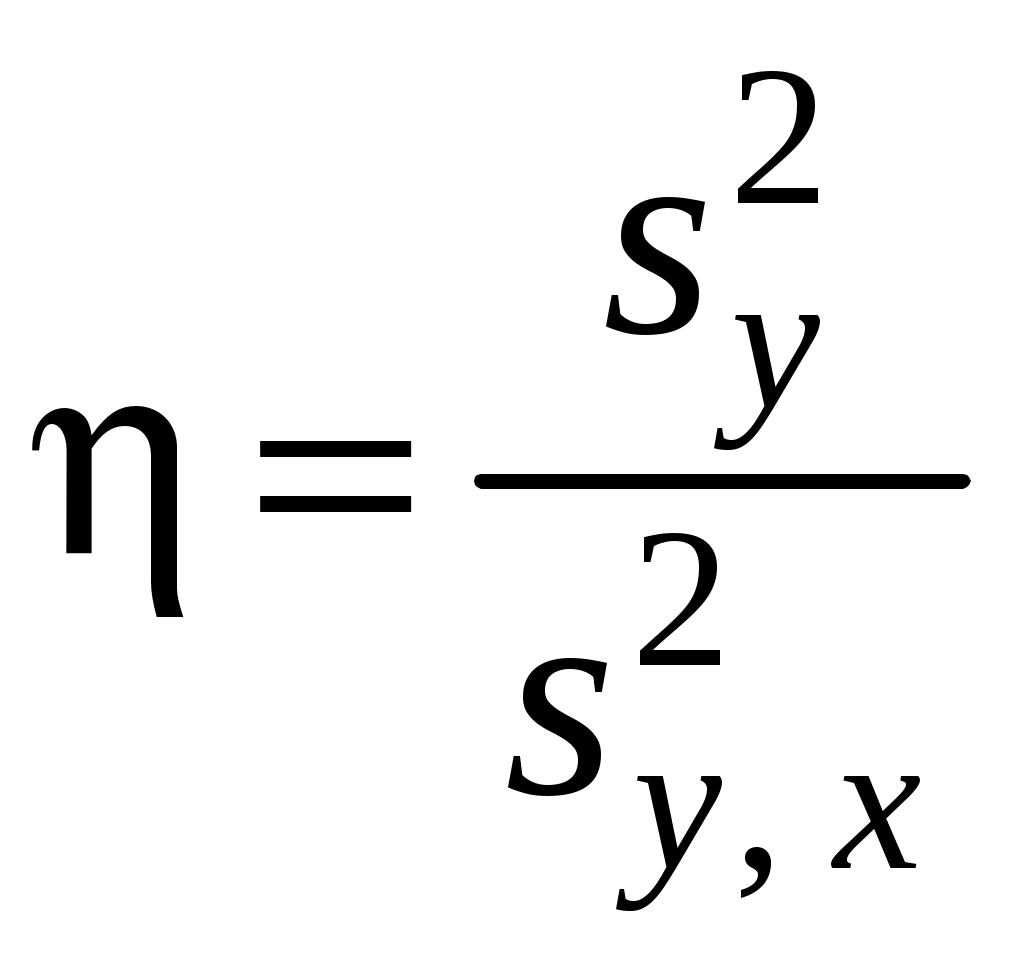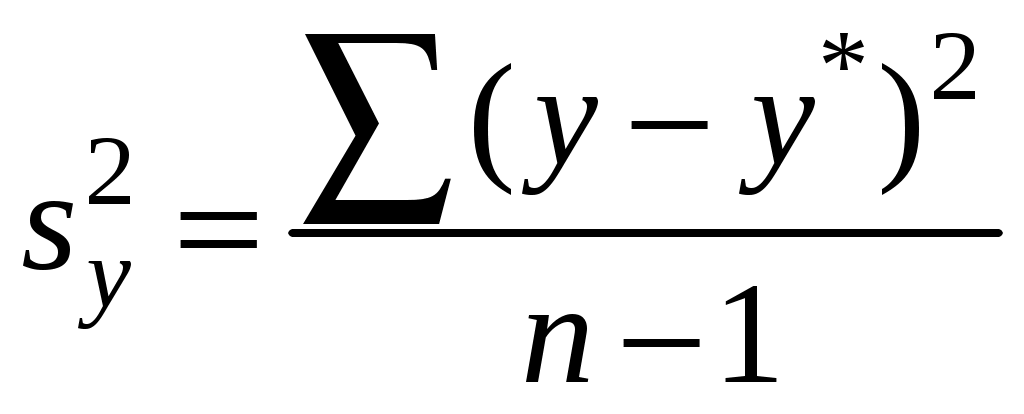где m – число факторов в модели (m = 1).

Из расчетов табл. 2.1 имеем:
∑(y – Yx)2 = 10,94;
∑(y – y*)2 = 87;
= 10,94 / (12 – 2) = 1,094;
= 87 / (12 – 1) = 7,909.
Найдем теперь отношение η = 7,909 / 1,094 = 7,23.

По соответствующей статистической таблице F-распределения (приложение, табл. П1) определим, что с доверительной вероятностью, например в 95 случаях из 100, мы имеем удовлетворительный результат, так как f(0,95) = 2,94 и меньше значения η. Полученный результат позволит нам использовать рассчитанное уравнение регрессии для различных целей, включая прогнозирование.

2.2 Расчет параметров парной корреляции
В основе расчета коэффициента корреляции и параметров оценки его надежности лежит метод наименьших квадратов с использованием в качестве математической модели нормальной системы уравнений линейной регрессии. Найденный коэффициент корреляции показывает уровень тесноты связи между исследуемыми факторами. Чем выше значение коэффициента корреляции, тем теснее исследуемая связь. Расчет линейного коэффициента корреляции выполняется по формуле:

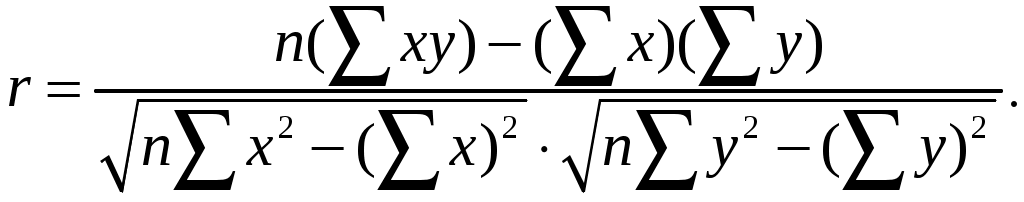
Величина линейного коэффициента корреляции изменяется в диапазоне от –1 до +1. По данным табл. 2.1 находим показатели, необходимые для расчета r. Подставляя их значения в формулу, имеем:

Смотрите также файлы